Жданов Явления переноса в газах и плазме 2008

Уравнение (3.74') называют вторым законом Фика.

Аналогичные уравнения могут быть получены и при использовании массового диффузионного потока J1 . Используя соотношение

(3.66), имеем

Выражая градиент x1 через градиент c1 с помощью (3.63), приходим к соотношению

которое аналогично первому закону Фика (3.70), но записывается в массовых, а не в молярных переменных. Если подставить теперь

J1 в уравнение непрерывности в форме (3.34) и исключить из него производную ∂ ρ∂ t с помощью уравнения непрерывности для смеси в целом (3.35), то приходим к уравнению

с тем же самым коэффициентом бинарной диффузии D12 . Здесь

для простоты предполагается, что u = 0 . Уравнение (3.77) имеет, очевидно, ту же форму, что и уравнение (3.74'), но записывается в

других переменных ( c1 вместо x1 ).

Заметим, что уравнения (3.77) и (3.74'), как и уравнение теплопроводности (3.32), относятся к уравнениям параболического типа. Используя аналогию с результатами, описывающими выравнивание температуры в газе, можно утверждать, что изменение концентрации в газовой смеси, занимающей объем, характерный размер которого равен L , происходит по тому же закону. Это означает, что порядок величины времени τ , в течение которого произойдет заметное выравнивание концентрации в различных точках этого объема, равен

101

т.е. время τD , которое можно назвать временем релаксации для

процесса диффузии, пропорционально квадрату характерного размера задачи и обратно пропорционально коэффициенту диффузии в газовой смеси.

3.6. Тепловой поток в газовой смеси

Как уже отмечалось, выражение для теплового потока q в слу-

чае смеси имеет более сложную структуру, чем в случае простого газа. Вклад в него, связанный с наличием градиента температуры, можно по аналогии с (3.29) представить как

где теплопроводность смеси κ равна сумме парциальных теплопроводностей компонентов

В общем случае, однако, вектор теплового потока содержит члены, зависящие также от диффузионных скоростей компонентов смеси. Один из этих вкладов возникает из-за выбора системы отсчета, в которой рассматривается перенос тепла. В соответствии с общим определением теплового потока (3.48) и парциальных тепловых потоков(3.49) скорости молекул, от которых зависит функция распределения, определены относительно среднемассовой скорости смеси u . Однако перенос тепла через некоторую поверхность в газовой смеси, вызванный неоднородностью температуры, рассматривается обычно в условиях, когда число молекул, пересекающих единичную поверхность в единицу времени с той и другой стороны, одинаково. Это означает, что эта часть теплового потока должна определяться относительно системы отсчета, движущейся

со среднемолярной скоростью смеси u m . Для того чтобы определять тепловые потоки относительно одной выбранной системы отсчета, необходимо установить связь между различными представлениями потоков.

102

Будем исходить из следующего общего определения величин, усредненных на функции распределения,

Fα = n1α ∫Fα fαdvα .

Определяя парциальный тепловой поток компонента α относи-

тельно среднемолярной скорости смеси, имеем

Преобразуем выражение (3.81), полагая, что u мало и поэтому можно пренебречь квадратичными относительно этой величины членами. В результате (3.81) принимает вид

Первый член справа есть обычный вектор парциального теплового потока qα , определяемый в системе отсчета, движущейся со скоростью u . Величину cαcα можно с хорошим приближением заменить средним значением cαcα0 , вычисляемым на максвел-

ловской функции распределения, т.е. c α c α 0 = p α I . На-

конец, коэффициент перед u в последнем члене в соответствии с определением средней энергии частиц сорта α в единице объема газа равен (32)pα . В итоге имеем

В результате

103

α

Фактически это означает, что при таком определении теплового потока в смеси газов дополнительно к обычному переносу тепла за счет градиента температуры возникает перенос, связанный с диффузией компонентов смеси, причем каждая молекула несет в среднем (52)kT тепловой энергии. Выражение (3.84) справедливо, во-

обще говоря, для газовой смеси одноатомных газов. При наличии у молекул внутренних степеней свободы соответствующее обобщение рассмотренного выше вывода приводит к результату

гдеεα определено выражением (1.80).

Еще один вклад в тепловой поток, следующий из известных результатов неравновесной термодинамики [9] и строгой кинетической теории [10,11], оказывается перекрестным по отношению к термодиффузионному вкладу в выражении для диффузионного потока. В частности, для бинарной газовой смеси окончательное выражение для теплового потока принимает вид [11].

где kT – термодиффузионное отношение, которое уже вводилось

нами при определении диффузионного потока (3.71). То обстоятельство, что коэффициент при градиенте температуры в выражении для диффузионного потока и коэффициент при разности диффузионных скоростей в выражении для теплового потока пропорциональны одному и тому же кинетическому коэффициенту kT ,

оказывается прямым следствием выполнения известных соотношений симметрии Онзагера. Эти соотношения являются одним из важных исходных положений неравновесной термодинамики [9].

104

ГЛАВА 4. СТОЛКНОВЕНИЯ ЧАСТИЦ В ГАЗЕ И ПЛАЗМЕ

Условия идеальности газа и плазмы предполагают, что основную часть времени составляющие их частицы проводят в свободном движении и взаимодействуют лишь в короткие моменты их сближения (столкновения). При описании столкновений нейтральных частиц между собой и заряженных частиц с нейтральными это соответствует возможности рассматривать лишь парные соударения частиц, когда взаимодействие с другими окружающими частицами не влияет на характер столкновения выбранной пары. Для взаимодействия заряженных частиц в плазме, которое является дальнодействующим, концепция парного столкновения может быть введена лишь с известными допущениями. Этот вопрос мы обсудим ниже в соответствующем параграфе настоящей главы.

Столкновения частиц в газе и плазме играют решающую роль в установлении равновесных распределений частиц по их скоростям и внутренним состояниям. В обычном одноатомном газе оказываются существенными лишь упругие столкновения атомов, в результате которых скорости их движения меняются как по величине, так и по направлению, но суммарные импульс и кинетическая энергия пары взаимодействующих частиц при этом сохраняются. Следствием этого является установление равновесного максвелловского распределения частиц по скоростям. В газе, образованном из двухатомных и многоатомных молекул, наряду с изменением скорости частиц происходят изменения внутреннего состояния молекул, обусловленные наличием у них вращательных и колебательных степеней свободы. В этом случае наряду с упругими имеют место неупругие столкновения частиц, сопровождающиеся переходом части поступательной энергии молекул в энергию их внутреннего движения. Равновесному состоянию такого газа соответствует

максвелл-больцмановское распределение по скоростям и внутрен-

ним энергиям молекул, которое рассматривалось нами в главе 1. В результате химических реакций (например, диссоциации молекул) в дополнение к рассмотренным эффектам может изменяться распределение частиц по сортам. Столкновения частиц в этом случае являются существенно неупругими.

Элементарные процессы в плазме, соответствующие упругим и неупругим столкновениям с участием атомов, молекул, ионов и

105

электронов, а также фотонов, оказываются гораздо более многообразными, чем в обычном газе. Многие из этих процессов (особенно неупругие столкновения) определяют характер равновесных и неравновесных распределений связанных и свободных частиц плазмы. Именно неупругими столкновениями частиц в плазме определяются такие процессы как возбуждение и девозбуждение атомов и молекул, ионизация и рекомбинация, ионно-молекулярные реакции и т.п..

При анализе явлений переноса в газах и плазме основное внимание уделяется рассмотрению упругих столкновений частиц. Это связано с тем, что именно упругие столкновения вносят основной вклад в определение эффективных сечений рассеяния частиц и характерных макроскопических частот столкновений, которыми и определяются в конечном счете значения коэффициентов переноса. Поэтому ниже рассматривается динамика упругих атом-атомных и ион-атомных столкновений, а также кулоновских столкновений заряженных частиц (электронов и ионов). Ко всем этим случаям (за исключением случая резонансной перезарядки иона на собственном атоме) оказываются полностью применимыми классические методы расчета соответствующих сечений рассеяния. Для процессов столкновений частиц с участием молекул вклад неупругих процессов в суммарное сечение рассеяния часто оказывается малым по сравнению с упругими столкновениями, поэтому в ряде случаев к их описанию также оказываются приближенно применимыми рассматриваемые ниже результаты. Конкретные ситуации, где учет неупругих процессов при столкновении молекул оказывается важным, будут оговорены позднее.

При анализе электронных свойств переноса в слабоионизованной плазме особую роль играют сечения электрон-атомных и электронмолекулярных столкновений. Хотя общие уравнения сохранения импульса и энергии при столкновениях частиц оказываются справедливыми и в этом случае, расчет соответствующих сечений рассеяния возможен лишь на основе квантово-механического рассмотрения. Другой способ состоит в использовании экспериментально определяемых зависимостей эффективных сечений рассеяния электронов на атомах и молекулах от энергии налетающего электрона.

106

4.1. Динамика упругого парного столкновения частиц

Общие закономерности упругого столкновения частиц могут быть рассмотрены на основе законов сохранения импульса и энергии системы частиц без учета конкретного вида взаимодействия между ними. Для парного столкновения частиц разного сорта с

массами m1 и m2 соответствующие законы сохранения записываются в виде

где штрихом отмечены значения скоростей после столкновения. При этом понятия “до” и “после” столкновения соответствуют начальному и конечному этапу свободного движения частиц, когда влияние взаимодействия частиц на их движение оказывается несущественным.

Удобно ввести скорость центра масс пары частиц, которая остается постоянной в процессе столкновения,

приведенная масса частиц, участвующих в столкновении. Подстановка соотношений (4.5) в уравнение (4.2) дает

12 (m1 + m2 )G 2 + 12 μ12 g 2 = 12 (m1 + m2 )G 2 + 12 μ12 g′2 .

107

Кинетическая энергия центра масс остается неизменной, а равенство кинетической энергии относительного движения частиц до и после столкновения приводит к условию

т.е. в результате столкновения вектор относительной скорости g поворачивается и переходит в g′, но модули этих векторов g = g

остаются неизменными.

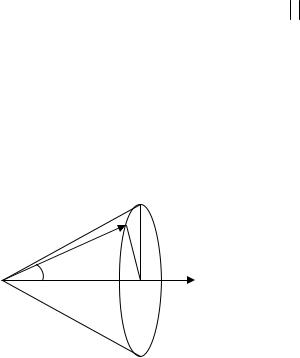
Поворот вектора относительной скорости определяется двумя углами χ и ϕ, вводимыми в сферической системе координат (рис.

4.1). Полярный угол χ называется углом рассеяния. Он является углом между векторами g и g′ в плоскости, образованной этими векторами. Азимутальный угол ϕ определяет положение этой

плоскости относительно некоторой фиксированной плоскости, проходящей через g (в данном случае плоскость чертежа рис. 4.1).

g′ ϕ

χ

g

Рис. 4.1

Связь между векторами g′ и g можно определить тогда соотношением

где i, j, k –взаимно перпендикулярные единичные векторы, причем вектор g направлен вдоль i .

Заметим, что изменение импульса каждой частицы в результате столкновения равно

108

В случае центрально-симметричного потенциала взаимодействия частиц угол ϕ зависит только от взаимного расположения сталки-

вающихся частиц, поэтому при статистическом рассмотрении столкновений для определения средней передачи импульса по азимутальному углу можно произвести усреднение. Поскольку

cos ϕ = sin ϕ = 0 , получаем

Аналогичным образом можно показать, что средняя передача энергии при столкновениях частиц определяется выражением [8,13]

В качестве характерного примера рассмотрим частный случай, когда массы сталкивающихся частиц резко различаются (m1 << m2 ). Это имеет прямое отношение, например, к случаю уп-

ругого столкновения электрона с атомами или ионами. Положение центра масс при этом фактически совпадает с положением тяжелой частицы, относительная скорость практически равна скорости электрона, а приведенная масса – массе электрона. Выражения для

Из этих соотношений следует, что величина относительной потери импульса электрона при его столкновении с тяжелой частицей имеет порядок единицы, а относительное изменение его энергии пропорционально малому отношению масс электрона и атома или иона.

109

4.2.Сечения рассеяния и эффективные сечения столкновений частиц

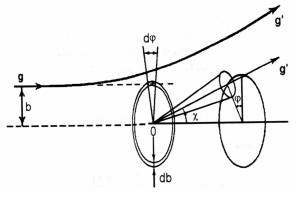
Для дальнейшего обсуждения полезно ввести понятие дифференциального сечения рассеяния. Рассмотрим однородный пучок частиц, налетающих на силовой центр с начальной скоростью g и

имеющих все возможные значения прицельного параметра b (рис. 4.2). Число частиц, рассеянных в единицу времени в элемент телесного угла dΩ = sin χdχdϕ, пропорционально плотности потока

частиц в пучке I0 и величине dΩ . Тогда дифференциальное сечение рассеяния σ(g, Ω) oпределяется таким образом, что величина I0σ dΩ равна числу частиц, рассеиваемых за 1 с в элемент телесного угла dΩ .

Рис. 4.2

Из рис. 4.2 видно, что такое же число частиц проходит через элемент кольца bdbdϕ , поэтому

I0σ(g,Ω)dΩ = I0bdb dϕ ,

откуда следует

110