Березкин Основы теории информации и кодирования 2010

учетом дискретности. Математическое ожидание и дисперсия равны:

J ( X ) 1 12 3 14 4 14 2,25 ;

D[J (xk )] J 2 (xk ) p(xk ) (2,25)2 1,7 .

J

1 2 3 4

Рис. 6.6. Распределение вероятностей

F(J ) p{J (uk ) J}

1

1/2

J

1 2 3 4

Рис. 6.7. Функция распределения вероятностей

6.5. ЭНТРОПИЯ

Собственная информация сообщения J (xk ) log2 p(xk ) ин-

терпретируется как количество информации, требуемое для однозначного определения этого сообщения. Среднее количество информации, необходимое для идентификации любого сообщения из

множества X , носит название энтропии

H ( X ) p(xk ) log2 p(xk ) m[J (xk )] J ( X ) .

xk X

Энтропию можно рассматривать как меру неопределенности сообщения до того, как это сообщение принято.

151

Для полного понимания этой важнейшей для практических приложений меры количества информации рассмотрим основные

еесвойства.

1.H (X ) является непрерывной неотрицательной функцией

факта, что бесконечно малое приращение вероятности в любой

4. Энтропия достигает максимального значения при равенстве p(x1 ) p(x2 ) ... p(xn ) 1n . Доказательство этого свойства

проведем с использованием метода неопределенных множителей Лагранжа. Максимизацию H (X ) можно представить как решение

экстремальной задачи с ограничением:

Поиск условного экстремума заменим на нахождение безусловного экстремума за счет введения неопределенного множителя и функционала

Необходимое условие максимума для произвольного k можно представить в следующем виде:

152

множества сообщений достигает наибольшего значения, когда все сообщения равновероятны. Другими словами, среднее значение информации, необходимое для однозначного определения сообщения из множества возможных сообщений, достигает своего максимума, когда все сообщения равновозможны.

5. Энтропия H (X ) удовлетворяет неравенству H ( X ) log2 n ,

а знак равенства достигается при p(xk ) p 1n , k 1, n . Это ут-

верждение можно доказать, воспользовавшись неравенством ln a a 1 , которое следует из того факта, что функция ln a касается прямой a 1 в точке a 1 и ее наклон является монотонно убывающей функцией (рис. 6.8). Преобразования

подтверждают утверждение H ( X ) log2 n . Знак равенства имеет

место, когда a np(1xk ) 1.

Для двумерного случая, когда n 2 , энтропию можно предста-

вить в виде H (X ) p log2 p (1 p) log2 (1 p) , где p – вероятность появления одного из двух сообщений (рис. 6.9).

Основной смысл формулы H ( X ) log2 n может быть еще

сформулирован в следующем виде. Для любого заданного алфавита X количество информации, которое в среднем может содер-

153

жаться в одном символе xk X , достигает максимума, когда все

символы используются равновероятно. Это максимально возможное среднее значение информации на символ называют информа-

ционной пропускной способностью алфавита. Она равна log2 X . Например, пропускная способность русского алфавита

равна log2 33 5 бит/симв.

ln a

-1

Рис. 6.8. Графическая иллюстрация неравенства ln a a 1

H ( X )

1

Рис. 6.9. Энтропия для случая n 2

Энтропия максимальна, если буквы алфавита равновероятны и взаимно независимы. Если появление букв не равновероятно, то ээнтропия уменьшается. Еще меньшей будет энтропия при наличии статистической связи букв. Мерой количественной оценки избы-

точности алфавита является коэффициент избыточности

КИ Hmax ( X ) H ( X ) .

Hmax ( X )

Имеется определенная избыточность и в русском языке. Статистика появления букв алфавита в тексте приведена в табл. 6.4, а в

154

табл. 6.5 – оценка статистической связи букв [1]. Следовательно,

Таблица 6.5

Изучение последующих свойств энтропии требует введения понятий взаимной и условной энтропии для XY .

Взаимная энтропия интерпретируется как среднее количество

( xk , yi ) XY

Аналогично выводятся формулы:

H ( X ;Y ) H ( X ) H ( X / Y ) H (Y ) H (Y / X );

H ( XY ) H ( X ) H (Y / X ) H (Y ) H ( X / Y ).

155

Условная энтропия вычисляется в соответствии со следующим выражением, что следует из определения энтропии:

Отметим, если в системе нет потерь и искажений, то условные энтропии равны нулю.

6. Для заданного произведения множеств XY условная энтропия удовлетворяет неравенству H (Y / X ) H (Y ) , в котором знак

равенства имеет место только тогда, когда события xk и yi статистически независимы, т.е. p( yi ) p( yi / xk ) . Данное неравенство

показывает, что статистическая зависимость, например, символов алфавита не может увеличить количество информации на символ. Доказательство проведем уже известным способом:

7. Введем в рассмотрение условное среднее значение взаимной

8. Для заданного произведения множеств XY условное среднее значение взаимной информации величина неотрицательная, т.е.

J (X ; yi ) 0 , здесь знак равенства достигается при p(xk ) p(xk / yi ) . Данное свойство оказывается важным в том случае, когда yi – символ, принятый на выходе канала с шумом, а xk – какое-либо из сообщений. Неравенство устанавливает, что

средняя информация, содержащаяся в принятом символе относительно переданного сообщения, всегда неотрицательна (рис. 6.10,а).

156

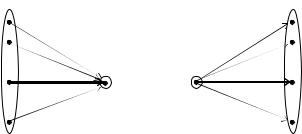
9. По аналогии J (xk ;Y ) 0 . Это означает, что если xk – сообщение, передаваемое по каналу с шумом, то средняя информация о сообщении xk , полученная по этому каналу (рис. 6.10,б), неотрицательна.

Рис. 6.10. Иллюстрация условного среднего значения взаимной информации:

а – J ( X ; yi ) ; б – J (xk ;Y )

10. Взаимная энтропия всегда неотрицательна, т.е.

H ( X ;Y ) 0 .

Доказательство свойств 8, 9 и 10 проводится аналогично доказательству свойств 5 и 6.

Подведем некоторые итоги. Рассмотрим два различных выражения для взаимной энтропии:

H (X ;Y ) H ( X ) H ( X / Y );

H (X ;Y ) H (Y ) H (Y / X ).

Эти два выражения особо интересны, когда xk является сообщением, передаваемым по каналу с шумом, а yi – соответствую-

щим принятым символом.

При интерпретации первого соотношения мы понимаем:

– энтропию H (X ) как среднее количество переданной инфор-

мации (энтропия источника);

– взаимную энтропию H ( X ;Y ) как среднее количество ин-

формации, полученной о переданном сообщении;

– условную энтропию H ( X / Y ) как среднее количество информации, которое все еще потребуется для определения xk после

157

приема символа yi , т.е. потерянное вследствие шума, или короче,

ненадежность передачи.

Второе соотношение подчеркивает другой взгляд на среднее количество информации, а именно, как на разность между средним количеством информации, необходимым для определения принятого символа, и средним количеством информации, необходимым для определения того же сигнала, когда известно переданное со-

общение. Следовательно, H (Y / X ) есть среднее количество ин-

формации, необходимое для определения помехи, имеющей место в канале, и мы можем понимать эту величину как энтропию шума в

канале. Другими словами, H (Y / X ) является частью энтропии Y , которая возникает вследствие шума в канале.

ЗАДАЧИ

6.1.Урна содержит 5 черных и 10 белых шаров. Случайно, без возвращения, из урны выбирают три шара, и результат выбора передают по линии связи. Пусть выбрано: черный – черный – белый. Какое количество информации передается, если хотят сообщить:

а) о порядке шаров, их цвете, количестве белых и черных; б) только о количестве черных и белых шаров?

6.2.На борту самолета имеется дублированная вычислительная система, состоящая из двух одинаковых ЭВМ. Надежность одной

ЭВМ p 0,96 . Сколько надо передать информации по радиокана-

лу, чтобы сообщить об отказе вычислительной системы?

6.3. Система описывается дискретным стационарным марковским процессом с матрицей переходов

Сколько информации содержится в сообщении о том, что система находится в состоянии с номером "1"?

158

6.4. Система описывается дискретным стационарным марковским процессом, граф переходов которой имеет вид

Сколько информации содержится в сообщении о том, что система находится в состоянии с номером "2"?

6.5.Сколько информации содержится в сообщении о том, что сумма очков на двух брошенных игральных костях равна 7?

6.6.На двухэлементном множестве X (x1 , x2 ) задано распре-

Определить:

а) энтропии ансамблей X , Y и XY ;

б) условные энтропии H ( X / Y ) и H (Y / X ) ; в) взаимную энтропию H (X ;Y ) ;

г) условные средние значения взаимной информации J ( X ; yi )

и J (xk ;Y ) ;

д) частную условную энтропию H (Y / xk ) .

6.8. Пусть x1 , x2 – буквы алфавита на входе канала, а y1 , y2 , y3 –

буквы выходного алфавита. Символы на входе канала появляются равновероятно, а последовательность букв во входной и выходной

159

последовательностях статистически независима. Условные вероятности имеют вид

Построить функцию распределения для взаимной информации

I (xk ; yi ) . Определить взаимную энтропию H ( X ;Y ) .

6.9. Группа из четырех сообщений кодируется двоичным кодом

Найти энтропию множества сообщений и среднюю длину кодовых слов. Показать, что если сообщения статистически независимы, то при передаче последовательности кодовых слов символы “0” и “1” появляются равновероятно.

6.10.Среди группы ПВО ¼ составляют зенитные орудия (x1),

½– ракетные установки (x2), ¼ – самолеты-перехватчики (x3). Пусть ракетные установки с вероятностью ½ поражают цель, са- молеты-перехватчики всегда поражают цель, а зенитные орудия всегда не попадают.

Какое количество информации содержится в сообщении y: «средство ПВО поразило цель относительно факта использования

xk »?

Какое количество информации содержится в сообщении z: «средство ПВО три раза подряд поразило цель относительно факта использования x2 »?

6.11. От источника информации поступают статистически независимые символы с вероятностями 1/4 и 3/4. Найти энтропию последовательности из 100 двоичных символов.

160