3.2 Условие кинетостатической определимости кинематических цепей
Для каждого звена плоского механизма можно написать три уравнения равновесия; для n звеньев число уравнений равновесия будет 3n.
Реакция каждой одноподвижной пары содержит две неизвестных:
вращательная пара (рис.27):
модуль реакции Fij;
угол αij;
поступательная пара (рис.28):
модуль реакции Fij;
координату приложения реакции хij;
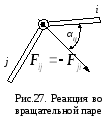
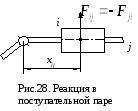
Реакция двухподвижной (высшей) пары (рис.28) содержит одну неизвестную – модуль реакции Fij, так как направление этой реакции (нормаль n-n к соприкасающимся поверхностям) и точка приложения реакции известны.
Условие кинетостатической определимости механизма заключается в равенстве числа уравнений равновесия числу неизвестных реакций связи:
Если
механизм содержит только низшие
(одноподвижные) пары, то это условие
принимает следующий вид:
,
или
(3.3)
Если в механизме
есть избыточные связи, то есть
,
то необходимо к уравнениям кинетостатики
добавить уравнения деформаций.
3.3 Планы сил
Метод планов сил служит для графического определения реакций в плоских механизмах. В отличие от аналитических методов, графический метод прост и нагляден. Однако графический метод менее точен, чем аналитический.
Построение планов сил рассмотрим на примере рычажного четырехзвенника.
Механизм условно расчленяется на структурные группы (рис.29).
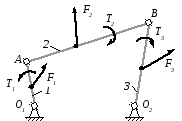
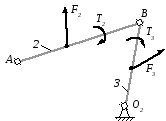
Рис.29. Декомпозиция механизма
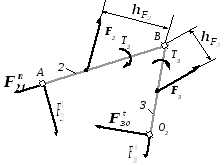
Решение задачи начнем с рассмотрения условий равновесия наиболее удаленной от ведущего звена группы, образованной звеньями 2 и 3 (рис.30,а).
Каждую из реакций F21 и F30 раскладываем на две взаимно перпендикулярные составляющие:
нормальные
и
;
тангенциальные
и
.
Направление (знак) этих составляющих выбираем произвольно. Если после решения какая-либо составляющая получилась со знаком "-", значит, направление этой силы следует поменять на противоположное.
Определяем
тангенциальные составляющие
и
.
Для этого составляем уравнение моментов
сил относительно точкиВ:
для звена 2:
;
для звена 3:
,
откуда
;
.
Определяем
нормальные составляющие
и
.
Для этого используем графическое решение
векторного уравнения равновесия суммы
сил, действующих на всю группу в целом:
Выбрав масштабный
коэффициент μF,
откладываем на плане сил (рис.30,б)
векторы, отображающие силы
.
Что касается
векторов
и
,
то мы можем указать на плане линии
действия этих сил:
||AB,
||BO2.
Точка пересечения этих линий определит
величину и направление этих векторов.
Суммы нормальных и тангенциальных
составляющих дают полные реакции
и
.
а)
б)
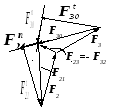
Рис.30. Схема нагружения и план сил для
группы, образованной звеньями 2 и3
Определяем реакцию F23=- F32. Для этого составляем векторное уравнение суммы сил, действующих на одно из звеньев группы, например, звено 2:
Из этого уравнения следует, что искомый вектор F23 на плане сил (рис.30) будет соединять конец вектора F2 с началом вектора F21.
Затем выполняем силовой анализ следующей структурной группы – начального двузвенника, включающего звено 1(рис.31,а).
Для звена 1 можно составить два уравнения равновесия:
векторное уравнение суммы сил
;
скалярное уравнение суммы моментов
В соответствии с первым уравнением строим план сил (рис.31,б), из которого находим силу F10.
Второе уравнение должно обращаться в тождество при заданном значении момента Т1. В ряде случаев этот момент подлежит определению как уравновешивающий, обеспечивающий движение механизма по данному закону.
б)
а)
F12
О1
hF1
hF12
F1
А
T1
Рис.31. Схема нагружения и план сил для
начального двузвенника
1