1.18.Пространственная система сходящихся сил.

Условие равновесия пространственной системы сходящихся сил определяется тремя уравнениями:

; ;. (18.1)

Пример №9. Определить усилия в шести стержнях, соединенных своими концами шарнирно друг с другом и с неподвижными опорами. В узлах К и М приложены силы и, составляющие с положительным направлением координатных осей углы, равные соответственно,,для силыи,,для силы. Взаимное расположение стержней в конструкции определяется угламии(рис.45).

Р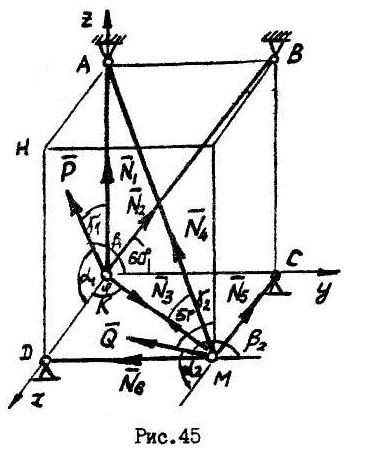ешение:

Так как для системы сходящихся сил можно составить три уравнения равновесия, расчет начинаем с узла К, в котором сходятся стержни 1,2,3. Предполагаем все стержни растянутыми. Растягивающие усилия в стержнях ,инаправлены от узлаК. Составим три уравнения равновесия:

(1)

(2)

(3)

из (1):

из (2):

из (3):

Рассмотрим равновесие узла . Усилияиравны по модулю и противоположны по направлению. Усилиесоставляет с плоскостьюугол. Для нахождения проекции усилияна координатные оси, необходимо предварительно найти проекцию на плоскость, а затем составляющие этой проекции на каждой из координатных осей. Составим три уравнения равновесия для системы сходящихся сил, приложенных к узлу:

(4)

(5)

(6)

из (6):

из (4):

из (5):

Знаки показывают, что стержни 1,3,4 – сжаты, а 2,5,6 – растянуты.

1.19. Равновесие произвольной пространственной системы сил.

Для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно соблюдения следующих условий:

; ;

; ;. (19.1)

Следовательно, число неизвестных не должно превышать числа возможных уравнений равновесия. В некоторых случаях число возможных уравнений равновесия может быть уменьшено. Так, если все силы, приложенные к твердому телу, лежат в плоскости , то уравнения проекций этих сил на осьобращаются в тождество, и число уравнений равновесия сокращается до пяти.

Пример №10.

Однородная прямоугольная плита весом со сторонамиизакреплена в точкесферическим шарниром, в точкецилиндрическим шарниром и удерживается в равновесии невесомым стержнем(рис.46). На плиту действует пара сил с моментоми силыи. Силалежит в плоскостии составляет с осьюугол, силалежит в плоскостии составляет с осьюугол.

Определить реакции связей при ,,.

Решение:

На плиту действуют активные силы ,,, пара сил с моментом, а также реакции связей. Реакцию сферического шарнираразложим на три составляющие,,, цилиндрического шарнира(подшипника) – на две составляющиеи, реакциюневесомого стержня направим вдоль стержня, предполагая, что он растянут. Для определения шести неизвестных реакций связей составим шесть уравнений равновесия действующих на плиту сил:

(1)

(2)

(3)

(4)

(5) (6)

Для определения момента силы относительно координатных осей, раскладываем силуна две составляющиеи, численно равные проекциям этой силы на осиZ и X соответственно: ,.

Решая систему уравнений (1)-(6), находим искомые величины:

из (5):

из (6):

из (1):

из (2):

из (4):

из (3):

Для проверки можно составить уравнение моментов относительно оси , проведенной через точку:

Реакции связей, значения которых получены отрицательными, имеют направления, противоположное показанному на чертеже.

Пример №11.

На косозубое колесо вала редуктора диаметром действует осевая сила, радиальнаяи неизвестное окружное усилие. На прямозубое колесо диаметром, закрепленное на том же валу, действует радиальная сила(рис. 47).

Определить реакции подшипников при следующих размерах: ;;.

Решение:

Опорой горизонтального вала в точке является радиальный подшипник, его реакцию раскладываем на две составляющиеи. В точке- радиально-упорный подшипник. Его реакцию раскладываем на три составляющие,,. Шестой неизвестной величиной является окружное усилие. Составим для вала шесть уравнений равновесия:

(1)

(2)

(3)

(4)

(5)

(6)

Решая систему уравнений (1)-(6), находим неизвестные величины:

из (2):

из (5):

из (6):

из (1):

из (4):

из (3):