2.9. Сложное движение точки.

В ряде случаев движение точки можно рассматривать по отношению к двум системам отсчета, из которых одну можно считать условно неподвижной. Например, движение человека по движущейся лодке (рис. 107) по отношению к берегу является сложным, состоящим из движения относительно лодки (подвижная система отсчета) и движение вместе с лодкой по отношению к берегу (неподвижная система отсчета).

Движение точки относительно неподвижной системы отсчета называется абсолютным движением. Движение точки относительно подвижной системы отсчета называется относительным. Движение точки вместе с подвижной системой отсчета относительно неподвижной системы отсчета является для точки переносным.

П

ри сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей.

, (2.40)

где - абсолютная скорость точки в движении относительно неподвижной системы отсчета;

- относительная скорость точки, скорость движения относительно подвижной системы отсчета;

- переносная скорость точки, скорость той точки подвижной системы отсчета, с которой в данный момент времени совпадает движущаяся точка.

Если переносным движением является вращательное движение (рис. 108), переносной скоростью для точки будет являться скорость точки вращающегося конуса (подвижной системы отсчета), где в данный момент времени находится движущаяся точка М.

Численное значение скорости зависит от угловой скорости вращающегося тела и расстоянияточки до оси вращения. Расстояниезависит от относительного движения точки вдоль образующей конуса. Модуль абсолютной скорости определяется по правилу параллелограмм:, (2.41)

где - угол между направляющими векторови. Если векторыивзаимно перпендикулярны (рис. 108), то

. (2.42)

Если векторы илежат в одной плоскости (рис. 109), то модуль абсолютной скорости удобно определить по проекциям на координатные оси

,

где ,.

Абсолютное ускорение точки равно геометрической сумме трех ускорений:

• относительного 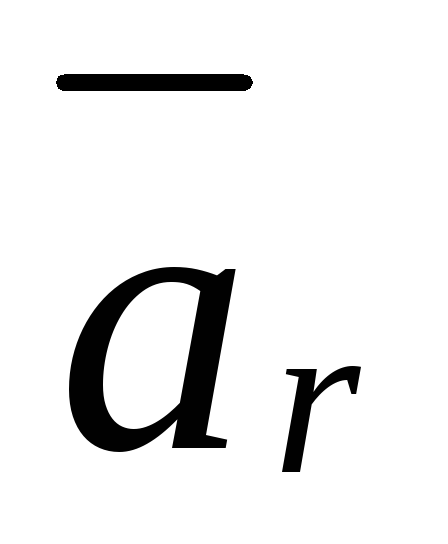, характеризующего изменение относительной скорости точки в относительном движении;

• переносного , характеризующего изменение переносной скорости точки в переносном движении;

• ускорения Кориолиса 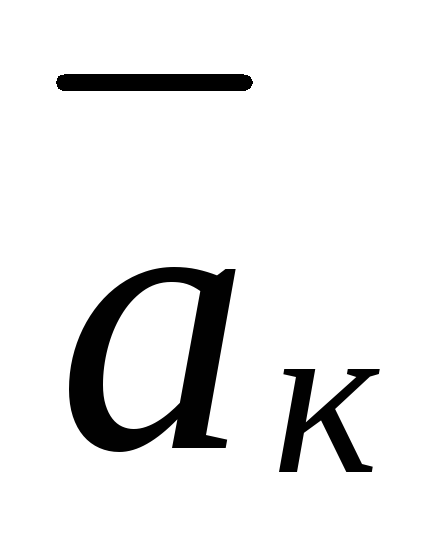, характеризующего изменение относительной скорости точки в переносном движении и переносной скорости точки в относительном движении:

. (2.43)

Относительное и переносное ускорение определяется из закона соответствующего движения. Ускорение Кориолиса вычисляется по формуле:

, (2.44)

где - угловая скорость переносного вращательного движения.

Модуль ускорения Кориолиса зависит от угла между векторами и:

. (2.45)

Ускорение Кориолиса равно нулю, если а) , т.е. переносное движение не является вращательным; б) векторыипараллельны между собой, т.е.

.

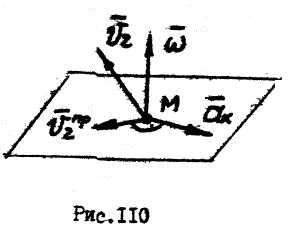
Чтобы определить направление вектора ускорения Кориолиса по правилу Жуковского необходимо:

1. перенести в точку М вектор угловой скорости переносного вращательного движения;

2. спроецировать вектор относительной скорости на плоскость, перпендикулярную вектору;

3. повернуть проекцию нав сторону вращения (рис. 110).

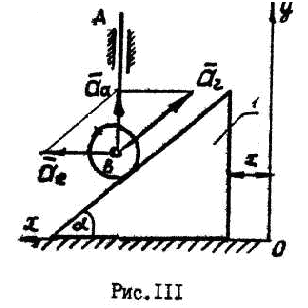
Если переносное движение поступательное, то ,, поэтому абсолютное ускорение будет равно геометрической сумме относительного и переносного ускорений (рис. 111):

. (2.46)

При решении задач на сложное движение точки рекомендуется придерживаться следующего порядка:

1. Выяснить, какое движение точки является абсолютным, какое относительным и какое переносным.

2. Используя закон относительного движения, определить положение точки в заданный момент времени.

3. Вычислить относительную и переносную скорости точки, показать векторы переносной и относительной скорости. Вычислить абсолютную скорость точки по правилу параллелограмма или по проекциям на координатные оси.

4. Вычислить составляющие относительного и переносного ускорения и показать на схеме их векторы.

5. В случае переносного вращательного движения определить модуль и направление ускорения Кориолиса.

6. Вычислить модуль абсолютного ускорения точки по проекциям на координатные оси.

ПРИМЕНЕНИЕ ТЕОРЕМЫ О СЛОЖЕНИИ СКОРОСТЕЙ.

Пример №20.

Электромотор (рис. 112), установленный на горизонтальном фундаменте без креплений, движется поступательно и прямолинейно по закону:

.

Ротор мотора вращается вокруг оси согласно уравнению. Определить абсолютную скорость точки ротора, отстоящей от оси вращения ротора на расстояниив момент времени. Положение точки М определяется углом.

Р

ешение:

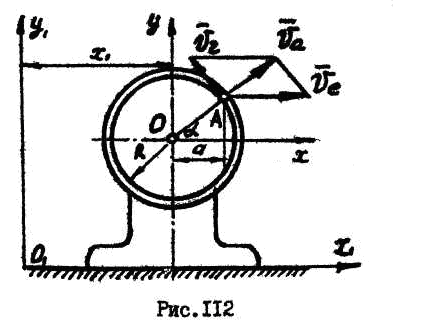
1. Точка совершает абсолютное движение относительно неподвижной системы отсчета. Подвижная система отсчетажестко связана с электромотором. Абсолютное движение точки состоит из относительного движения по окружности радиусаR со скоростью и переносного прямолинейного движения вдоль горизонтального фундамента со скоростью.

2. Положение точки в заданный момент времени определено углом .

3. Относительную и переносную скорость точки найдем, используя заданные законы относительного и переносного движения. В относительном движении скорость точки М зависит от угловой скорости вращения ротора и расстояния точки до оси вращения: ,

где ;

.

Следовательно, в заданный момент времени:

.

Переносную скорость точки найдем, дифференцируя по времени уравнение движения электромотора:

;

при t₁=1c .

Абсолютную скорость точки М можно найти по правилу параллелограмма:

.

Учитывая, что .

Абсолютную скорость точки можно найти по проекциям на координатные оси.

; ;.

Пример №21.

Стержень кулисного механизма (рис. 113) движется со скоростью. Для заданного положения механизма определить угловую скорость кулисы, если расстояние.

Решение:

Точка участвует в относительном движении вдоль кулисысо скоростьюи в переносном движении со стержнемсо скоростью. В абсолютном движении точкадвижется по окружности радиусасо скоростью. Зная переносную скорость, можно найти абсолютную скорость движения точки:

.

Учитывая, что , где- угловая скорость кривошипа,.

ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЯЫ ДЛЯ СЛУЧАЯ ПЕРЕНОСНОГО ПОСТУПАТЕЛЬНОГО УСКОРЕНИЯ.

Пример №22.

Колеса тепловоза одинакового радиуса катятся без скольжения по прямолинейному участку пути. Спарник соединяющий кривошипы и ,движется поступательно. Определить абсолютную скорость и абсолютное ускорение точки спарника тот момент, когда угол поворота кривошипов и ,равен и (рис.114), а тепловоз движется с постоянной скоростью .

Решение:

1. Спарник ,на котором находится точка ,дви­жется поступатель­но, следовательно, все точки спарника движутся по одина­ковым траекториям - окружностям ради­уса иимеют равные скорости и ускорения.

где - угловая скорость колеса.

Угловую скорость колеса определим, принимая во внимание, что колесо совершает плоскопараллельное движение, центр колеса движется со скоростью , а мгновенный центр скоростей колеса находится в точке:

.

Тогда

.

Абсолютную скорость точки найдем по проекциям на координатные оси:

;

;

где ;

;

.

2. Так как переносное движение является поступательным, абсолютное ускорение точки определим по формуле:

, (2)

где ,.

ПРИМЕНЕНИЕ ТЕОРЕМЫ КОРИОЛИСА.

Пример №23.

Диск радиуса , закрепленный шарнирно в точке(рис.115), вращается вокруг неподвижной оси с угловой скоростью. По ободу диска движется точкасогласно закону относительного движения, (- в сантиметрах,- в секундах). Найти абсолютную скорость и абсолютное ускорение точкив момент времени.

Решение:

1. Сложное движение точкискладывается из относительного движения по ободу диска по законуи переносного вращательного движения с диском относительно оси.

2. Положение точки в заданный момент времени определяется дуговой координатой :.

.

Дуге соответствует центральный угол:

.

По условию задачи задано положительное направление отсчета относительной координаты . Так как дуговая координатаи соответствующий ей угол получены с отрицательными знаками, откладываем уголв отрицательном направлении.

3. Выразим абсолютную скорость точки:

, (1)

где ,

.

Так как -равносторонний,.

В заданный момент времени:

,

.

Вектор относительной скорости направлен в соответствии с полученным знаком. Значение абсолютной скорости точкиопределим по проекциям на координатные оси:

;

;

.

4. Абсолютное ускорение точки определим по теореме Кориолиса:

. (2)

Так как в переносном и относительном движении точка движется неравномерно по криволинейным траекториям, уравнение (2) примет вид:

(3)

Вычислим слагаемые абсолютного ускорения:

,

.

Совпадение знаков относительной скорости и касательной составляющей относительного ускорения показывает, что относительное движение точки является ускоренным.

,

.

Так как диск вращается с постоянной угловой скоростью, то .

Ускорение Кориолиса:

.

Модуль абсолютного ускорения определим, проецируя векторное равенство (3) на координатные оси:

;

;

.

Пример №24.

Рабочее колесо компрессора с прямолинейными каналами (рис.116) равномерно вращается с угловой скоростью вокруг оси, перпендикулярной плоскости чертежа. Воздух течет по каналам с постоянной относительной скоростью. Найти абсолютную скорость и абсолютное ускорение для частицы воздуха, находящейся в точкеканала, наклоненного под углом, если.

Р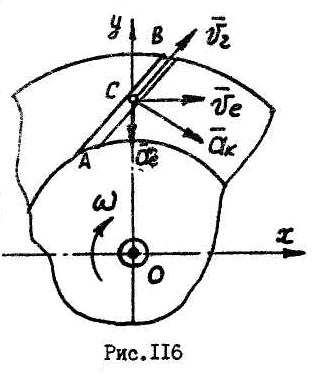ешение:

1. Определим абсолютную скорость точки по теореме о сложении скоростей:

, (1)

где - относительная скорость движения частицы воздуха по каналу;

- переносная скорость, т.е. скорость точкиканала, в которой в данный момент времени находится частица воздуха.

.

Модуль абсолютной скорости определим, проецируя векторное равенство (1) на координатные оси:

,

,

.

2. Определим абсолютное ускорение точки по теореме Кориолиса:

(2)

Относительное ускорение , так как по условию задачи частица воздуха движется по каналус постоянной скоростью:

.

Ускорение Кориолиса:

.

Спроецируем векторное равенство (2) на координатные оси:

,

,

.

Пример №25.

Кулисный механизм состоит из двух параллельных валов и, кривошипаи кулисы(рис.117). Кривошипвращается равномерно вокруг осис постоянной угловой скоростью. Каменьперемещается вдоль прорези кулисы. Найти угловую скорость и угловое ускорение кулисы в момент времени, когда угол поворота кривошипа, если расстояние между осями валов.

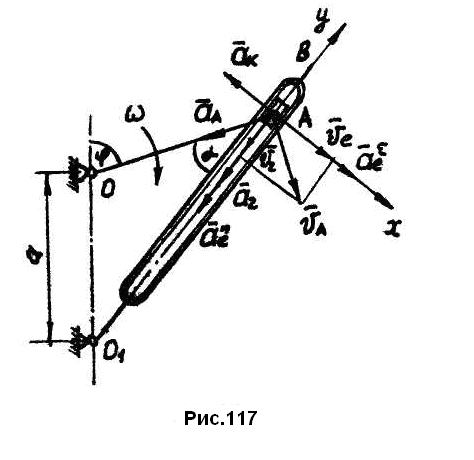
Решение:

1. Абсолютным движение точки является вращение вместе с кривошипомвокруг осис угловой скоростью:

.

Вектор абсолютной скорости можно разложить на две составляющие: вектор относительной скорости точкивдоль прорези кулисы и векторпереносной скорости вращения кулисывокруг оси, тогда:

,.

Так как равнобедренный,, т.е.

,

.

Так как переносным движением для точки является вращение кулисы вокруг оси, а величина переносной скоростиопределена, можно найти угловую скорость кулисы:

.

2. Определим абсолютное ускорение точки:

.

Выразим абсолютное ускорение точки по теореме Кориолиса:

, (1)

где ,

; (2)

- угловое ускорение кулисы.

Вычислим ускорение Кориолиса:

.

Для нахождения углового ускорения кулисы спроецируем векторное равенство (1) на ось:

;

.

Учитывая соотношение (2), найдем угловой ускорение кулисы:

.

т.е кулиса вращается с постоянной угловой скоростью.

Пример №26.

По радиусу диска (рис.118), вращающегося вокруг вертикальной оси с угловой скоростьюв направлении от центра диска к ободу по закону, движется точка. Радиуссоставляет с осью вращения угол. Определить величину абсолютного ускорения точки в момент.

Решение:

1. Абсолютное ускорение точки можно определить по теореме Кориолиса:

(1)

Зная закон относительного движения, можно найти относительное ускорение точки:

;

.

В переносном движении точка движется по окружности радиуса, поэтому:

;

;

.

Ускорение Кориолиса:

.

Направление вектора ускорения Кориолиса определим по правилу Жуковского: перенесем в точку векторугловой скорости переносного вращательного движения, спроецируем векторна горизонтальную плоскость, перпендикулярную вектору, и повернем проекцию нав сторону вращения, т.е. векторнаправлен в сторону, противоположную положительному направлению оси.

Для заданного момента времени :

;

;

.

Вычислим абсолютное ускорение точки по проекциям на координатные оси:

;

;

;

;

.