Ур-е Лагранжа II-го рода.

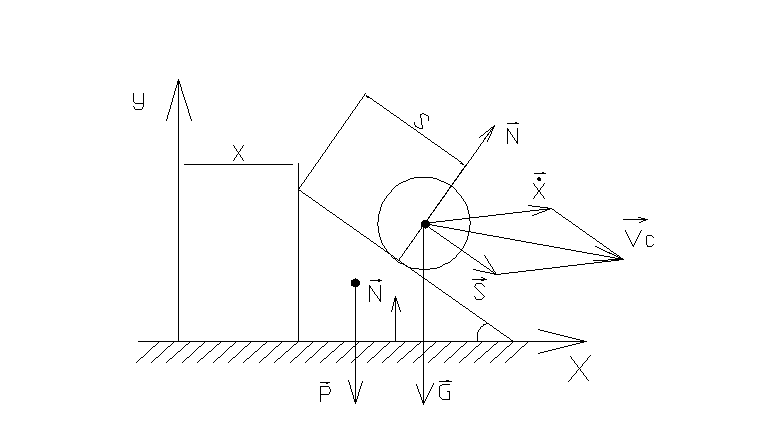
Рассм. мех. систему с одной степенью свободы с идеальными связями. ЕЕ движение в полной мере описывает одно ур-е Лагранжа II-го рода.

Производная по времени от частной производной кинетической энергии по обобщенной скорости «-» частная произв. кинетич. Энергии по обобщенной координате = обобщ. силе.

;

Опред. кинетическую эн. сист-мы.

; ;

;

; ;

Вынужденные колебания с учётом сил сопротивления

…Q^П – часть обобщённой силы, зависит от действия

Q^Ф – часть обобщённой силы, зависит от сил сопротивления

Q^B – часть обобщённой силы, зависит от действия возмущающей силы

, pt – часть возмущающей силы

Произведём все действия, предусмотренные уравнение Лагранжа

где

q=q₁+q₂

q₁ зависит от вида корней характеристического уравнения.

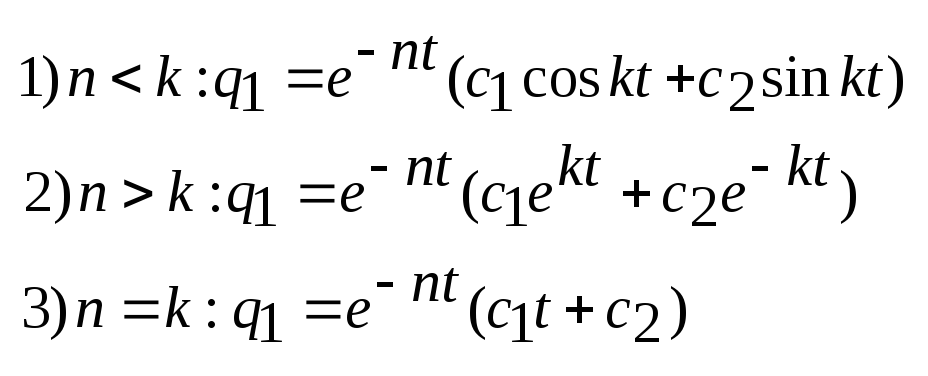
В каждом из приведенных решений есть множитель. Это говорит о том, что колебания, описываемые этой формулой быстро затухают.

Частное решение q₂ ищем в виде:

где А₂ – амплитуда вынужденных колебаний

p – частота

δ – начальная фаза

ε – сдвиг по фазе

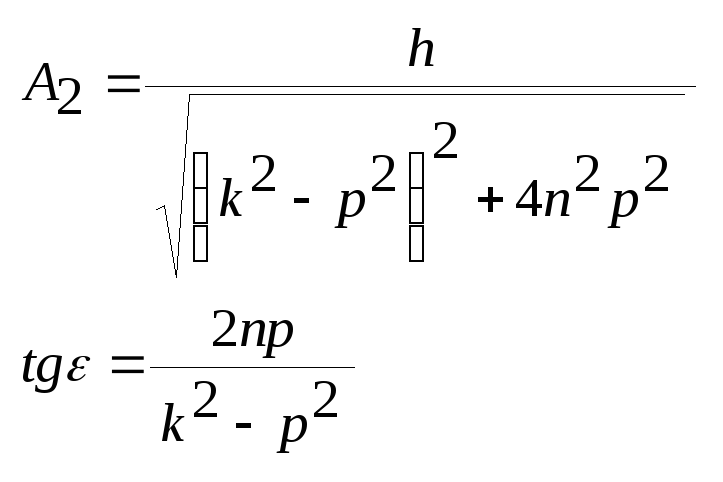
0≤ε≤π

Свойства вынужденных колебаний:

1. не затухают

2. амплитуда – величина постоянная

3. частота совпадает с частотой вынуждающей силы

4. характеристики колебаний не зависят от начальных условий

Малые колебание механической с-мы с учётом сил сопротивления.

Они описываются ур-ием

где - часть обобщённой силы, зависящей от потенциальной силы.

- часть обобщённой силы, зависящей от действия сил сопротивления.

Линейные силы сопротивления , т.е. пропорциональны скорости, где μ – коэффициент, характеризующий св-ва вязкой среды, либо соприкасающихся трущихся поверхностей. По определению обобщённой силы запишем. Используя тождество Лагранжа и меняя порядок суммирования, получаем:

-ф-ция Релея, характеризует скорость убывания полной энергии с-мы в зависимости от сил сопротивления. .

Возьмём функцию Релея в виде: .

Произведём все операции дифференцирования и подстановки в ур-ие Лагранжа:

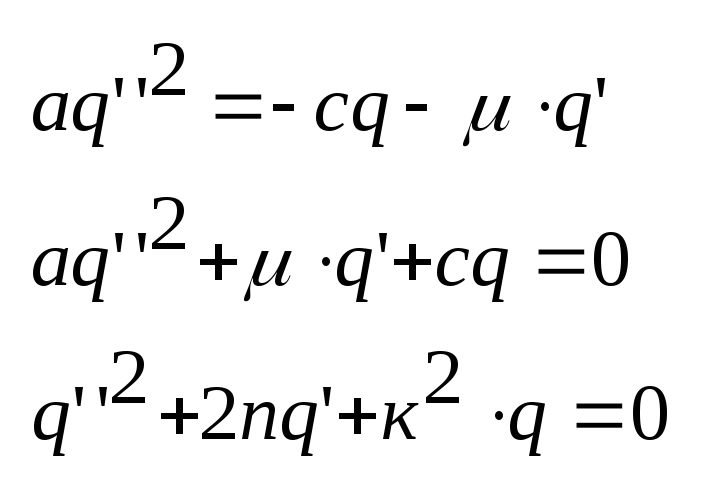
где,n – обобщённый коэффициент сопротивления системы.

-циклическая частота.

Получаем ДУ 2-го порядка без правой части, решение которой зависит от вида корней характеристического уравнения, характеризует колебания движения системы с учётом сил сопротивления.

Составим такое уравнение

Возможны 3 случая:

1) n<k

Если корни такие (мнимые), то решение ищем в виде:

При

- ур-ие затухающих колебаний.

В амплитудной форме:

α – начальная фаза колебаний

А – условная амплитуда колебаний

-фаза.

Важной характеристикой затухающих колебаний является отношение 2-х последовательных максимумов – декремент затухания-логарифмический декремент затухания – величина обратная числу колебаний, за которое время амплитуда уменьшается в е раз.

-знаменатель геометрической прогрессии.

2) n>k

. Оба корня действительные и отрицательные.

Решение ищем в виде. Для определенияc1 и c2 дифференцируем ур-ие и при t=0 определяем. Движение носит апериодический характер.

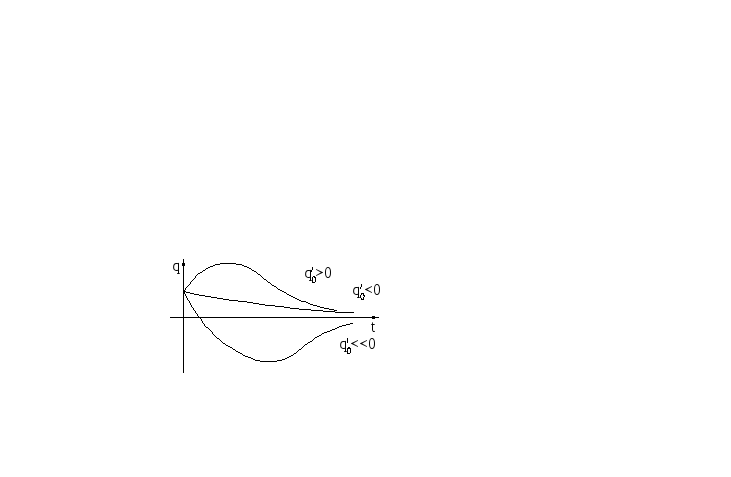
3) n=k – случай критического сопротивления. Ур-ие получаем в виде.c1 и c2 определяются дифференцированием. Движение носит апериодический характер.

Вынужденные колебания механической системы без учета сил сопротивления.

Возможны 2 случая:

и

1)

- решение будем искать в виде правой части

- уравнение вынужденных колебаний без учета сил сопротивления.

,

2)

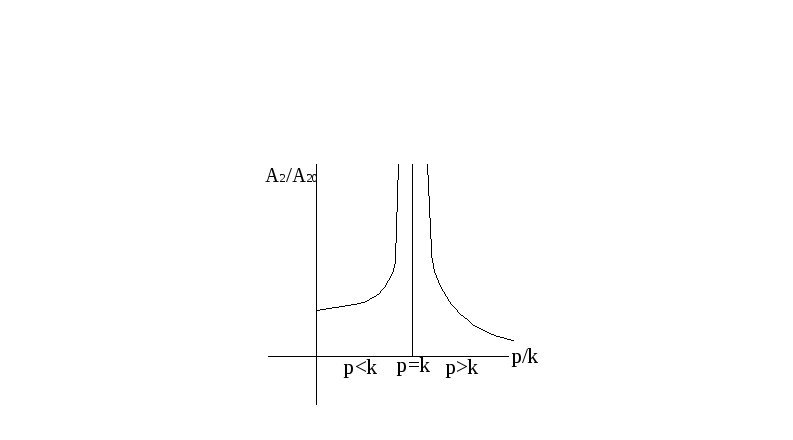
- Амплитуда.

Малые свободные колебания механической системы. (собственные)

Колебательное движение – движение, при котором одна или несколько обобщенных координат периодически принимают нулевые значения. Причиной малых свободных колебаний служат: начальное отклонение или придание объекту начальной скорости.

Устойчивость. Положение механической системы может быть равновесным или нет. В свою очередь положение равновесия может быть устойчивым, неустойчивым и безразличным.

Устойчивое положение – когда при малом изменении обобщенной координаты тело стремится занять исходное положение.

1– устойчивое положение;

2 – неустойчивое;

3 – безразличное.

Устойчивость положения определяется теоремой Лагранжа-Де-Рихле, которая носит достаточный характер.

В положении равновесия все обобщенные координаты имеют нулевое положение и их отсчет ведут от этого положения.

Теорема: для того, чтобы механическая система с голономными идеальными связями находилась в равновесии, достаточно чтобы первая четная производная потенциальной энергии по обобщенной координате была > 0.

- устойчивое положение системы.

Собственные колебания.

Малые свободные колебания всегда линейны. Малые – когда величины малы q, q’,q”, при этом в уравнении Лагранжа эти величины 2-го порядка и выше отбрасываются и колебания всегда описываются линейными уравнениями.

Рассмотрим колебания механической системы с идеальными связями, имеющей одну степень свободы и описанной одним уравнением Лагранжа:

В общем случае структура обобщенной силы складывается из части, зависящей от действия потенциальных сил, сил сопротивления и возмущенных сил.

Рассмотрим механическую систему с консервативными силами:

Для решения уравнения Лагранжа нужно определить кинетическую энергию системы в виде:

а – коэффициент инерции системы, зависит от размерности обобщенной координаты.

Потенциальную энергию ищут в виде: с – коэффициент жесткости системы.

Произведем действия в соответствии с уравнением Лагранжа:

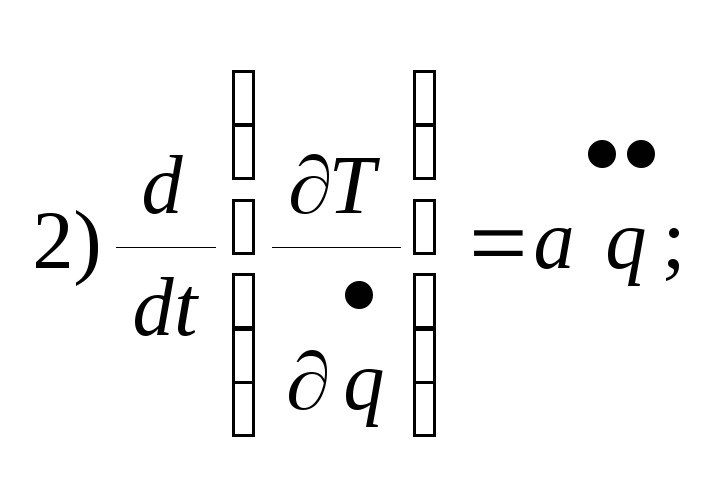
Подставим полученные выражения в уравнение Лагранжа:

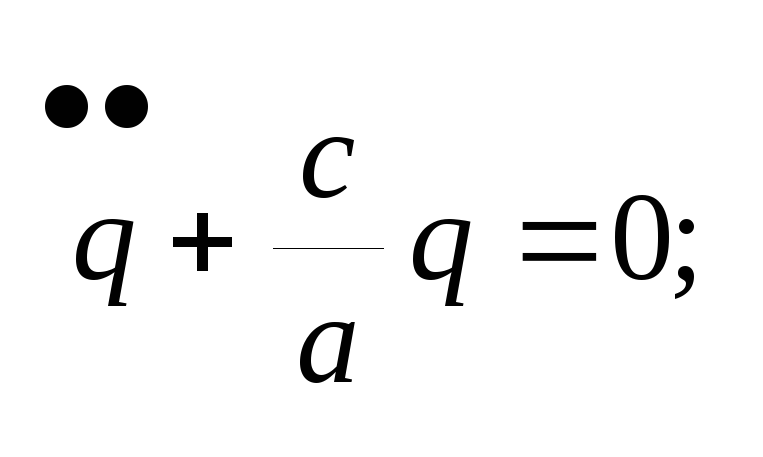
k – циклическая частота колебаний.

В результате уравнение Лагранжа приводиться к дифференциальному уравнению 2-го порядка, однородному без правой части, линейному.

Решение дифференциального уравнения приводится к уравнению, зависящего от корней характеристического уравнения:

то решается в виде:

- решение диф. уравнения.

- обобщенная скорость.

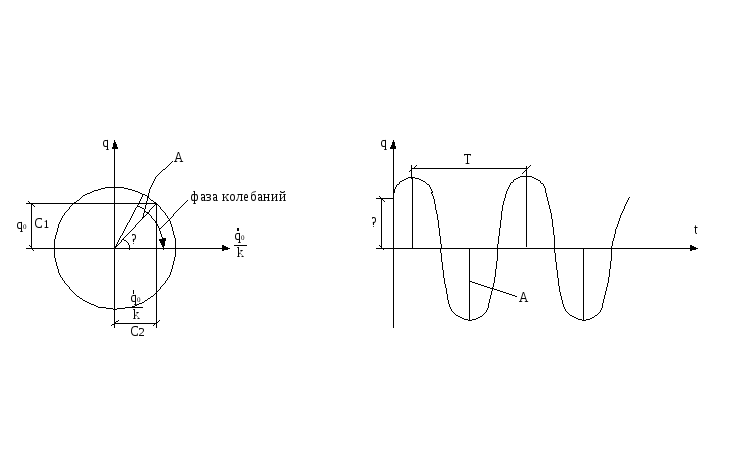
- решение дифференциального уравнения в амплитудной форме, где: А – амплитуда колебаний;

α – начальная фаза колебаний; k – частота колебаний; - фаза колебаний;

- период колебаний.

при t=0:

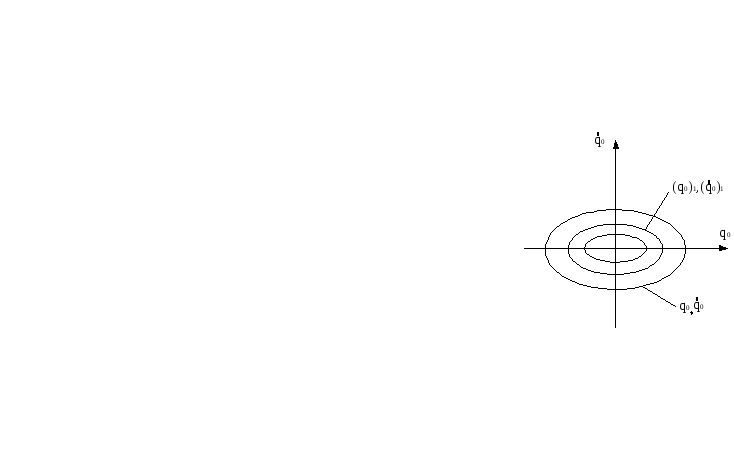
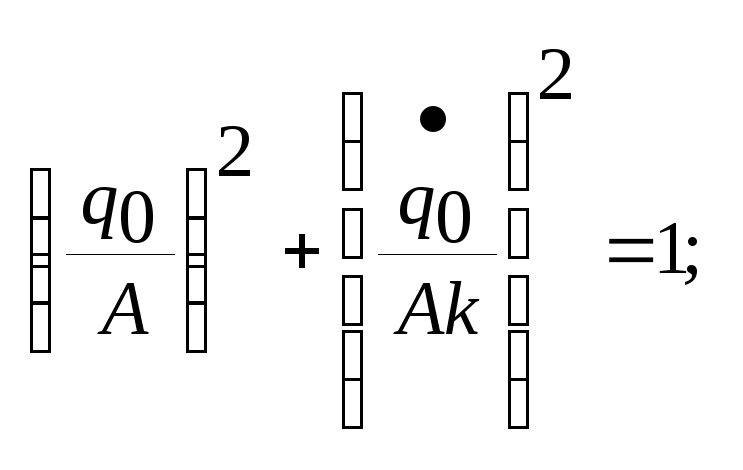- уравнение эллипса.

Графически можно интерпретировать как семейство эллипсов, построенных в фазовой плоскости

с осями q и q’. Если система совершает гармонические колебания, то эллипсы замкнуты, а их вид зависит от начальных условий.

Основные свойства малых свободных колебаний:

1. Они гармонические;

2. Амплитуда и начальная фаза определяются начальными условиями;

3. Точки системы движутся периодически, проходя положение равновесия;

4. Все точки системы движутся в одной фазе, одновременно достигая положения равновесия.

5. Малые свободные колебания изображаются семейством эллипсов в фазовой плоскости.

Содержание:

1.Предмет динамики. Масса материальной точки. Сила Закона динамики. Инерциальные системы отсчёта.

2.Теорема Штейнера-Гюйгенса-Эйлера о моментах инерции относительно параллельных осей. Примеры вычисления моментов инерции.

3.Дифференциальное уравнение движения свободной и несвободной материальной точки в координатной и естественной форме.

4.Теорема об изменении количества движения точки. Закон сохранения количества движения материальной точки.

5.Две задачи динамики. Пример решения первой задачи динамики.

6.Теорема о движении центра масс системы. Закон сохранения движения центра масс.

7.Вторая задача динамики. Постоянные интегрирования, их определение по начальным условиям.

8.Теорема об изменении количества движения системы. Закон сохранения количества движения системы.

9.Идеальные связи. Обобщённые силы. Вычисление обобщённых сил.

10.Теорема об изменении количества движения точки. Закон сохранения момента количества движения.

11.Относительное движение материальной точки. Дифференциальные уравнения относительного движения материальной точки. Переносная и Кориолисова силы инерции.

12.Теорема об изменении количества движения системы. Закон сохранения кинетического момента системы.

13.Частные случаи динамической теоремы Кориолиса. Принцип относительности классической механики.

14.Работа силы. Работа равнодействующей силы. Аналитическое выражение работы.

15.Работа силы тяжести. Работа упругой силы. Работа силы приложенной к телу, имеющему оси вращения.

16.Механическая система. Масса, центр масс системы. Внешние и внутренние силы системы. Момент инерции твёрдого тела относительно центра, оси, плоскости.

17.Момент инерции твёрдого тела относительно центра, оси, плоскости. Центробежные моменты инерции.

18.Понятие о радиусе инерции. Определение моментов инерции тел в простейших случаях.

19.Кинетическая энергия твёрдого тела в различных случаях его движения. Теорема об изменении кинетической энергии механической системы.

20.Потенциальное силовое поле. Потенциальная функция. Поверхность равного потенциала. Работа силы в потенциальном поле.

21.Потенциальная энергия. Закон сохранения механической энергии.

22.Связи и их уравнения. Квалификация связей. Обобщённые координаты. Возможные перемещения.

23.Приведение сил инерции к центру. Главный вектор и главный момент инерции.

24.Принцип Даламбера для материальной точки, для механической системы.

25.Принцип возможных перемещений. Пример.

26.Общее уравнение динамики.

27.Уравнение Лагранжа 2-ого рода.

28.Понятие об устойчивости механической системы. Теорема Лагранжа-Дирихле.

29.Собственные малые колебания системы. Амплитуда, период, начальная фаза колебаний. Явление резонанса.

30.Малые колебания механической системы с учётом линейного сопротивления.

31.Вынужденные колебания механической системы без учёта сил сопротивления.

32.Вынужденные колебания механической системы с учётом сил сопротивления.

33.Теория удара, общие положения. Ударный импульс.

34.Действие ударной силы на материальную точку. Теорема об изменении количества движения материальной точки при ударе.

35.Теорема об изменении кинетического момента механической системы при ударе.

36.Теорема об изменении количества движения механической системы при ударе.

37.Действие ударных сил на тело, вращающееся вокруг оси.

38.Удар тела о неподвижную поверхность. Линия удара, центральный, косой удар. Коэффициент восстановления при ударе.

39.Косой центральный удар.

40.Теорема Карно.

41.Равновесие системы тел.

42.Сложное движение точки. Модуль и направление ускорения Кориолиса.

43.Фермы. Определение усилий в стержнях фермы.

44.Плоскопараллельное движение твёрдого тела. Определение скорости точки тела в плоском движении методом полюса и методом МЦС.

=1=

Предмет динамики, масса материальной точки. Сила закона динамики. Инерциальная система отчета.

Динамика-раздел теор. мех., в которой изучают движение тел или систем тел с учетом их масс и под действием приложенных сил. Все задачи в динамики сводятся к рассмотрению 2-х задач:

1. прямая задача динамики- то есть по известным кинематическим параметрам определяют приложенные к этой точке силы.

x=x(t) x =a_x

y=y(t) y =a_y

z=z(t) z =a_z

md²x/dt²=F_x

md²y/dt²=F_y F√(F_x²+F²_y+F²_z)

md²z/dt²=F_z

2)Обратная задача динамики- когда по известной массе точки и действующей на точку сил определяют уравнение движения точки.

∑x_i=mx =0 x=C₁=0, x=C₁t+C₂

∑y_i=my =0 y=C₃, y=C₃t+C₄

∑z_i=-mg=mz  z=-gt+C_5, z=-gt²/2+C₅t+C₆

Масса материальной точки- это величина прямопропорциональная его весу и обратно ускорению свободного падения.

Материальная точка- это такая точка, размерами которой можно пренебречь.

Инерциальная система отчета- это система, в которой выполняется закон инерции. За инерциальную систему отчета принимают систему отчета связанную с Землей.

Система отчета- это система координат, по отношению к которой движется точка.

Сила- это мера механического взаимодействия тел, определяющее интенсивность и направление этого взаимодействия.

Постоянные силы F=const, направленные силы тяжести в близи поверхности земли.

Переменные силы зависят от положения точки F=f(r)- сила упругости

1. от времени F=f(t)

2. от скорости F=f(dr/dt)

Законы динамики:

1) Закон инерции: материальная точка находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока действие других тел не изменит его движение.

2) Закон пропорциональности силы и ускорения: ускорение материальной точки пропорционально силе, приложенной к ней и движется с ней в одинаковое направление.

3) Закон действия и противодействия или равенства: два тела взаимодействуют с силами равными по модулю и направленными вдоль одной прямой противоположно направлению

4) Закон независимости действия сил: если на точку действует система сил, то ускорение которое они ей сообщают равно геометрической сумме ускорений сообщаемых каждой из сил в отдельности.

=2=

Теорема Штейнера-Гюйгенса-Эйлера о моментах инерции относительно параллельных осей. Примеры вычисления моментов инерции.

Существует простая связь между моментами инерции тела относительно параллельных осей (теорема Гюйгенса-Штейнера), одна из которых проходит через центр масс.

Теорема. Момент инерции телаотносительно некоторой осиравен сумме момента инерциитела относительно осипроходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояний между осями: (1)

где М – масса тела, d – расстояние между двумя параллельными осями.

Пусть оси ипараллельны, причем осьпроходит через точку С – центр масс тела.

Возьмем начало координат в точке С, совместим ось z с осью , а осьу направим так, чтобы она пересекала оси и(рис.2.5)

Выделим в теле произвольный элемент массой dm и опустим из него перпендикуляры на оси z и , обозначив их соответственноh и

Согласно определению осевых моментов инерции моментов, будем иметь

По теореме косинусов (рис.2.5) найдем , однако, гдеу – координата элемента, тогда

Подставим полученное выражениев формулу (1), определяющую момент инерции

Первый интеграл равен по определению, второй – массе тела М, а третий – нулю: , поскольку начало координат совпадает с центром масс. Следовательно,

Получим формулы для вычисления моментов инерции некоторых простых тел.

Однородный стержень

Имеем однородный стержень длиной L и массой М. Вычислим момент инерции стержня относительно оси Сz, проходящей через центр масс стержня и перпендикулярной к нему (рис. 2.7).

Для этого нужно просуммировать все массы, умноженные на квадраты расстояния x до оси Cz. Тогда, согласно(2.7),  имеем

Если разделить стержень на отрезки длиной dx, то соответствующий элемент массы будет пропорционален dx (dmdx), а если бы dx составляло длину всего стержня, то его масса была бы равна М (ML). Поэтому

Вычисляя интеграл, получаем

Таким образом,

Размерность момента инерции всегда равна массе, умноженной на квадрат длины (кг м²), так что единственная величина, которую мы вычислили, это множитель 1/12.

Момент инерции стержня относительно оси , проходящей перпендикулярно стержню через его конец, параллельно zС, определяется по теореме Гюйгенса-Штейнера: , где

Следовательно

=3=

3.Дифференциальное уравнение движения свободной и несвободной материальной точки в координатной и естественной форме.

Дифференциальное уравнение движения материальной точки.

Рассмотрим движение материальной точки по отношению к инерциальной системе отсчёта под действием системы сил

-свободная материальная точка.

-несвободная материальная точка.

-эти 3 уравнения- дифференциальные уравнения движения

материальной точки в координатной форме.

-эти 3 уравнения- дифференциальные уравнения движения для

свободной материальной точки.

Проекция на оси естественного трёхгранника

- эти два уравнения – дифференциальные уравнения материальной

точки на оси естественного трёхгранника.

; - тангенсальная и нормальная составляющая ускорения.

ПОМЕТКА: на рисунке везде векторы, где Аr -и т. д.

=4=

Теорема об изменении кол-ва движения точки. Закон сохранения кол-ва движения МТ.

Кол-во движения точки ­­­- - одна из двух мер механического движения – импульс силы - характеристика действующих сил на точку за некоторый промежуток времени.

Элементарный импульс:

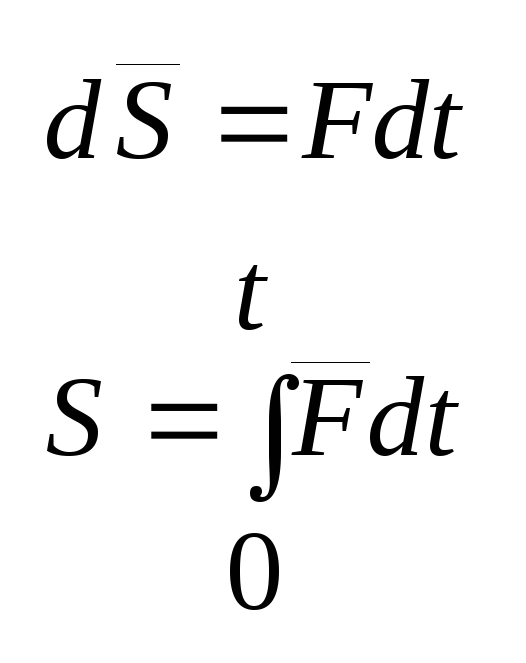
Второй закон Ньютона:

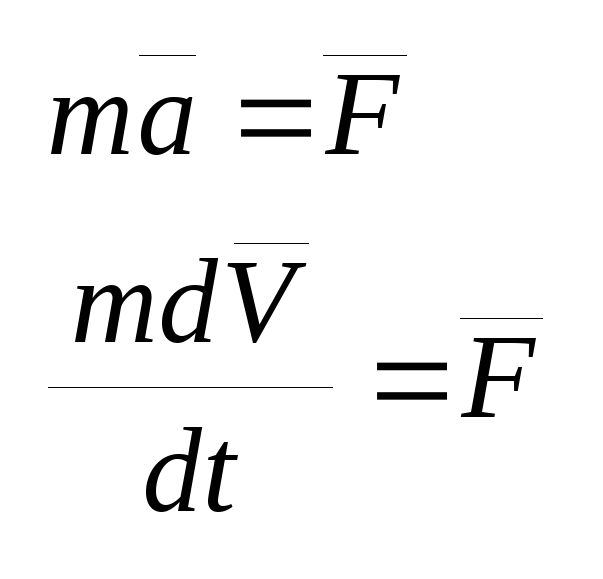
- теорема в дифференциальной форме.

Производная по времени от кол-ва движения точки равна силе ,действующей на точку.

- теорема в интегральной форме.

Изменение кол-ва движения точки за некоторый промежуток времени равно импульсу силы, действующей на точку за некоторый промежуток времени

Закон сохранения кол-ва движения:

Если , то

если , то и т. п.

=5=

5.Две задачи динамики. Пример решения первой задачи динамики.

Первая задача динамики:

Зная массу точки и уравнение её движения определяют силы действующие на точку.

Решается эта задача – дифференцированием.

Вторая задача динамики, основная и обратная:

По имеющимся и известной массе точки и действующей на точку силе определить уравнение движения точки.

Решается эта задача – интегрированием.

Пример решения первой задачи динамики:

Законы движения:

Затем дифференцируем эти уравнения:

, так как - по второму закону Ньютона , то

, значит общая сила действующая на эту точку равна:

, , где- единичный орт по оси х.

В естественной форме:

=6=

Теорема о движении центра масс

Известно, что твердое тело и механическая система в плоскости может двигаться достаточно сложно. К первой теореме о движении тела и механической системы можно прийти следующим образом: бросить к.-л. предмет, состоящий из множества скрепленных между собой твердых тел. Ясно, что он полетит по параболе. Это выявилось при изучении движения точки. Однако теперь объект не точка. Он поворачивается, покачивается в процессе полета вокруг некого эффективного центра, который движется по параболе. Первая теорема о движении сложных предметов говорит о том, что некий эффективный центр есть центр масс движущегося предмета. Центр масс не обязательно находится в самом теле, он может лежать и где-то вне его. Теорема. Центр масс механической системы движется как материальная точка массой равной массе всей системы, к которой приложены все внешние силы, действующие на систему

Для доказательства теоремы перепишем дифференциальные законы движения (3.3) в следующем виде:

(3.5)

где N – число точек системы.

Сложим почеленно уравнения между собой: (а)

Положение центра масс механической системы относительно выбранной системы координат определяется формулой (2.1): где М – масса системы. Тогда левая часть равенства (а) запишется (б)

Первая сумма, стоящая в правой части равенства (а), равна главному вектору внешних сил, а последняя по свойству внутренних сил равна нулю. Тогда равенство (а), с учетом (б) перепишется(3.6)т.е. произведение массы системы на ускорение центра ее массы равно геометрической сумме всех действующих на систему внешних сил.

Из уравнения (3.6) следует, что внутренние силы непосредственно не влияют на движение центра масс. Однако в ряде случаев являются причиной появления внешних сил, приложенных к системе. Так, внутренние силы, приводящие во вращение ведущие колеса автомобиля, вызывают действие на него внешней силы сцепления, приложенной к ободу колеса.

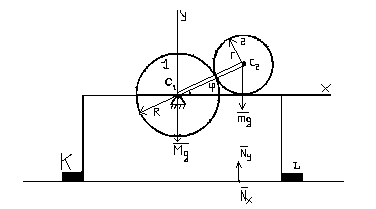
Пример 2. Механизм, расположенный в вертикальной плоскости, установлен на горизонтальной гладкой плоскости и прикреплен к ней жестко закрепленными с поверхностью брусками К и рис. 

Диск 1 радиусом R неподвижен. Диск 2 массой m и радиусом r скреплен с кривошипом , длиной R+r в точке С₂. Кривошип вращается с постоянной

угловой скоростью . В начальный момент кривошип занимал правое горизонтальное положение. Пренебрегая массой кривошипа, определить наибольшее горизонтальное и вертикальное усилия, действующие на бруски, если общая масса станины и колеса 1 равна М. Также рассмотреть поведение механизма при отсутствии брусков.

Решение. Система состоит из двух масс (N=2): неподвижного диска 1 со станиной и подвижного диска 2. Направим ось у через центр тяжести неподвижного диска по вертикали вверх, ось х – вдоль горизонтальной плоскости.

Запишем теорему о движении центра масс (3.6) в координатной форме (б)Внешними силами этой системы являются: вес станины и неподвижного диска – Mg, вес подвижного диска – mg, - суммарная горизонтальная реакция болтов, - нормальная суммарная реакция плоскости. Следовательно, (в)

Тогда законы движения (б) перепишутся

Вычислим координаты центра масс механической системы:

(г)

как видно из рис., , , (угол поворота кривошипа ), . Подставляя эти выражения в (г) и вычисляя вторые производные по времени t от , , получим, что (д)

Подставляя (в) и (д) в (б), находим

Горизонтальное давление, действующее на бруски, имеет наибольшее и наименьшее значения, когда cos=1 соответственно, т.е

Давление механизма на горизонтальную плоскость имеет наибольшее и наименьшее значения, когда sinсоответственно, т.е.

Фактически решена первая задача динамики: по известным уравнениям движения центра масс системы (д) восстанавливаются силы, участвующие в движении.

В условиях отсутствия брусков K и L рис, механизм может начать подпрыгивать над горизонтальной плоскостью. Это будет иметь место, когда , т.е. когда , отсюда следует, что угловая скорость вращения кривошипа, при которой происходит подпрыгивание механизма, должна удовлетворять равенству

Закон сохранения движения центра масс

Если главный вектор внешних сил, действующих на систему, равен нулю, т.е. , то из (3.6) следует, что ускорение центра масс равно нулю, следовательно, скорость центра масс является постоянной по модулю и направлению. Если, в частности, в начальный момент центр масс находится в покое, то он покоится в течение всего времени, пока главный вектор внешних сил равен нулю.

Из этой теоремы вытекает несколько следствий.

• Одними внутренними силами нельзя изменить характер движения центра масс системы.

• Если главный вектор внешних сил, действующих на систему, равен нулю, то центр масс находится в покое или движется равномерно и прямолинейно.

• Если проекция главного вектора внешних сил системы на некоторую неподвижную ось равна нулю, то проекция скорости центра масс системы на эту ось не изменяется.

• Пара сил, приложенная к твердому телу, не может изменить движение его центра масс (она может вызвать только вращение тела вокруг центра масс).

Рассмотрим пример, иллюстрирующий закон сохранения движения центра масс.

Пример 3. Два груза массами и соединены нерастяжимой нитью, переброшенной через блок, закрепленный на клине массой М. Клин опирается на гладкую горизонтальную плоскость. В начальный момент система находилась в покое. Найти перемещение клина по плоскости при опускании первого груза на высоту Н. Массой блока и нити пренебречь.

Решение. Внешними силами, действующими на клин вместе с грузами, являются силы тяжести , и Mg, а также нормальная реакция гладкой горизонтальной поверхности N. Следовательно,

Поскольку в начальный момент система находилась в покое, имеем .Вычислим координату центра масс системы при и в момент t₁, когда груз весом g опустится на высоту H.

Для момента : где , , х – соответственно координаты центра масс грузов весом g, g и клина весом Мg.

Предположим, что клин в момент времени переместится в положительном направлении оси Ox на величину L, если груз весом опустится на высоту Н. Тогда, для момента

т.к. грузы вместе с клином передвинутся на L вправо, a груз переместится на расстояние по клину вверх. Так как , то после вычислений получим, откуда

.

=7=

Вторая задача динамики. Постоянные интегрирования, их определения по начальным условиям.

По имеющийся известной массе точки и действующей на точку сил определить уравнение движения точки.

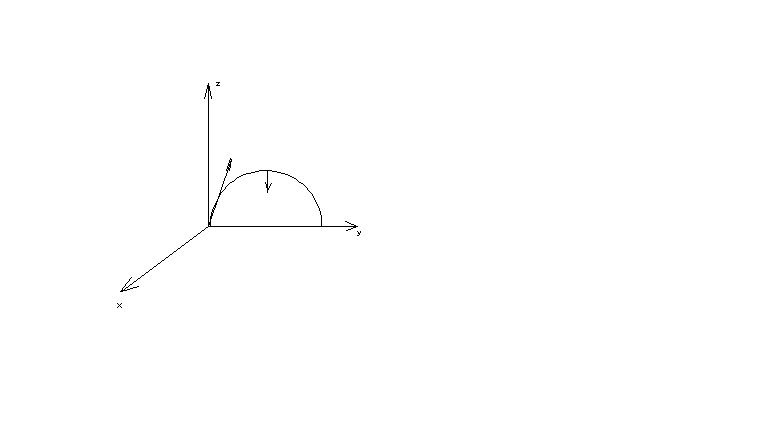
∑x_i=mx =0; x=C₁=0, x=C₁t+C₂ ∑y_i=my =0; y=C₃, y=C₃t+C₄

∑z_i=-mg=mz; z=-gt+C_5, z=-gt²/2+C₅t+C₆

1) при t=0 x₀=C₁=0

x₀=C₂=0

2) y₀=V₀cosα=C₃

y₀=C₄=0

3) z₀ = V₀sinx=C₅

z₀=C₆=0

y=V₀cosαt уравнение траектории

z=-gt² / 2+V₀sinαt в параметрическом виде

t=y / V₀cosα

z= - g (V₀cosα)² / 2+V₀sinx

z= -g/2 (y/ V₀cosα)²+ V₀sinαy / V₀cosα

z=f(y)

=8.=

Теорема об изменении кол-ва движения системы. Закон сохранения кол-ва движения системы.

К- кол-во движения системы.

- теорема в дифференциальной форме

Проинтегрируем:

- теорема в интегральной форме.

Изменение кол-ва движения системы за некоторый промежуток времени равно сумме импульсов всех внешних сил, действующих на точку, и системы за тот же промежуток времени.

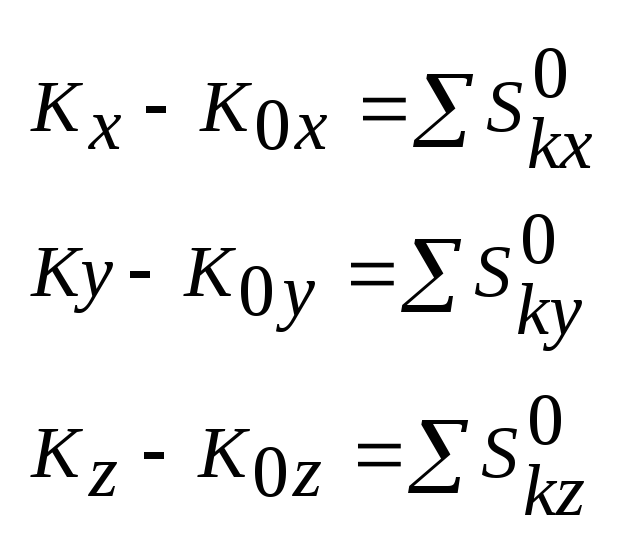
Следствие(Закон сохранения):

если,то

если,то и т. п.

Эта теорема лежит в основе расчетов по гидроаэродинамике, теории удара.

=9=

Идеальные связи.Обозначим силы реакций связей системы .

Связи системы называются идеальными, если сумма элементарных работ реакций этих связей на любых возможных перемещениях всегда равна нулю, т. е.

(4.1)

Приведем примеры идеальных связей:

1. В абсолютно твердом теле точки связаны идеальными связями. Силами реакций связей в этом случае являются внутренние силы, для которых было доказано, что сумма элементарных работ этих сил на любом возможном перемещении, равна нулю.

2. Абсолютно гладкая поверхность является идеальной связью для точки. Возможные перемещения точки направлены по касательной к поверхности, а силы реакции в этом случае направлены по нормали к ним, т.е. перпендикулярны перемещениям, см. рис.11, следовательно, элементарная работа силы реакции на перемещении равна нулю.