1.14. Равновесие при наличии трения.

Если тело находится в равновесии на шероховатой поверхности, полная реакция такой опорной поверхности будет представлена двумя составляющими: нормальным давлениеми силой трения(рис. 38). Величина предельной силы трения не зависит от размеров соприкасающихся поверхностей:

(14.1)

где - коэффициент трения скольжения, зависящий от материала и состояния соприкасающихся поверхностей. В уравнения равновесия твердого тела, находящегося на шероховатой поверхности, кроме сил заданных и реакций связей будет входить сила трения.

Пример №5.

Станок весом передвигают по деревянному настилу с углом подъемапри помощи лебедки (рис.39). Определить натяжение троса, если коэффициент трения стали по дереву.

Решение:

1. Рассматриваем равновесие станка, находящегося на наклонной плоскости под действием силы тяжести , натяжением троса, составляющих реакций шероховатой поверхностии. При равномерном подъеме все эти силы должны находиться в равновесии. Величину нормального давления определим, проецируя все силы на осьY:

откуда

2. Уравнение равновесия тела составляем в проекции на ось X:

откуда

1.15. Равновесие при наличии трения качения.

При перекатывании одной криволинейной поверхности по дру­гой возникает сопротивление, называемое трением качения. Если к катку приложить силу (рис. 40 ), то вследствие деформа­ции поверхности в месте контакта линия действия силы нормально­го давления проходит на некотором расстоянии К от оси Максимальную величину К, соответствующую предельному положению равновесия, называют коэффициентом трения качения. Силы и образуют пару сил, стремящуюся повернуть каток. Силы и образуют пару сил с моментом, препятствующим повороту кат­ка. Момент этой пары

( 15.1 )

называют моментом трения качения. Трение качения возникает только при перекатывании упругих тел. Для качения абсолютно твердого катка по абсолютно твердой не деформируемой поверх­ности не потребуется никакой силы.

Если , то скольжение невозможно,

если ,то проходит одновременно скольжение и качение,

если , то качение невозможно.

Пример №6.

Д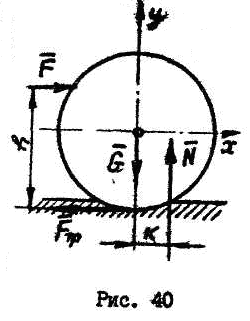ля равномерного передвижения по горизонтальному деревянному настилу станка (рис. 41) весом использовали 10 стальных катков диаметром и весомкаждый. Определить необходимое горизонтальное движущее усилие , если коэффициент трения качения стали по чугуну, а стали по дереву.

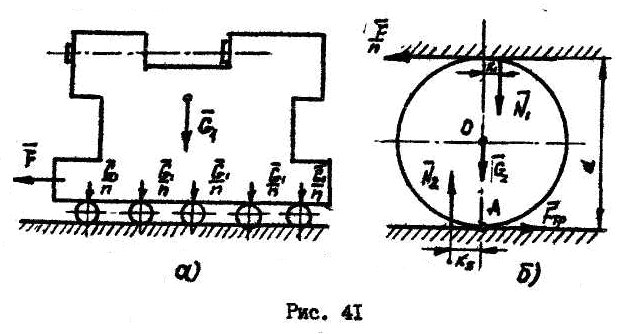
Решение:

1. Считаем, что на каждый каток приходится одинаковая часть веса станины . Рассматриваем равновесие одного катка (рис. 41,б) под действием активных сил и реакций связей: силы тяжести, нормальных реакцийи, движущей силына один каток и силы трения скольжения со стороны пола. Составим уравнение равновесия:

(1)

(2)

где (3)

(4)

Подставим (3) и (4) в (1):

1.16. СТАТИЧЕСКИ ОПРЕДЕЛЕННЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛЕННЫЕ ЗАДАЧИ.

Для каждого случая нагружения твердого тела можно составить определенное число независимых уравнений. Если числа уравнений достаточно для определения неизвестных величин, система называется статически определимой, в противном случае – статически неопределимой. Если арка (рис.42) нагружена силами , то направления реакций в опорахА и В неизвестны, каждая из них будет представлена двумя составляющими. Следовательно, количество неизвестных () превышает число независимых уравнений равновесия для плоской системы сил, т.е. плоская система является статически неопределимой.