2.10. Вращение тела вокруг неподвижной точки.

Всякое элементарное перемещение тела, имеющего неподвижную точку (рис.119), представляет собой элементарный поворот вокруг некоторой мгновенной оси вращения , проходящей черев эту точку.

Скорости всех точек, лежащих на мгновенной оси вращения, равны нулю. Положение мгновенной оси вращения в пространстве и в самом теле постоянно изменяется.

Вектор мгновенной угловой скорости направлен вдоль мгно­венной оси вращения. Со временем вектор мгновенной угловой ско­рости изменяется как по величи­не, так и по направлению (рис.120). Мгновенное угловое ускорение определяет изменение угловой скорости по величине и направлении:

(2.53)

Вектор мгновенного углового ускорения направлен по касательной к кривой , являющейся годог­рафом вектора мгновенной угловой скорости.

Скорость любой точки тела пропорциональна расстоянию этой точки до мгновенной оси вращения (рис.121):

, (2.54)

где - мгновенная скорость колеса;

- радиус-вектор, определяющий положение точки относительно неподвижной точки.

Ускорение точ5ки состоит из вращательной и осестремительнойсоставляющих:

, (2.55)

, , (2.56)

где - расстояние от точкидо вектора;

- расстояние от точкидо мгновенной оси вращения (рис.122).

Вектор осестремительного ускорения направлен перпендикулярно мгновенной оси вращения. Векторвращательного ускорения направлен перпендикулярно плоскости, проходящей через точкуи вектор.

Пример №27.

Найти скорости точек и конического катка (бегуна), катящегося без скольжения по горизонтальной конической опоре, если точка лежит на окружности радиуса , расстояние . Скорость движения центра катка по его траек­тории постоянна и равна (рис.123).

Решение:

1. Мгновенная ось вращения проходит через две неподвиж­ные точки и . Сферическое движение катка можно рассмат­ривать как вращение вокруг мгновенной оси .Скорость лю­бой точки тела при таком движении пропорциональна расстоянию до мгновенной оси вращения. Так как скорость точки известна, можно определить

мгновенную угловую скорость:

,

где ;.

2. Определим угловую скорость собственного вращения катка , которая является угловой скоростью относительного движения:

.

Каток участвует в переносном вращательном движении вокруг оси с угловой скоростью.

Определим скорость точки :

;

.

Скорость точки равна нулю, так как точка находится на мгновенной оси вращения.

3.Ускорение точки состоит из вращательной и осестремительной составляющих:

(1)

где .

Вектор направлен перпендикулярно мгновенной оси вращения по отрезку, составляющему.

2.11. Общий случай движения свободного

ТВЕРДОГО ТЕЛА.

Свободное твердое тело имеет 6 степеней свободы и может перемещаться как угодно в пространстве по отношению к некоторой

неподвижной системе отсчета.

Л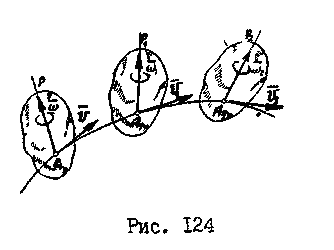юбое элементарное пе­ремещение свободного твердого тела слагается из элементар­ного поступательного перемещения вместе с полюсом и элементарного поворота вокруг мгновенной оси вращения ,проходящей через этот полюс (рис.124). Любая точка тела участвует в сложном движении: относительном вращательном движении вместе с телом вокруг по­люса и в переносном поступательном движении вместе с полюсом . Скорость точки определяется геометрической суммой (рис.125):

, (2.57)

,

,

где - расстояние до мгновенной оси вращения;

Ускорение точки также определяется геометрической суммой:

, (2.58)

Где ,

.