2.7. Механические передачи.

Передача движения от одной машины к другой или внутри машины от одного ее вала к другому осуществляется разнообразными механизмами, называемыми механическими передачами. Переда­ча движения может осуществляться:

а) гибкой связью (ременные, цепные передачи);

б) непосредственным контактом (фрикционные, зубчатые передачи).

Валы и шкивы, от которых передается движение, называются ведущими, воспринимают движение ведомые валы и шкивы.

Ременная передача между параллельными валами шкет быть открытой (рис.74,а) или перекрестной (рис.74,б). Перекрестная передача позволяет изменить направление вращения.

При отсутствии проскальзывания все точки ремня движутся с одинаковой скоростью:

,

откуда можно получить соотношение между кинематическими харак­теристиками и размерами вращающихся звеньев:

.

Фрикционными называются устройства, передача вращательного движения в которых осуществляется за счет трения. Передача вращения между параллельными валами может осуществляться цилиндрическими колесами (рис.75,а), а между валами с пересекающими осями (рис.75,б) - коническими колесами. Кинематические характеристики и размеры фрикционных колес свя­заны между собой соотношением:

. (2.37)

С помощью вариатора (рис.75,в) можно путем перемещения колеса вдоль диаметра колеса получить переменное соотношение меж­ду кинематическими характеристиками и размерами звеньев:

(2.38)

где -переменное расстояние средней плоскости колеса от

оси колеса ;

- радиус колеса .

Зубчатые передачи являются одними из самых распространенных типов передаточных механизмов (рис.76,77,78,79). Скорость точ­ки можно выразить через угловые скорости и размеры колес:

.

Так как число зубьев пропорционально размеру колес, можно полу­чить следующие соотношения:

. (2.39)

При внешнем зацеплении (рис.77,а) колеса вращаются в противо­положных направлениях, при внутреннем зацеплении (рис.77,б) -направление вращения совпадает. Конические зубчатые колеса (рис.78) служат для передачи вращения между пересекающимися валами.

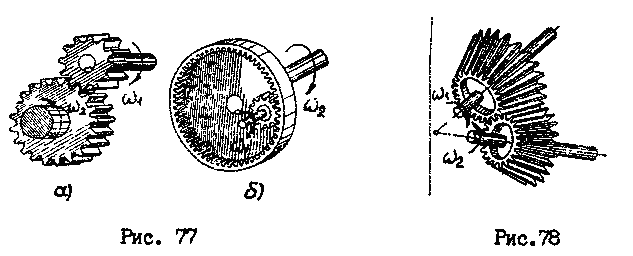
Для преобразования вращательного движения в поступательное при­меняют реечное зацепление (рис,79).

Скорость поступательно движущейся рейки равна скорости точки контакта и может быть определена по формуле:

Многоступенчатой передачей называется механизм, содержащий ряд простых передач (рис. 80). Для всей передачи от ведущего вала и валуможно установить следующие соотношения:

(2.30)

Пример № 7.

Дисковая пила (рис.81) диаметром приводится в движение от электродвигателя ременной передачей, шкивы которой имеют размеры и.С какой угловой скоростью должен вращаться шкив электродвигателя, чтобы скорость зу­бьев пилы не превышала ?

1.Линейная скорость зубьев пилы пропорциональна угловой скорости пилы и шки­ва :

,

откуда .

Шкив насажен на один вал с пилой, следовательно, угловая скорость шкива равна .

2. Шкивы и соединены бесконечным ремнем. Выразим соотношение между угловыми скоростями шкивов и их размерами:

, откуда ,

что соответствует частоте вращения:

.

ПРЕОБРАЗОВАНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА В МЕХАНИЗМАХ.

Пример №8.

Механизм состоит из ступенчатых колес и ,связанных ременной передачей, колеса и находятся в зацеплении, колесо находится в зацеплении с зубчатой рейкой ,груз находится на конце нити, намотанной на шкив радиуса (рис. 82). Опреде­лить скорости точек и , ускорение груза ,ускорение точ­ки и угловое ускорение колеса в момент времени ,если задан закон движения рейки и размерыколес:

, ,,,

, .

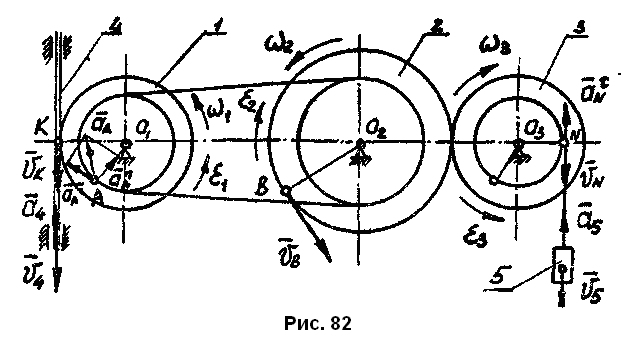
Решение:

1. Рейка совершает поступательное движение по закону . Определим скорость движения рейки:

. При ,.

Ускорение рейки: .

Знак минус указывает, что рейка движется замедленно.

2. Точка , лежащая на ободе колеса, движется со скоростью, равной скорости рейки, находящейся в зацеплении с колесом, т.е.

.

Учитывая, что , можно выразить угловую скорость колеса:

.

Угловое ускорение колеса :

.

Колеса радиусов инаходятся на одном валу. Определим ускорение точки:

,

где ,,

3. Колеса радиусов исвязаны бесконечным ремнем, поэтому скорости всех точек ремня одинаковы, т.е., угловые скорости и угловые ускорения валовиобратно пропорциональны

размерам колес:

;;

;.

Скорость точки , лежащей на ободе колеса:

.

4. Колеса радиусов инаходятся в жестком зацеплении друг с другом, поэтому

;;

;.

Скорость точки , лежащей на ободе колесарадиуса:

.

5. Ускорение груза равно касательному ускорению точки:

.

Для заданного момента времени :

;

;

;

;

.