2.5. Поступательное движение твердого тела.

Поступательным называется такое движение твердого тела, при котором всякая прямая, неизменно связанная с этим телом, при движении остается параллельной своему начальному положению

(рис. 66).

П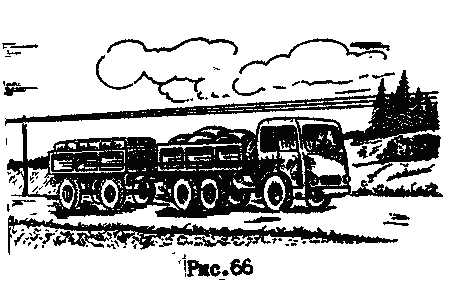ри поступа­тельном движении точки тела могут двигаться как по прямолинейным, так и по криволиней­ным траекториям.

На рис.67 спарник , соединяющий кривошипы и ,совершает поступательное движение, а его точки и движутся по окружностям. Любая прямая, проведенная по подвес­ной кабине вертикального коле­са обозрения (рис. 68), во время вращения колеса остается параллельной

самой себе. Сле­довательно, подвесные кабины совершают поступательное дви­жение по окружности.

При поступательном дви­жении тела все его точки дви­жутся по одинаковым (при нак­лонении совпадающим) траекто­риям и имеют в каждый момент времени одинаковые по модулю и направлению скорости и уско­рения.

Так как все точки тела при поступательном движении дви­жутся одинаково, то поступательное движение тела вполне опреде­ляется движением какой-либо одной его точки. Таким образом, за­дача изучения поступательного движения твердого тела сводится к задаче кинематики точки.

Уравнениями поступательного движения твердого тела явля­ются уравнения движения любой точки тела. Например, для спарника (рис.67) уравнениями движения будут:

, ,(2.26)

Скорость и ускорение, общие для всех точек поступательно движущегося тела, являются скоростью и ускорением этого тела.

Пример №5.

От кривошипа 1 с помощью ползуна 2 приводится в поступательное движение кулиса 3 (рис.69) по закону . Определить скорость точкикулисы в момент времени.

Решение:

Так как при поступательном движении кулисы ее точки движутся одинаково, скорости точекиравны между собой. Зная закон движения точки, можно найти скорость:

.

При ,.

2.6. Вращение тела вокруг неподвижной оси.

Вращательным называется такое движение твердого тела, при котором все его точки, лежащие на прямой, называемой осью вращения, остаются неподвижными.

Если тело закрепить в двух точках (например, при помощи подшипника и подпятника), то прямая, проходящая через эти точки, и будет осью вращения. Кинематическими характеристиками вращательного движения тела являются угол поворота(рис.70), угловая скоростьи угловое ускорение.

При вращении тела вокруг оси угол поворотатела изменяется с течением времени:

(2.27)

Уравнение (2.27) является уравнением вращательного движения тела. Угол поворота тела измеряется в радианах.

Величина, характеризующая изменение угла поворота тела с течением времени, называется угловой скоростью.

Угловая скорость тела равна производной от угла по времени:

. (2.28)

Угловая скорость считается положительной, если направление вращения тела противоположно движению часовой стрелки. Следовательно, знак угловой скорости указывает направление вращения тела. Угловая скорость измеряется в радианах в секунду. Единица угловой скорости обозначается так:

или или

В технике угловую скорость тела часто выражают в оборотах в минуту . Зависимость междуиопределяется соотношением:

(2.29)

Величина, характеризующая изменение угловой скорости тела с течением времени, называется угловым ускорением. Угловой ускорение тела в данный момент времени равно первой производной от угловой скорости тела по времени или второй производной по времени от угла поворота:

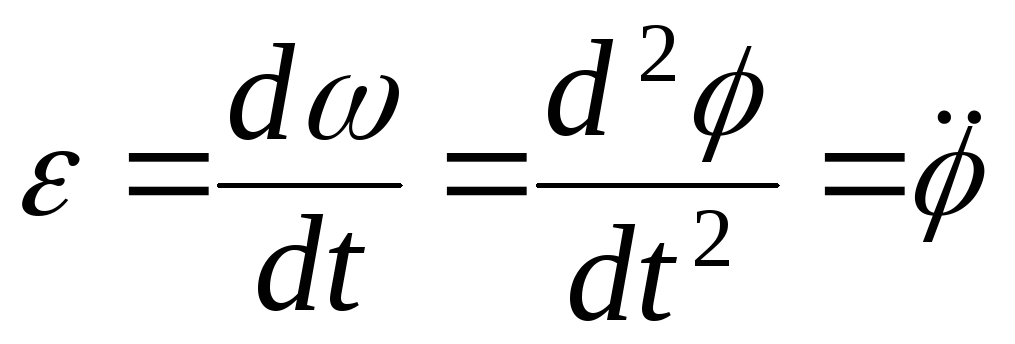(2.30)

Угловое ускорение тела измеряется илиили.

Если модуль угловой скорости с течением времени возрас­тает, вращение тела является ускоренным, а если убывает - за­медленным. 3нак угловой скорости определяет направление враще­ния.

Угловую скорость и угловое ускорение тела можно изобра­зить векторами, направленными вдоль оси вращения (рис, 71).

Вектор угловой скорости тела направлен вдоль оси вращения так, чтобы глядя с его конца, видеть вращение тела в направлении, противоположном движению часовой стрелки. При ус­коренном вращении тела направления векторов и совпа­дают (рис.71,а).

Любая точка вращающегося тела, не лежащая на оси враще­ния, движется по окружности в плоскости, перпендикулярной оси вращения. Скорость точки пропорциональна расстоянию точки до оси вращения и зависит от угловой скорости тела (рис.72).

(2.31)

Вектор скорости точки вращающегося тела направлен перпендику­лярно к радиусу, соединяющему точку с осью вращения. Иными сло­вами, вектор скорости направлен по касательной к траектории точки в сторону вращения.

Скорость точки, лежащей на оси вращения, равна нулю. Так как точка вращающегося тела движется, по криволинейной траектории, ус­корение точки будет представлено нормальной и касательной сос­тавляющими (рис.73):

(2.32)

Нормальное ускорение характеризует изменение скорости точки по направлению, зависит от радиуса кривизны траектории, т.е. рас­стояния точки до оси вращения:

. (2.33)

Касательное ускорение характе­ризует изменение модуля скорости точки вращающегося тела с течени­ем времени, зависит от углового ускорения тела и расстояния точки до оси вращения:

(2.34)

Модуль ускорения точки вращающегося тела можно определить по формуле:

. (2.35)

Связь между кинематическими характеристиками поступательного и вращательного движения твердого тела представлена в табл.2.

Таблица 2

Кинематические характеристики и вид движения		Поступательное движение тела		Вращательное движение тела
Уравнение движения	Общая формула Равномерное движение Равномерное переменное движение
Скорость	Общая формула Равномерное движение Равномерно переменное движение Размерность	Линейная		Угловая
Ускорение	Общая формула Равномерно переменное движение Размерность	Касательное		Угловое

Пример №6.

Ротор электромотора вращается с угловой скоростью . После выключения он делает до полной остановкиоборотов. Считая вращение ротора равнозамедленным, найти время вращения ротора до полной остановки, закон вращательного движения, угловую скорость и угловое ускорение ротора за время торможения.

Решение:

Для равнопеременного вращательного движения уравнение изменения кинетических параметров имеют вид:

; (1)

До полной остановки ротор повернется на угол :

.

В момент начала торможения ротор имел начальную угловую скорость:

.

В конце торможения угловая скорость ротора равна нулю:

; ;;

;

.

Время торможения ротора:

.

Угловое ускорение:

.

Подставив значения начальной угловой скорости и углового ускоренияв (1), получим закон изменения угловой скорости и угла поворота ротора в зависимости от времени:

.