10. Теорема об изменении момента количества движения.

Количество движения материальной точки является величиной векторной, для которой можно определить момент относительно центра или оси:;. (10.1) Производная по времени от момента количества движения точки относительно центра или оси равна моменту действующей силы относительно того же центра или оси:, (10.2). (10.3)

Момент количества движения называют еще кинетическим моментом. Кинетический момент точки приложен в точке О, относительно которой он определяется (рис. 28).

Если момент силы, приложенной к точке, относительно какого-либо центра или оси равен нулю, то кинетический момент точки относительно этого центра или оси остается постоянным. Если , то;

Если , то. (10.4)

ПРИМЕР 15.

Гирька М привязана к концу нерастяжимой нити (рис. 29), часть которой ОА пропущена через вертикальную трубку; гирька движется вокруг этой трубки по окружности радиуса МС=R, делая n₀=120об/мин. Медленно втягивая нить ОА в трубку, укорачивают наружную часть до длины ОМ₁, при котором гирька описывает окружность радиуса R₁=0,5R. Сколько оборотов в минуту делает гирька по этой окружности?

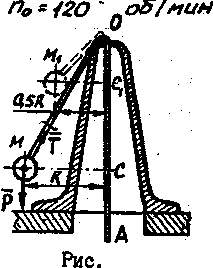
РЕШЕНИЕ.

1. Применим теорему об изменении кинетического момента относительно оси. Принимаем гирьку за материальную точку, и приложим к ней силу тяжести и реакцию связи – натяжение нити. Так как силапараллельна осиz, а сила пересекает эту ось, то, следовательно, кинетический момент точки относительно осиz будет оставаться постоянным. Согласно (10.4) .

2. В начальный момент времени гирька двигалась по окружности радиуса R, совершая n₀=120об/мин. Определим кинетический момент гирьки относительно оси z, обозначив массу гирьку m и предварительно выразив скорость гирьки через число оборотов , тогда. При втягивании нити радиус уменьшился доR₁=0,5R, а кинетический момент относительно оси остался постоянным. Следовательно, , откудаоб/мин.

Для механической системы кинетический момент (или главный момент количества движения системы относительно какого-либо центра или оси) равен сумме кинетических моментов точек системы относительно того же центра или оси ;

. (10.5)

Для вращающегося твердого тела кинетический момент относительно оси вращения равен произведению угловой скорости на его момент инерции относительно оси вращения.

. (10.6)

Момент инерции является мерой инертности для вращающихся тел. Моментом инерции механической системы из n точек относительно произвольного центра или оси называется сумма произведений масс этих точек на квадраты их расстояний до соответствующего центра или оси, т.е. ; (10.7)

. (10.8)

Рисунок 30

Для тел сложной геометрической формы вводится понятие радиуса инерции, т.е. расстояния до точки, где нужно сосредоточить массу тела, чтобы момент инерции этой точки относительно какого-либо центра или оси был равен моменту инерции тела относительно того же тела или оси. . (10.9)

Теорема Гюйгенса-Штейнера устанавливает зависимость между моментами инерции относительно параллельных осей:

момент инерции твердого тела или механической системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс плюс произведение массы на квадрат расстояния d между осями . (10.10)

Для однородного стержня длиной (рис. 31) моменты инерции относительно центра и оси определяют по формулам:

Рисунок 31

; (10.14)

. (10.12)

Формула (10.12) наглядно иллюстрирует изменение теорему

Штейнера: .

К точкам механической системы приложены внешние и внутренние силы.

Первая производная по времени от кинетического момента системы относительно произвольного центра или оси равна сумме моментов внешних сил, действующих на систему относительно того же центра или оси (теорема об изменении кинетического момента).; (10.13)

. (10.14)

Если момент внешних сил системы относительно произвольного центра или оси равен нулю, то кинетический момент системы относительно того же центра или оси остается постоянным:

1. Если , то.

2. Если , то. ()

Моменты инерции некоторых простейших тел приведены в таблице 1.

Рисунок 32

Рисунок 33

Е

Если человеку с гирями, находящемуся на горизонтальной платформе Жуковского (рис. 32), которая может вращаться вокруг вертикальной оси почти без трения, сообщить угловую скорость вращения вокруг этой оси, то , так как внешние силы или параллельны оси (силы веса человека, гирь и платформы), или пересекает ось (реакции подшипника при отсутствии силы трения). Если человек увеличит момент инерции относительно оси вращения, разводя руки с гирями в сторону, то угловая скорость вращения уменьшится, и наоборот.

Человек, стоящий на идеально гладкой горизонтальной плоскости (рис. 33), может повернуться вокруг оси, проходящей через центр тяжести перпендикулярно к этой плоскости, если начнет вращать руку над головой; направление вращения человека будет противоположно направлению вращения руки, так как .

Задачи на применение теоремы об изменении кинетического момента удобно решать в следующей последовательности:

1. выбрать систему отсчета, совместив одну из осей с осью вращения;

2. показать все внешние силы, приложенные к системе;

3. выразить кинетический момент относительно выбранной оси или центра;

4. используя теорему об изменении кинетического момента, определить искомые величины.

сли тело весомвращается вокруг вертикальной оси (рис. 32), то, следовательно,.

ПРИМЕР 16.

Однородная круглая платформа радиусом R=1м, массой m₁=20кг вращается с угловой скоростью=10с^-1 вокруг вертикальной оси, отстоящей от центра платформы на расстоянии ОС=в=0,5R (рис. 34). В момент времени t₀=0 по желобу платформы начинает двигаться под действием внутренних сил груз D массой m₂=8кг по закону S=AD=5t², где S— в метрах, t— в секундах. Одновременно начинает действовать пара сил с моментом М=10кНм. Определить, пренебрегая массой вала, угловую скорость платформы как функцию времени.

Рисунок 35

Рисунок 34

РЕШЕНИЕ.

1. Рассмотрим механическую систему, состоящую из платформы и груза D. Применим теорему об изменении кинетического момента системы относительно оси z:. (1) Покажем все внешние силы, действующие на систему: весаи, реакции подшипникаи подпятника, пару сил с моментом М.

2. Кинетический момент системы относительно оси вращения найдем как сумму кинетических моментов платформы и груза . (2) Кинетический момент платформы, где-- момент инерции относительно оси вращения. Для нахождения момента инерции платформы используем формулу Штейнера:. Тогда. (3) Кинетический момент определяем, учитывая, что груз совершает сложное движение; абсолютная скорость грузаскладывается из переноснойи относительнойскоростей (рис. 35), т.е. .

В относительном движении груз движется по платформе по закону S=5t² . Тогда . Вектор относительной скорости груза направлен вдоль желоба в сторону, соответствующую возрастанию относительной координатыS=AD (рис. 35).

Переносным движением для груза является вращение платформы вокруг оси z.

, где . Кинетический момент груза относительно оси вращения выразим, используя теорему Вариньона;

;

где ;

,

тогда

. (4) Подставим (3), (4) в (2): . (5)

3. К системе приложена пара сил с моментом М=10t. Тогда уравнение (1) примет вид . (6) Разделяя переменные и интегрируя (6), получаем. (7) Подставим (7) в (5):

. (8) Постоянную интегрирования С₁ определяем из начальных условий. Если t=0, , то;. С учетом найденного значения постоянной интегрирования из уравнения (8) выразим угловую скорость платформы. С учетом заданных числовых значений получим.