5. Прямолинейые колебания точки.

Собственные колебания точки происходит под действием восстанавливающей силы , направленной к положению равновесия и пропорциональной расстоянию от этого центра (рис. 8). Проекция силына ось х равнаF_x=-cx. (5.1)

Дифференциальное уравнения движения точки М под действием силы имеет вид

, (5.2)

где с—коэффициент пропорциональности.

Если -- сила упругости пружины, коэффициент с называется жесткостью пружины. Размерность жесткости --. Жесткость пружины показывает, какую силу в Н необходимо приложить к пружине, чтобы растянуть (или сжать) ее на единицу длины (1м.).

Дифференциальное уравнение собственных колебаний точки имеет вид

; (5.3)

где -- циклическая частота.

Общее решение дифференциального уравнения (5.3) можно представить в виде

, (5.4)

где С₁, С₂—постоянные интегрирования, определяемые из начальных условий

, (5.5)

Общее решение дифференциального уравнения собственных колебаний в амплитудной форме

, (5.6)

где А—амплитуда колебаний;

-- начальная фаза.

, (5.7)

. (5.8)

Период колебания . (5.9)

График собственных колебаний точки изображен на рис. 9.

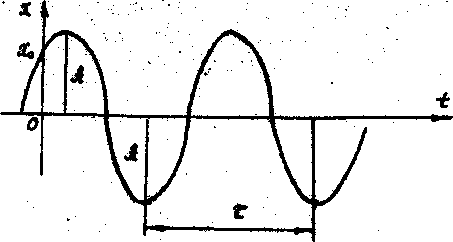
Рисунок 9

Колебания груза, подвешенного на пружине.

В недеформированном состоянии пружина имеет длину l (рис. 10). Если к концу пружины подвесить груз, пружина растянется на длину, где-- статическое удлинение пружины, зависящее от веса груза и упругих свойств пружины.

Колебания груза могут начаться только при не равных нулю начальных условиях, так как амплитуда колебаний зависит от х₀ и V₀ (см. уравнение (5.7)). Если начало координат поместить в положение статического равновесия – точку О, а затем вывести груз из положения равновесия, растянув пружину до длины l₀ и сообщить грузу начальную скорость V₀, то в произвольный момент времени деформация пружины . Дифференциальное уравнение движения груза в проекции на ось х имеет вид:

(5.10)

или . (5.11)

Так как , уравнение (5.11) имеет вид, т.е. действие постоянной силыне изменяет характера колебательного движения (см. уравнение (5.2)).

Если груз прикреплен к двум пружинам с жесткостью С₁ и С₂, то их заменяют одной пружиной с эквивалентной жесткостью, зависящей от соединения пружин. При последовательном соединении пружин (рис. 11)

.(5.12)

При параллельном соединении пружин (рис. 11)

. (5.13)

Если на точку кроме восстанавливающей силы (рис. 12) действует сила линейного сопротивления

, то дифференциальное уравнение движения точки будет . (5.14)

Рисунок 11

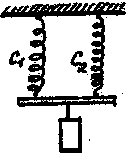
Если ,, гдеn – коэффициент сопротивления, то общее решение дифференциального уравнения

(5.15)

зависит от соотношения между коэффициентами k и n.

1. В случае малого сопротивления при n<k точка совершает затухающие колебания по следующему закону

, (5.16)

или , (5.17)

где С₁, С₂ или А, -- постоянные интегрирования, определяемые из начальных условий С₁=х₀; ; (5.18)

; . (5.19)

Период затухающих колебаний . (5.20)

Убывание амплитуды затухающих колебаний определяется декрементом

. (5.21)

График затухающих колебаний располагается между двумя огибающими: и(рис. 13).

Рисунок 13

2. При n>k имеем случай большого сопротивления, точка совершает апериодическое (непериодическое) затухающее движение согласно уравнению

, (5.22)

где .

Рисунок 13

П

1. ;>0;

2. >0; ;

3. >0; <0.

остоянные интегрирования определяются из начальных условий. Координата х убывает в соответствии с экспотенциальным законом, характер убывания зависит от начальных условий (рис. 14)

Во всех трех случаях движение быстро затухает.

3. При n=k будет случай критического (предельного) сопротивления. Точка совершает затухающее апериодическое движение по закону

(5.23)

или после определения постоянных интегрирования

. (5.24)

Характер затухания зависит от начальных условий (рис. 14).

ПРИМЕР 7.

Груз весом Р=98н подвешен к нижнему концу вертикальной пружины, верхний конец которой закреплен неподвижно (рис. 15). Жесткость пружины с=2,5н/см, а длина ее в недеформированном состоянии равна l=60см. Выбрав начало координат в положении статического равновесия и направив ось Оу по вертикали вниз, найти закон движения груза и период его колебаний, если в начальный момент времени длина пружины равна l₀=59,5см и грузу сообщена начальная скорость V₀=200см/с.

РЕШЕНИЕ.

1. В произвольный момент времени груз находится на расстоянии у от положения статического равновесия, принятого за начало координат. На груз действует сила тяжести и сила упругости пружины. В положении статического равновесия. (1)

2. Составим дифференциальное уравнение движения груза в проекции на ось у: (2)

или . (3)

Тогда с учетом (1) уравнение (3) примет вид . (4)

Разделим обе части уравнения на m и введем обозначение . Тогда получим. (5)

Решение дифференциального уравнения (5) выразим в виде y=C₁coskt+C₂sinkt. (6)

Постоянные интегрирования С₁ и С₂ определяем из начальных условий, предварительно продифференцировав по времени уравнение (6):

. (7)

При t=0 у=у₀ из уравнения (6): у₀=С₁;

из уравнения (7): V₀=kС₂; .

Из (рис. 15) видно, что ;

см; у₀=-[(60+39,2)-59,2]=--40см;

; С₁=у₀= -40;

Уравнение движения груза имеет вид у=-40cos5t+40sin5t.

Период колебания груза