18. Общее уравнение динамаики.

Принцип возможных перемещений дает общий метод решения задач статики. Принцип Даламбера использует методы статики для решения задач динамики. Применяя два эти принципа одновременно, можно получить общий метод решения задач динамики.

При движении механической системы с идеальными связями сумма элементарных работ заданных сил и сил инерции на любом возможном перемещении системы равна нулю (18.1) или. (18.2)

Рисунок 60

При наличии сил трения их нужно причислить к задаваемым силам. С помощью общего уравнения динамики можно определять силы по заданному движению (прямая задача динамики) или определять движение по заданным силам (обратная задача динамики). Для решения задач с помощью общего уравнения динамики необходимо:

1. показать на схеме активные силы и реакции неидеальных связей (например, силы трения);

2. добавить к активным силам силы инерции;

3. дать возможное перемещение точкам системы, выражая перемещение всех точек через возможное перемещение одной из точек системы;

4. составить общее уравнение динамики, вычисляя сумму элементарных работ всех активных сил и сил инерции на возможном перемещении точки их приложения;

5. решить полученное уравнение в соответствии с условием задачи

ПРИМЕР 26.

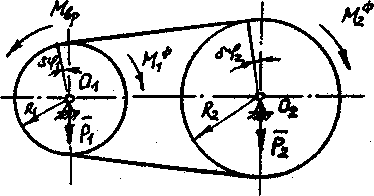
К шкиву 1 ременной передачи (рис. 61) приложен вращающий момент М_вр=3Нм. Массы шкивов равномерно распределены по их ободам и соответственно равны m₁=1кг и m₂=2кг. Радиус шкива 1 R₁=0,1м. Пренебрегая трением, определить угловое ускорение шкива 1.

Рисунок 61

РЕШЕНИЕ.

1. Массы шкивов равномерно распределены по их ободам и пропорциональны размерам:

;(1)

,

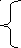
где -- плотность материала шкивов. Используя выражение (1), можно определить размер второго шкива

; м.

2. Силы инерции точек шкивов приводятся к моментам сил инерции, которые соответственно равны ; (2)

. (3)

Угловые ускорения колес обратно пропорциональны их радиусам, т.е.

или . Тогда. (4)

3. Запишем общее уравнение динамики . (5) Дадим системе возможное перемещение: шкив 1 повернется на угол, шкив 2—на угол. Вычислим работу активных сил и сил инерции на возможном перемещении системы. (6) Выразим возможное перемещениешкива 2 через:. Тогда, с учетом (2) и (4), получим:. (7) Так как, приравниваем нулю выражение, из которого находим угловое ускорение шкива 1:с^-2.

ПРИМЕР 27.

Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3, 4 и 5, прикрепленных к этим нитям, и невесомого блока 2. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М=12Нм., приложенных к шкиву 1. Радиусы ступеней шкива равны: R₁=0,2м, r₁=0,1м, а шкива 2—R₂=0,3м и r₂=0,15м;радиус инерции шкива 1 относительно оси вращения =0,1м (рис. 62). Пренебрегая трением, определить ускорение груза 3, если Р₁=30Н, Р₃=40Н, Р₄=20Н, Р₅=10Н.

РЕШЕНИЕ.

1. Рассмотрим движение механической системы, состоящей из тел 1, 2, 3, 4, 5, соединенных нитями. Система имеет одну степень свободы. Связи, наложенные на тела системы, относятся к идеальным. Для определения ускорения груза 3 применим общее уравнение динамики:

Рисунок 62

, (1) где -- сумма элементарных работ активных сил;

-- сумма элементарных работ сил инерции.

2. Покажем активные силы: ,,,и пару сил с моментом М. Зададим направление ускорения груза 3 и покажем силы инерции,,и момент сил инерции:;

;

; (2)

.

3. Дадим системе возможное перемещение и составим уравнение (1). . Выразим все перемещения через:;

;

; (3)

. С учетом выражений (2) и (3) уравнение (1) примет вид: (4) или. (5)

Выразим ,,через искомое ускорение груза:

; ;. (6) Так как, с учетом (6) приравниваем нулю выражение (5):. Откуда определим ускорениегруза 3:.