
Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002)
.pdf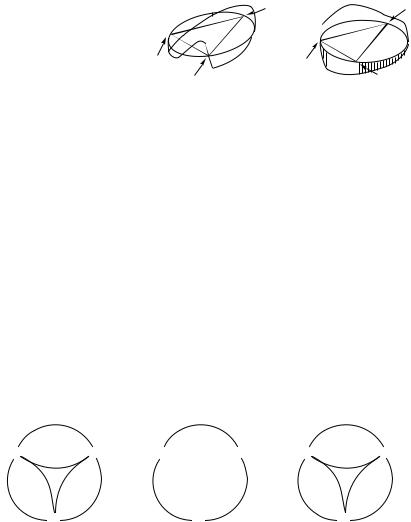
454 |
yehuda haas and shmuel zilberg |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
An i3 loop |
|
|
An ip2 loop |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ > 0 |
|
|
|
|
|
|
|
|
φ > 0 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
C |
Figure 10. A cartoon showing |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C-A |
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
the phase change in loops contain- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ < 0 |
|
|
|
|
|
|
|
|
|
|
B |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
ing a conical intersection. |
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ < 0 |
|||||||
The two coordinates that define the ‘‘plane’’ in which the loop located were discussed in Section II. In loops that encircle a conical intersection, there is always at least one phase-inverting reaction—we can choose its coordinate as the phase-inverting one. Let us assume that this is the reaction connecting A and B. The phase changes near the transition state lying along this coordinate. It must therefore be positive close to that locality. The electronic wave function of C, the third anchor is obtained from the in-phase combination of jAi and jBi, as shown in Section I. Therefore, there is always a phase-preserving coordinate connecting C and the vicinity of the TS between A and B. We shall make use of this property in the practical application of the method.
A given pair of anchors may be part of several loops, containing different conical intersections. A systematic search for the third anchor is conducted by considering the electrons that are to be re-paired (i.e., that form the chemical bonds that are created in the reaction). A pragmatic and systematic way of doing this is by considering first the re-pairing of the smallest possible number of
i |
|
|
p |
|
p |
A |
B |
A |
B |
A |
B |
Cl |
|
|
no Cl |
|
Cl |
(i)p |
(i)p |
(i)p |
(i)p |
(i)p |
(p)i |
C |
|
|
C |
|
C |
i x p x p = i |
|
|
p x p x p = p |
|
p x p x i = i |
i x i x i = i |
|
|
i x i x p = p |
|
p x i x p = i |
(a) |
|
|
(b) |
|
(c) |
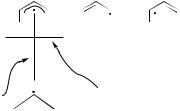
Figure 11. Three typical loops for the case where A is the reactant and B—the desired product. Loops in which a conical intersection may be found are (a) and (c). A loop that does not encircle a conical intersection is (b). In loop (a) the A ! B reaction is phase inverting, and in loops (b) and (c) it is phase preserving.
conical intersections in molecular photochemistry |
455 |
||||
Resonance stabilized out-of-phase combination |
|
||||
|
|
2 |
2 |
|
|
A |
|
1 |
3 − 1 |
3 |
|
|
A |
A |
|
|
|
|
|
{12,3} |
{1,23} |
|
|
Phase preserving coordinate |
2 |
Phase inverting coordinate |
|
||
|
|
|
|
||
1  3
3
A
{13,2}
Figure 12. The allyl/cyclopropyl radical loop.
electrons that change their pairing under the energy constraints of the reaction. In closed shell systems, at least four electrons must be involved since at least one phase inverting reaction is required. Next, reactions involving six electrons are considered, and so on.
A.Three-Electron Systems
We begin by considering a three-atom system, the allyl radical. A two anchor loop applies in this case as illustrated in Figure 12: The phase change takes place at the allyl anchor, and the phase-inverting coordinate is the asymmetric stretch C3 mode of the allyl radical. Quantum chemical calculations confirm this qualitative view [24,56]. In this particular case only one photochemical product is expected.
The allyl radical plays an important role in many photochemical transformations, as further discussed in Section IV.
B.Four-Electron Systems
Here the prototype is H4—as only three spin-pairing arrangements are possible, this system is simple to analyze. It turns out to be very frequently encountered in practice, even in rather complex systems.
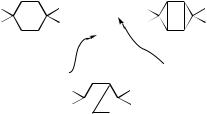
1.Four p Electrons: Butadiene Ring Closure
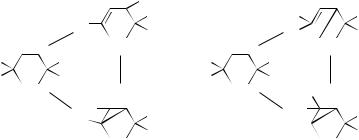
The classic example is the butadiene system, which can rearrange photochemically to either cyclobutene or bicyclobutane. The spin pairing diagrams are shown in Figure 13. The stereochemical properties of this reaction were discussed in Section III (see Fig. 8). A related reaction is the addition of two ethylene derivatives to form cyclobutanes. In this system, there are also three possible spin pairing options.


|
conical intersections in molecular photochemistry |
459 |
|||||||||||||
H/allyl conical intersection loop |
vinyl/allyl conical intersection loop |
||||||||||||||
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
||
|
|
|
* |
|
* |
|
|
|
* |
|
|
|
* |
||
|
|
i |
|
|
|
* |
|
|
i |
* |
|
|
|
* |
|
* |
|
* |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
||||||||||||
|
|
|
|
|
i |
* |
|
|
* |
|
|
i |
|
||
|
|
|
|
|
|
|
|||||||||
* |
|
|
* |
|
|
|
* |
|
|
* |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
i |
* |
* |
* |
|
|
i |
* |
|
|
|
* |
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
BCE(I) |
|
|
|
BCE(II) |
|
|||||
Figure 18. H/allyl (left) and vinyl/allyl (right) loops for CHDN.
to form bicyclo-[3,1,0]hex-2-ene [BCE(I)], and in the other to carbon atom 3, to form 1,3-cyclohexadiene (1,3-CHDN). In case the two electrons originate from a C–C single bond, one product is again BCE, but using isotopic labeling, it is clear that it is different from the molecule formed upon hydrogen migration. It is therefore labeled as BCE(II). The second product is vinylcyclobutene. As seen from Figure 18, both loops are phase inverting (i3 type), and enclose conical intersection. When a CH bond is cleaved, an H/allyl conical intersection is obtained and when a C–C bond is involved, a vinyl/allyl conical intersection. Both were reported in [65]. We designate the BCE isotopomer formed from the H/allyl loop as BCE(I). Both products of the loop encircling the vinyl/allyl CI were not observed experimentally. One of them, BCE(II), is the isotopomer expected from the di-p methane rearrangement [66].
The exchange of two pairs of s electrons is expected to lead to a high-lying conical intersection that is not likely to be important in the UV photochemistry of CHDN. This winds up the possibilities of loops involving two-electron pair exchanges only.
D.More Than Four Electrons
The next simplest loop would contain at least one reaction in which three electron pairs are re-paired. Inspection of the possible combinations of two fourelectron reactions and one six-electron reaction starting with CHDN reveals that they all lead to phase preserving i2p loops that do not contain a conical intersection. It is therefore necessary to examine loops in which one leg results in a two electron-pair exchange, and the other two legs involve three electron-pair exchanges (ip2 loops). As will be discussed in Section VI, all reported products (except the ‘‘helicopter-type’’ elimination of H2) can be understood on the basis of four-electron loops. We therefore proceed to discuss the unique helicopter
460 |
|
|
|
|
yehuda haas and shmuel zilberg |
|
|
|
|
||||||||||||||||||||
(a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b) |
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
* |
|
|
* |
||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
* |
||||||||
8 |
|
2 |
|
3 p |
8 |
|
3 |
|
|
|
8 |
|
|
3 |
|
|
|
|
i |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CHDN(I) |
|
|
|
|
|
|
|
CHDN(II) |
7 |
|
5 |
|
4 |
|
7 |
|
4 |
|
|
|
7 |
|
|
4 |
|
|
|
|
|
|
|
|
|
* |
||||
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
* |
|
|
|
|
|
|
||||||||
6 |
|
|
|
|
|
{23,45,78,16} |
|
|
|
* |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
{12,34,56,78} |
|
{82,34,57,16} |
|
{12,34,56,78} |
|
|
{13,45,67,82} |
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
* |
* |
|
|
* |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
(c) |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
* |
* |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
||||||||||||
*
pp
H2*
*
Figure 19. The proposed phase-inverting loop for the helicopter-type elimination of H2 off CHDN. The asterisks denote the H atoms that were originally bonded in the 1,4 positions of CHDN. Parts (a) and are (b) the anchors and (c) is the loop.
reaction, in which the H2 molecule departs from the carbon ring in a helicopter type motion [61,62].
The concerted CHDN ! benzene þ H2 reaction (Fig. 19a) has an aromatic transition state [67,68] and is thermally allowed (phase preserving). Three electron pairs are re-paired in the reaction. In order to construct a conical intersection containing Longuet-Higgins loop that has this reaction as one of the legs, we must look for another reaction of CHDN (or benzene þ H2) that is phase inverting. The reaction must involve the two hydrogen atoms (that are eliminated in the benzene-forming reaction), so that all four electrons of the two CH bonds must participate in the reaction. Obviously, other bonds must also change, so that in order for the reaction to be phase inverting, at least two more electron pair exchanges are required. Thus the simplest loop that contains a CI and leads to benzene and H2 in a concerted reaction is of ip2 type, in which the phase-inverting leg involves eight electrons. A reaction that suggests itself is the isomerization CHDN(I) ! CHDN(II), in which a shift of the two double bonds takes place, along with the associated transposition of hydrogen-atom bonds (Fig. 19b). Being a thermally ‘‘forbidden’’ reaction, it is likely to have a high barrier. The loop encircling the conical intersection that is defined by these three reactions is shown in Fig. 19c. The loops described in this section are the basis for the computation procedure detailed in Section VI.

462 |
yehuda haas and shmuel zilberg |
a crossing point between an excited and the ground state, that is, a conical intersection. In that sense, a Jahn–Teller system may be viewed as a special case of the more general problem of electronic degeneracy. In fact, by the Longuet– Higgins theorem, any degeneracy that connects the ground-state potential and the excited-state one, must be surrounded by a Longuet-Higgins loop, which can be formed by proper spin-paired combinations.
There is no analytic proof of the Jahn–Teller theorem. It was shown to be valid by considering all possible point groups one by one. The theorem is traditionally treated within perturbation theory: The Hamiltonian is divided into three parts
H ¼ HðrÞ þ HðRÞ þ Vðr; RÞ |
ð16Þ |
where HðrÞ is the pure electronic part, HðRÞ is the nuclear kinetic energy, and Vðr; RÞ is the electron–nuclear interaction. The parameter Vðr; RÞ is expanded with respect to small nuclear displacement from the initial configuration R0:
XX
Vðr; RÞ ¼ Vðr; R0Þ þ |
ðqV=qQaÞQa þ 1=2 ðq2V=qQaqQbÞQa Qb þ |
a |
a;b |
|
ð17Þ |
The terms PaðqV=qQaÞQa and 1=2 Pa;bðq2V=qQaQbÞQaQb are the linear and quadratic vibronic coupling terms, respectively. For small Qa values, they may
be considered as a perturbation.
If the solution of the zero-order Schro¨dinger equation [i.e., all terms in (17) except Vðr; R0Þ are neglected] yields an f-fold degenerate electronic term, the degeneracy may be removed by the vibronic coupling terms. If j i and j 0i are
the two degenerate wave functions, then the vibronic coupling constant |
|
FQa ¼ h ðqV=qQaj 0i |
ð18Þ |
is nonzero for some coordinate Qa (this is ensured by the lack of extremum at this point).
An example that is closely related to organic photochemistry is the E E case [70]. A doubly degenerate E term is the ground or excited state of any polyatomic system that has at least one axis of symmetry of not less than third order. It may be shown [70] that if the quadratic term in Eq. (17) is neglected, the potential surface becomes a moat around the degeneracy, sometimes called ‘‘Mexican hat.’’ The polar coordinates r and f, shown in Figure 20, can be used to write an expression for the energy:
E ðr; fÞ ¼ 1=2KEr2 r½FE2 þ GE2 r2 þ 2FEGEr cos 3f&1=2 |
ð19Þ |
FE and GE are the linear and coupling quadratic terms, respectively.
conical intersections in molecular photochemistry |
463 |
If the quadratic coupling cannot be neglected, the potential surface acquires three minima at f ¼ 0, 2p=3 and 4p=3. The two wave functions corresponding to the two branches are
¼ cosð =2Þjyi sinð =2ÞjEi |
ð20Þ |
þ ¼ sinð =2Þjyi þ cosð =2ÞjEi |
ð21Þ |
where jyi and jEi are the two electronic wave functions that are degenerate at r ¼ 0. tan y ¼ ðFE sin f jGEjr sin 2fÞ=FE cos f þ jGEjr cos 2fÞ.
When GE ¼ 0, it turns out that the two wave functions [Eqs. (20) and (21)] are not single valued: They change their sign when moving in a complete circle at the bottom of the moat! Since the total wave function must be single valued, this means that the electronic wave function must be multiplied by a phase factor eimf, with half-integer values of m. The energy is a function of m2, so that all levels are doubly degenerate, including the ground state.
It follows that the Jahn–Teller effect is a special case of the Longuet-Higgins rule, for systems of high nuclear symmetry. The degeneracy is removed as one moves away from the highly symmetric structure. The symmetry of the two electronic states that are formed for a given distortion may be determined from the symmetry of the problem, and was worked out for all point groups. The distortion in the Jahn–Teller problem are usually expressed in terms of the normal coordinates of the (fictitious) highly symmetric molecule that would have existed if a distortion did not take place.
In the more general case of nonsymmetric systems, we have shown that one can use reaction coordinates connecting two different spin-paired anchors. These two approaches should be equivalent; We shall show that this is indeed the case by discussing some examples.
Herzberg and Longuet-Higgins used the special case of the H3 system to demonstrate the relation of the Jahn–Teller theorem to the Longuet-Higgins loop [12]. We repeated their arguments in Section II (Figs. 4 and 5). LonguetHiggins went on to show, that the fact that three minima are obtained is not related to the C3v symmetry of the problem—the rule works for an arbitrary ABC system [13]. According to VB theory, any three-atom system for which the wave function of the transition state on the ground state is an out-of-phase combination of the wave functions of the reactant and products behaves in the same way. As we have seen (Sections I and III), this arises from a more fundamental symmetry property of the system: the permutational symmetry of the polyelectronic wave function and Pauli’s principle.
Accepting the Longuet-Higgins rule as the basis for the search of conical intersection, it is necessary to look for the appropriate loop. The E-type degeneracy of a Jahn–Teller system is removed by a nonsymmetric motion,

 {12,34}
{12,34} 3
3

 *
*