
- •Кубанский государственный аграрный университет
- •1.1.2. Изобразите геометрически множество истинности одноместных предикатов g(X) и p(X), если:
- •1.1.3. Изобразите геометрически множество истинности предиката p(X), решив систему неравенств:
- •1.1.4. Постройте матрицу двуместного предиката p(X,y) и проверьте решение геометрически:
- •1.1.5. Изобразите геометрически множество истинности двуместного предиката a(X, y).
- •1.1.6. Изобразите геометрически множество истинности двуместного предиката q(X,y).
- •1.2. Операции над предикатами и кванторами
- •1. Пусть предикат q(X,y) определен на конечных множествах:
- •1.3. Виды форм логики предикатов
- •1. Приведите формулу логики предикатов к приведенной форме:
- •2. Приведите формулу логики предикатов к приведенной форме, где X,y,z– вещественные переменные, применив отрицание к формуле:
- •3. Приведите формулу логики предикатов к предваренной нормальной форме XyP(X, y) XyQ(X, y).
- •1.3.1. Приведите формулу логики предикатов к приведенной нормальной форме:
- •1.3.2. Приведите формулы логики предикатов к приведенной нормальной форме, где X,y,z– вещественные переменны, применив отрицание к формуле:
- •1.3.3. Приведите к предваренной нормальной форме следующие формулы логики предикатов:
- •1.4. Применение логики предикатов
- •1.4.1. Запишите аксиомы положительных величин на языке логики предикатов, используя ограниченные кванторы:
- •9)Аксиома соизмеримости отрезков
- •1.4.2. Запишите некоторые аксиомы действительных чисел на языке логики предикатов, используя ограниченные кванторы:
- •1.4.3. Подберите элементарные предикаты и запишите следующие высказывания:
- •1.4.4. Запишите определения на языке логики предикатов, используя ограниченные кванторы, и постройте их отрицания:
- •1.4.5. Запишите определения на языке логики предикатов, используя ограниченные кванторы, и постройте их отрицания:
- •1.4.6. Запишите теоремы и свойства на языке логики предикатов, используя ограниченные кванторы, и постройте их отрицания:
- •0) Основная теорема алгебры.
- •1.4.7. Запишите теоремы на языке логики предикатов, используя ограниченные кванторы, и постройте их отрицания:
- •Глава 2. Комбинаторика
- •2.2. Размещения без повторений
- •2.3. Размещения с повторениями
- •2.4. Перестановки без повторений
- •2.5. Перестановки с повторениями
- •2.6. Инверсии. Обратные перестановки
- •2.7. Сочетания без повторений
- •2.8. Сочетания с повторениями
- •2.9. Примеры решения сложных задач
- •2.10. Треугольник Паскаля. Бином Ньютона
- •1. Запишите разложение бинома:
- •2. Вычислите без калькулятора:
- •3. Запишите разложение бинома:
- •Зачетные задания по теме «Комбинаторика»
- •Глава 3. Графы
- •3.1. Виды графов. Изоморфизм графов.
- •Основные положения о вершинах графа:
- •Алгоритм распознавания изоморфизма двух графов g1(X, e)и g2(y,e)
- •2. Докажите, что графы g1(x1, e1) и g2(y2, e2) изоморфны.
- •3. Решите задачу по вычислению валентности вершин графа
- •4. Решите задачу по выявлению связности компонент графа
- •3.1.5. Определите виды графов и подсчитайте валентность вершин:
- •3.1.6. Определите виды графов и подсчитайте валентность вершин:
- •3.1.7. Решите задачи по вычислению валентности вершин графа:
- •3.1.8. Решите задачи по вычислению валентности вершин графа:
- •3.1.9. Решите задачи по выявлению связности графа:
- •3.2. Операции над графами
- •3.2.1. Пусть заданы два графа g1(v1, e1) и g2(v2, e2). Изобразите геометрически объединение, пересечение и сумму по модулю два.
- •3.3. Представление графов в пэвм
- •3.3.1. Неориентированные графы
- •Способы задания графа:
- •Свойства матрицы смежности:
- •Свойства матрицы инцидентности:
- •2. Граф g(V,e): задан геометрически.
- •3. Графы g1(v1,e1) и g2(v2,e2) заданы геометрически.
- •3.3.1.2. Постройте для графа g(V,e), заданного геометрически
- •3.3.1.3. Дана матрица смежности графа. Задайте граф геометрически. Укажите: 1) матрицу инцидентности; 2) валентность вершин. 7)
- •Свойства матрицы инцидентности:
- •1. Орграф g1(V,e) задан геометрически. Постройте для орграфа:
- •2. Решите следующую задачу по обходу графов:
- •3.3.2.2. Орграф задан геометрически. Укажите валентность вершин. Постройте матрицу смежности орграфа.
- •3.3.2.3. Дана матрица смежности орграфа. А) Задайте орграф геометрически, в) постройте матрицу инцидентности.
- •3.3.2.4. Дана матрица инцидентности орграфа. А) Задайте орграф геометрически, в) постройте матрицу смежности.
- •3.3.2.5. Решите следующие задачи по обходу графов:
- •Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?
- •3.3.2.6. Решите следующие задачи по обходу графов:
- •3.4. Задачи оптимизации на графах
- •3. Задайте граф геометрически и решите задачу:
- •3.5. Эйлеровы и гамильтоновы графы
- •Критерий эйлеровости графа
- •1. Каждое ребро полного графа с 11 вершинами покрашено в один из двух цветов: красный или синий. Докажите, что либо "красный", либо "синий" граф не является плоским. 7)
- •3.5.3. Граф задан геометрически. Выпишите гамильтонов цикл у данного графа, если он есть:
- •Глава 4. Автоматы
- •4.1. Задачи анализа автоматов
- •4.2. Задачи синтеза автоматов
- •Глава 5. Алгоритмы
- •5.1.1. Опишите алгоритмы в словесной форме:
- •5.1.2. Опишите алгоритмы в словесно-формульной форме:
- •5.2. Виды алгоритмов
- •5.2.1. Линейные алгоритмы
- •1. Опишите графическим способом алгоритм расчета нормы расхода гербицида (л/га) по формуле:.
- •1. Опишите алгоритмы в графической форме, в которых переменной d присваивают:
- •2. Опишите алгоритмы в графической форме. Даны положительные вещественные числа X и y. Присвойте целой переменной z:
- •5.2.2. Разветвляющиеся алгоритмы
- •1. Опишите графическим способом алгоритм вычисления значения выражения:
- •4. Даны действительные числа X, y и z. Вычислите:
- •5.2.3. Циклические алгоритмы
- •Выход из цикла Выход из цикла
- •1.Составьте блок-схему алгоритма вычисления среднеквадратической взвешенной по формуле:
- •2.Составьте блок-схему алгоритма вычисления суммы кубов последовательности, состоящей из положительных чисел до первого введенного отрицательного числа.
- •5.3. Применение теории алгоритмов. Машины Тьюринга
- •1. Пусть требуется добавить 1 к натуральному числу n, представленному на ленте машины Тьюринга в двоичной системе счисления, то есть в алфавите {0,1}.
- •3. Составьте программу машины Тьюринга, подсчитывающую число вхождений символа a в слово р в алфавите {a, b, c}.
- •5.3.1. Постройте машину Тьюринга,
- •5.3.2. Постройте машину Тьюринга, подсчитывающую
- •5.3.3. Постройте машину Тьюринга, осуществляющую перевод натурального числа n
- •5.3.4. Постройте машину Тьюринга,
1. Запишите разложение бинома:
|
|
|
|
|
|
|
|
|
|
2. Вычислите без калькулятора:
|
|
|
|
|
|
|
|
|
|
3. Запишите разложение бинома:
|
|
|
|
|
|
|
|
|
|
Зачетные задания по теме «Комбинаторика»
Задание 1.
Из города А в город В ведут пять дорог, а из города В в город С – три дороги. Сколько путей, проходящих через В, ведут из А в С?
Из двух спортивных обществ, насчитывающих по 100 фехтовальщиков каждое, надо выделить по одному фехтовальщику для участия в состязании. Сколькими способами может быть сделан этот выбор?
Имеется пять видов конвертов без марок и четыре вида марок одного достоинства. Сколькими способами можно выбрать конверт с маркой для посылки письма?
Сколькими способами можно выбрать гласную и согласную буквы из слова «камзол»?
Сколькими способами можно выбрать гласную и согласную буквы из слова «здание»?
Бросают игральную кость с шестью гранями и запускают волчок, имеющий восемь граней. Сколькими различными способами они могут упасть?
На вершину горы ведут пять дорог. Сколькими способами •турист может подняться на гору и спуститься с нее? То же самое при условии, что спуск и подъем происходят по разным путям.
На ферме есть 20 овец и 24 свиньи. Сколькими способами можно выбрать одну овцу и одну свинью? Если такой выбор уже сделан, сколькими способами можно сделать его еще раз?
Сколькими способами можно указать на шахматной доске два квадрата – белый и черный? А если нет ограничений на цвет выбранных квадратов?
Из 12 слов мужского рода, 9 женского и 10 среднего надо выбрать по одному слову каждого рода. Сколькими способами может быть сделан этот выбор?
Задание 2.
В местком избрано 9 человек. Из них надо выбрать председателя, заместителя председателя, секретаря и культорга. Сколькими способами это можно сделать?
Из состава конференции, на которой присутствует 52 человека, надо избрать делегацию, состоящую из 5 человек. Сколькими способами это можно сделать?
Автомобильные номера состоят из одной, двух или трех букв и четырех цифр. Найти число таких номеров, если используются 32 буквы русского алфавита.
Сколько различных перестановок можно получить, переставляя буквы в слове «математика»? В слове «парабола»?
В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нем 12 открыток? Сколькими способами можно купить 8 открыток?
Из группы, состоящей из 7 мужчин и 4 женщин, надо выбрать 6 человек так, чтобы среди них' было не менее 2 женщин. Сколькими способами это можно сделать?
Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены им отметки, если известно, что никто из них не получил неудовлетворительной отметки?
Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется хотя бы один туз?
Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется ровно один туз?
Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется ровно два туза?
|
Задание 3. Записать все размещения из элементов множества А по два элемента с повторениями:
|
Задание 4. Записать все размещения из элементов множества А по три элемента без повторений:
| |
|
Задание 5. Записать все сочетания из элементов множества А по два элемента без повторений:
|
Задание 6. Записать все сочетания из элементов множества А по три элемента с повторениями:
| |
|
Задание 7. Записать все перестановки без повторений из элементов множества А:
|
Задание 8. Записать все: - размещения из элементов множества А по три элемента с повторениями; - размещения из элементов множества А по четыре элемента без повторений; - сочетания из элементов множества А по четыре элемента без повторений; - сочетания из элементов множества А по три элемента с повторениями; - перестановки из элементов множества А без повторений; 0) А = {1,3,5,7,8}; 1) А= {2,a,1,d,8}; 2) A = x,y,z,t,1; 3) A = a,b,z,t,2}; 4) A= {a,b,d,1,2}; 5) A = {a, b, c, d,х}; 6) A= {a,b,d,e,f}; 7) A = {x, y, a, b,6}; 8) A ={х,с,3,8,0}; 9) A = {с, b, 3, d, 4}. | |
|
Задание 9. Сколько трехзначных чисел, меньших заданного числа А, можно образовать, используя цифры 2,3,4,5,6,8,9 без повторений, если: 0) А=450; 1) А=350; 2) А=250; 3) А=420; 4) А=410; 5) А=380; 6) А=370; 7) А=430; 8) А=390; 9) А=460. |
Задание 10. Сколькими способами N пар, пришедших в кино, могут занять места, если все пять пар сидят подряд и:
0) N=4; 1) N=5; 2) N=7; 3) N=6; 4) N=8; 5) N=9; 6) N=3; 7) N=10; 8) N=12; 9) N=11. | |
|
Задание 11. В соревнованиях участвуют N спортсменов. Сколько существует вариантов распределения трех призовых мест, если: 0) N=8; 1) N=7; 2) N=6; 3) N=9; 4) N=10; 5) N=5; 6) N=11; 7) N=12; 8) N=15; 9) N=14. |
Задание 12. Сколько существует N-битовых строк, содержащих А нулей и К единиц, если: 0) N=8; А=3, К=5; 1) N=8; А=2,К=6; 2) N=8; А=4, К=4; 3) N=9; А=2,К=7; 4) N=9; А=3, К=6; 5) N=9; А=4, К=5; 6) N=10; А=3, К=7; 7) N=10; А=4, К=6; 8) N=10; А=2, К=8; 9) N=10; А=5, К=5. | |
|
Задание 13. В совете директоров компании, состоящего из n человек, при выборе президента за выдвинутую кандидатуру проголосовали k человек, против —j, воздержались — s. Сколькими способами может быть проведено такое голосование?
|
Задание 14. Сколькими способами из группы в n человек можно сформировать k групп по i человек, s групп по l человек и m групп из j человек, если:
| |

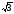 )4;
)4;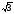 +3y) 4;
+3y) 4;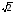 )4;
)4;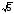 +2y) 4;
+2y) 4;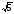 )4;
)4;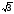 –
2y) 4;
–
2y) 4;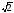 )4;
)4;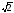 +4y) 4;
+4y) 4;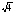 )4;
)4;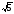 +3y) 4;
+3y) 4;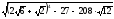 ;
;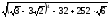 ;
;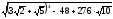 ;
;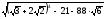 ;
;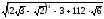 ;
;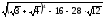 ;
;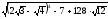 ;
;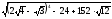 ;
;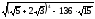 ;
;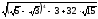 ;
;