2.7. Сочетания без повторений

Сочетаниями из n элементов по m (m n) называются неупорядоченные m-элементные выборки из данных n элементов.

Задания для самостоятельного выполнения

1. Составьте все сочетания из трех букв А, В, С по две буквы.

2. У 6 взрослых и 11 детей обнаружены признаки инфекционного заболевания. Чтобы проверить заболевание, следует взять выборочный анализ у 2 взрослых и 3 детей. Сколькими способами можно это сделать?

3. Сколькими способами можно группу из 20 студентов разделить на две подгруппы так, чтобы в одной группе было 13, а в другой 7 человек?

4. На книжной полке стоят 3 книги по алгебре, 4 книги по геометрии и 5 книг по литературе. Сколькими способами можно взять с полки три книги по математике?

5. Учащийся хочет использовать для раскраски географической контурной карты 4 краски из 6, которые он имеет в своем распоряжении. Сколькими способами он может выбрать 4 краски из 6?

6. Даны две параллельные прямые. На одной из них имеется 10 точек, а на другой - 20. Сколько существует треугольников с вершинами в данных точках?

7. Сколькими способами можно распределить 28 костей домино между 4 игроками так, чтобы каждый получил 7 костей?

8. В классе 12 юношей и 13 девушек. Сколькими способами из них можно выбрать четырех учащихся для дежурства на вечере, если а) освободить девушек; б) юноши и девушки?

9. Сколькими способами абитуриент может выбрать 3 ВУЗа из 5 для подачи документов?

10. Из двух математиков и десяти экономистов надо составить комиссию в составе восьми человек. Сколькими способами может быть составлена комиссия, если в нее должен входить хотя бы один математик?

2.8. Сочетания с повторениями

Сочетаниями с повторениями из n по m называются неупорядоченные m-элементные выборки, в которых элементы могут повторяться.

Задания для самостоятельного выполнения

1. В почтовом отделении имеются открытки 3 видов. Сколькими способами можно купить набор из 6 открыток?

2. Сколькими способами можно выбрать четыре из четырех пятикопеечных монет и из четырех двухкопеечных монет?

3. В хлебном отделе имеются булки белого и черного хлеба. Сколькими способами можно купить 8 булок хлеба?

4. Сколько имеется костей в обычной игре "домино"?

5. Сколько вариантов строения ДНК Шубуршунчика обворожительного может быть, если длина цепи 1000 нуклеотидов (нуклеотиды 4 видов: А, Т, Г, Ц)?

6. Сколько всего чисел можно составить из цифр 1, 2, 3, 4, 5, в каждом из которых цифры расположены в неубывающем порядке?

7. Шесть пассажиров садятся на остановке в трамвайный поезд, состоящий из трех трамвайных вагонов. Сколькими различными способами могут они распределиться в каждом из 3 вагонов?

8. Как велико число отличных друг от друга результатов бросаний двух одинаковых кубиков?

9. Сколькими способами можно выбрать 7 крупных апельсинов из 2 имеющихся на рынке сортов?

10. В магазине продаются белые, черные и красные носки. Сколькими способами можно купить 5 пар?

2.9. Примеры решения сложных задач

Приведем в систему полученные формулы всех 6 видов комбинаций с повторениями и без повторений, представив алгоритм определения вида комбинации (см. рис. 1).

Задания для самостоятельного выполнения

1. Из 10 роз и 8 георгинов нужно составить букет так, чтобы в нем было 2 розы и 3 георгина. Сколькими способами это можно сделать?

2. Собрание из 40 человек избирает председателя, секретаря и трех членов редакционной комиссии. Сколько существует возможностей выбора этих пяти человек?

3. Сколькими способами можно расставить 8 томов энциклопедии на книжной полке так, чтобы первый и второй тома:

а) стояли рядом; б) не стояли рядом?

4. На окружности расположено 20 точек. Сколько существует вписанных треугольников с вершинами в этих точках?

5. Сколько существует номерных знаков для автомобилей, состоящих из двух букв с последующими четырьмя цифрами, если буквы могут повторяться, а цифры — нет?

6. Лифт, в котором находится восемь пассажиров, останавливается на шести этажах. Пассажиры выходят группами по одному, три и четыре человека. Сколькими способами это может произойти, если на каждом этаже может выйти только одна группа пассажиров, при этом порядок выхода пассажиров одной группы не имеет значения?

7. В алфавите племени Бум-Бум шесть букв. Словом является любая последовательность из шести букв, в которой есть хотя бы две одинаковые буквы. Сколько слов в языке племени Бум-Бум?

8. В стране 20 городов, каждые два из которых соединены авиалинией. Сколько авиалиний в этой стране?

9. На глобусе проведены 17 параллелей и 24 меридиана. На сколько частей разделена поверхность глобуса? Меридиан — это дуга, соединяющая Северный полюс с Южным. Параллель — это окружность, параллельная экватору (экватор тоже является параллелью).

Указание. Решите задачу для двух меридианов (0^o и 180^o) и одной параллели (экватора).

10. У людоеда в подвале томятся 25 пленников.

а) Сколькими способами он может выбрать трех из них себе на завтрак, обед и ужин? б) Сколько есть способов выбрать 3-х, чтобы отпустить на свободу?

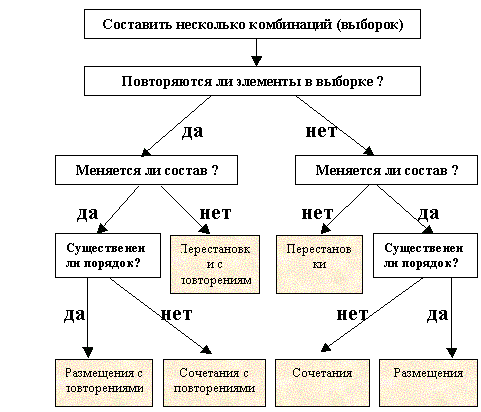
Рис. 1. Алгоритм определения вида комбинации