1.4.7. Запишите теоремы на языке логики предикатов, используя ограниченные кванторы, и постройте их отрицания:

1. Теорема Фейера о суммировании средними арифметическими.

Каждый ряд Фурье суммируем средними арифметическими к функции f(t) при всех t в интервале (-T/2, T/2), для которых функция f(t) непрерывна; в точках разрыва первого рода средние арифметические сходятся к (f(t – 0) + f(t + 0))/2

2. Теорема Вейерштрасса об изолированной особой точке.

Пусть f(z) – однозначная функция, имеющая изолированную особую точку при z = a. Тогда для любого комплексного числа А (включая А = ) существует последовательность точек z_k  a такая, что lim f(z_k) = A при k  .

3. Теорема Пикара об изолированной особой точке.

Пусть f(z) – однозначная функция, имеющая изолированную особую точку при z = a. Тогда для любого комплексного числа А  , за исключением, быть может, одного значения А = А₀ , каждая окрестность точки а содержит бесконечное множество точек z таких, что f(z) = A.

4. Теорема Лагранжа о конечном приращении.

Если функция f(x) непрерывна на [a, b] и дифференцируема на (a, b), то в интервале (a, b) существует такое число X, что f(b) – f(a) = f’(X)(b – a).

5. Теорема Вейерштрасса о приближении.

Пусть f(x) – действительная функция, непрерывная на ограниченном замкнутом интервале [a, b]. Тогда для каждого заданного положительного числа  существует такой действительный многочлен

P(x)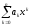 , чтоf(x) – P(x) < при всех x  [a, b].

6. Теорема Коши о среднем значении

Если функции u(x) и v(x) непрерывны на [a, b] и v(b)  v(a) и существуют производные u’(x) и v’(x) в интервале (a, b) и одновременно не обращаются в нуль, то в интервале (a, b) существует такое число X, что

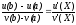
7. Теорема Руше о нулях функции

Если f₁(z) и f₂(z) – аналитические функции в ограниченной области D и на ее контуре C и если | f₂(z)| < | f₁(z)|  0 на С, то функции f₁(z) и f₁(z) + f₂(z) имеют одинаковое число нулей в области D.

8. Теорема о функциях, разложимых в ряд Фурье

Ряд Фурье или интеграл Фурье, порожденный действительной функцией f(t), абсолютная величина которой интегрируема на интервале разложения I, сходится равномерно к f(t) на каждом таком интервале (a, b)  (a - , b + )  I, где  > 0, что на (a - , b + ) функция f(t) непрерывна.

9. Теорема Фейера о cходимости средних арифметических.

Средние арифметические сходятся к f(t) почти всюду в интервале разложения; они сходятся к f(t) равномерно на каждом таком интервале (a, b)

10. Теорема Ролля об отделении действительных корней

Пусть a и b – два соседних действительных корня уравнения f’(x) = 0 и пусть f(a)  0 и f(b)  0. Уравнение f(x) = 0 между a и b либо вовсе не имеет действительных корней, либо имеет один действительный корень в зависимости от того, будут ли числа f(a) и f(b) иметь одинаковые или противоположные знаки.

Глава 2. Комбинаторика

1. Правила суммы и произведения

Правило суммы. Если объект А можно выбрать n способами, а объект В k способами, то объект "А или В" можно выбрать n+k способами. Правило произведения. Если объект А можно выбрать n способами, а объект В независимо от него k способами, то пару объектов "А и В" можно выбрать n · k способами.

Задания для самостоятельного выполнения

1. В ящике находятся 20 шаров: 5 белых, 6 черных, 7 синих и 2 красных. Сколькими способами можно взять из ящика один цветной шар?

2. В розыгрыше первенства по футболу принимают участие 18 команд. Сколькими способами могут быть распределены золотая, серебряная и бронзовая медали, если любая команда может получить только одну медаль?

3. При формировании экипажа космического корабля имеется 10 претендентов на пост командира экипажа, 20 - на пост бортинженера и 25 - на пост космонавта-исследователя. Ни один кандидат не претендует одновременно на два поста. Сколькими способами можно выбрать одну из кандидатур или командира, или бортинженера, или космонавта-исследователя?

4. Сколькими способами можно выбрать на шахматной доске белый и черный квадраты, не лежащие на одной и той же горизон­тали и вертикали?

5. Имеется 6 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну — на правую руку так, чтобы эти перчатки были различных размеров?

6. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?

7. В ящике лежат 4 черных и 3 белых шара. Наудачу вынимаются последовательно два шара. Какова вероятность того, что оба эти шара окажутся белыми? (Шар после выбора в ящик не возвращается.)

8. В столовой предлагают два различных первых блюда a₁и а₂, три различных вторых блюда b₁, b₂, b₃и два вида десерта с₁и c₂. Сколько различных обедов из трех блюд может предложить столовая?

9. У англичан принято давать детям несколько имен. Сколь­кими способами можно назвать ребенка, если общее число имен равно 300, а ему дают не более трех имен?

10. На вершину горы ведут пять дорог. Сколькими способами турист может подняться на гору и спуститься с нее? То же самое при условии, что спуск и подъем происходят по разным путям.