
may05119
.pdfФ е дерал ь ное агент с т во по образованию Гос ударс т ве нное образоват ел ь ное уч реж дение
выс ш е го профес с ионал ь ного образования «Воронеж с кийгос ударс т венныйуниверс ит ет » (ГО У ВП О ВГУ)
М А Т ЕМ А Т И К А
Уч ебное пос обие
по с пе циал ь нос т и: 030701 (350200) - М еж дународные от нош ения по направл е нию : 080200 (521300) - Регионоведе ние
Вороне ж
2005
2
Ут верж дено науч но-ме т одич ес ким с овет ом факул ьт ет а меж дународны х от нош е ний от 24.01.2005г., прот окол № 5.
Сос т авит ел ь |
пре подават е л ь кафедры |
|
«М е ж дународнойэкономики и |
|
внеш неэкономич ес койдеят ел ь - |
|
нос т и», кандидат т ехнич е с ких |
|
наукГайворонс кая С.А. |
Реце нзент |
Ст арш ийпреподават ел ь , кафедры |
|
М М И О факул ь т ет а П М М Воро- |
|
неж с кого гос ударс т ве нного уни- |
|
верс ит е т а, Б ондаре нко Ю .В. |
П ос обие подгот овл ено накафедре «М еж дународнойэкономики и вне ш не экономич е с койдеят е л ь нос т и» факул ь т ет аме ж дународныхот но- ш е нийВоронеж с кого гос ударс т ве нного универс ит ет а.
Уч ебное пос обие пре дназнач ено дл я с т удент ов факул ьт е т аме ж дународныхот нош е нийгуманит арныхс пе циал ь нос т е й.
В пос обии рас с мат риваю т с я ос новные понят ия и мет оды мат е мат и- ч ес кого анал иза, т еории множ ес т в, л инейной ал ге бры , мат емат ич е с кого модел ирования, т еории вероят нос т е йи мат емат ич е с койс т ат ис т ики.
П риводят с я т екс т ы л екций, примеры ре ш е ния задач , конт рол ь ны е вопрос ы и задания по рас с мот ренным т емам.
3
В мат емат ич ес ких предл ож е ниях (формул ировкахопредел ений, т еорем и т .д.) ч ас т о повт оряю т с я от дел ь ные с л оваи цел ы е выраж е ния. П о- эт ому при запис и ис пол ь зую т с имвол ы :
· $ - с ущ е с т вуе т (от англ ийс кого с л оваExistence - с ущ е с т вование )
·" - л ю бой(от англ ийс кого с л оваAny - л ю бой)
·: - т акой, ч т о
·Þ - выпол няет с я
Г л а в а 1. Э л ем енты теор ии м ножеств . Пр едел посл едов а тел ьности.
§1. М ножеств а . Опер а ции на дм ножеств а м и
П онят ие множ ес т ваявл яет с я одним из ос новны х в мат емат ике . О но
принадл е ж ит к первич ным, неопре дел яемы м понят иям. |
М ы т ол ько мож е м |
|||||||||||||||
привес т и примеры : множ е с т во с т уде нт ов в аудит ории, |
множ ес т во с т уден- |
|||||||||||||||
т ов, пол уч ивш ихнаэкзамене оце нку «пят ь», и т .д. |
|
|
|
|
|
|
|
|||||||||
|
|
О бъект ы, входящ ие в множ е с т во, будем называт ь э л ем ента м и м но - |
||||||||||||||
ж ес тва . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
М нож ес т ваобознач аю т с я бол ь ш ими буквами, аих эл е ме нт ы – ма- |
||||||||||||||
л е нь кими. |
Т акж е |
множ е с т ва обознач аю т с я кругами, |
их называю т |
круги |
||||||||||||
Э йлер-В ена . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Е с л и x явл яет с я эл емент ом множ ес т ва X , т о пиш ут x X , в прот ив- |
||||||||||||||
ном с л уч ае - |
x X . |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Е с л и |
|
31 ,...,2 xn, |
,x– x |
некот орые |
эл е ме нт ы, |
т о |
|
запис ь |
||||||
= { |
|
|
31 ,...2, xn,} |
,означx X x аеx т , |
ч т о |
множ е с т во |
X с ос т оит |
из эл емент ов |
||||||||
|
|
31 ,...,2 xn, . ,x |
x |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
П ус т ь |
X и Y – двамнож е с т ва. Ес л и |
X и Y с ос т оят из однихи т ехж е |
||||||||||||
эл емент ов, т о говорят , ч т о они с овпадаю т : |
X = Y . |
|
|
|
|
|
|
|
||||||||
|
|
Е с л и множ ес т во с одерж ит |
л иш ь коне ч ное ч ис л о эл еме нт ов, |
т о оно |
||||||||||||
называе т с я ко нечны м , в прот ивном с л уч ае множ е с т во – б ес ко нечно . |
|
|||||||||||||||
|
|
|
|
|
Способы за да ния м ножеств |
|
|
|
|
|
|
|
||||
1. П ереч ис л ение вс ехэл емент ов данного множ ес т ва: |
= { |
|
|
, d,}cA. b a |
||||||||||||
Н о не вс е гдаэл емент ы мож но переч ис л ит ь . |
|
|
|
|
|
|
|
|
||||||||
2. С помощ ь ю характ ерис т ич е с кого с войс т ва, |
кот оры м обл адаю т |
эл емен- |
||||||||||||||
т ы данного множ ес т ваи не обл адаю т эл емент ы другого множ ес т ва. |
|
|||||||||||||||
П ус т ь |
P (x) |
– какое-т о с войс т во ч ис л а x , |
т огда запис ь { |
|
|
(xx)}Pознач ае т |
||||||||||
|
||||||||||||||||
множ ес т во вс е хч ис ел , обл адаю щ ихс войс т вом |
P (x). |
|
|
|
|
|
|
|
||||||||
Пр им ер ы . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1. { |
|
2 |
x |
x−=3x0}+-2ес т ь с овокупнос т ь корне йуравне ния x2 |
x |
−=30 ,+т2.е. |
||||||||||
|
||||||||||||||||
эт о множ ес т во с ос т оит из двухэл е мент ов { |
21,}. |
|
|
|
|
|
|
|
|
|||||||
2. {x |
|
3 < x < 7} – |
4 |
|
множ е с т во вс ех ч ис ел , удовл ет воряю щ их нераве нс т ву |
||
|
|||
3 < x < 7 , т .е . x ( |
7,3). |
||
Пр им ер ы числ ов ы хм ножеств
1.N={1, 2, 3, … } – множ ес т во нат урал ь ныхч ис е л .
2.Z={NÈN_È 0} – множ е с т во це л ыхч ис ел .
3. |
Q={ m - нес ократ имы е, mÎZ, nÎN} – множ е с т во рационал ь ны хч ис ел . |
|
||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
R={-¥, +¥} – множ ес т во де йс т вит ел ь ныхч ис ел . |
|
|
|
|
|
|
|
|
|
||||
|
Опер а ции на дм ножеств а м и |
|
|
|
|
|
|
|
|
|
||||
1. |
О бъединение м ножеств . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
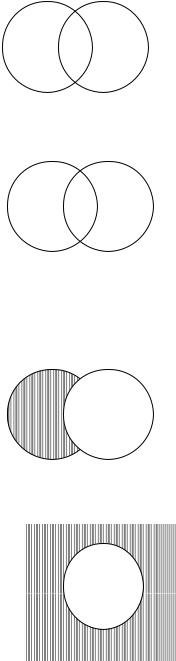
Об ъединением двух м но ж ес тв Х и Y назы - |
|
|
|
|
|
|
|
|
|
|
|
||
вает с я множ ес т во, с ос т оящ е е |
из |
эл еме нт ов, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
кот оры е принадл е ж ат множ ес т ву Х |
ил и мно- |
|
|
|
X |
|
|
|
Y |
|
|
|
||
ж е с т ву Y. О бознач ает с я Х ÈY. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Х ÈY = {x½ х Х ил и х Y }. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Пер есечение м ножеств . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
П ерес ечением двух м но ж ес тв Х и Y называ- |
|
|
|
|
|
|
|
|
|
|
|||
ет с я множ е с т во, с ос т оящ ее из эл еме нт ов, кот о- |
|
|
|
|
|
|
|
|
|
|
||||
ры е принадл е ж ат как множ ес т ву Х , т ак и мно- |
|
|
|
|
|
|
|
|
|
|
||||
|
|
X |
|
Z |
Y |
|
|
|||||||
ж е с т ву Y, т .е. их общ ая ч ас т ь . |
О бознач ает с я |
|
|
|
|
|
||||||||
Х ÇY, Х ÇY = {x½ х Х и х Y }, |
нарис унке пе- |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
рес еч ение множ ес т в Х и Y – множ ес т во Z. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М нож ес т ва, кот орые не име ю т общ ихэл еме нт ов, называю т с я непе-
рес ека ю щим ис я.
3. Ра зностьм ножеств . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Разнос т ью |
множ ес т в Х |
и Y |
называе т с я |
|
|
|
|
|
|
|
|
|
||
множ ес т во, с ос т оящ ее из вс ех эл е мент ов мно- |
|
|
|
|
|
|
|
|
|
|||||
ж е с т ваХ , не принадл еж ащ ихмнож ес т ву Y. |
|
X |
|
Y |
|
|
||||||||
О бознач ает с я Х \Y = {х½хÎХ и хÏY}, |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
(нарис унке разнос т ь множ е с т в заш т рихована) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
Допол нение м ножеств |
|
|
|
|
|
|
|
|
|||||
М нож ес т во вс ех эл емент ов |
Х , не |
принадл е ж ащ их |
|
|
|
|
|
|
|
|
||||
множ ес т ву Y, явл яе т с я до по лнением |
множ е с т ваY до |
|
|
|
|
|
|
|
|
|||||
множ ес т ва Х . |
О бознач ает с я |
|
Х , |
(на рис унке за- |
|
|
|
|
|
|
|
|
||
Y |
|
|
|
|
|
|
|
|
||||||
|
|
|
X |
|
|
|
||||||||
ш т рихованная |
ч ас т ь ). Н апример, множ е с т во цел ых |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
непол ож ит е л ь ных ч ис е л ес т ь |
допол не ние множ ес т ва |
|
|
Х |
|
|
|
|
|
|||||
Y |
|
|
|
|
|
|||||||||
N нат урал ь ны хч ис ел до множ е с т вацел ы хч ис е л . |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5
§2. Пр им ер ы р еш ения за да ч на тем у «Э л ем енты теор ии м ножеств »
Ра ссм отр им способы за да ния м ножеств :
1. Д ано множ ес т во {x 2x + 5 = 2(x + 5)}. Ч е му оно равно?
П ерепиш ем раве нс т во 2x + 5 = 2x +10 . П роводя преобразования, пол уч им: 0 = 5 . Ч т о не возмож но, поэт ому {x 2x + 5 = 2(x + 5)} = Æ .
2. {x 2(3x + 7) = 6x +14}
П ерепиш ем раве нс т во6x +14 = 6x +14 , т .е. раве нс т во ве рно при л ю бом зна-
ч ении x , т огда{ |
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
) |
|
} { |
|
x x( |
,+¥)x}.¥x- Î x 14= ++6 =7 2 3 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
П роводя анал огич ные рас с уж дения мож но ре ш ит ь с л едую щ ие задач и: |
|||||||||||||||||||||||||||||||||||||||
3. |
{ |
|
|
|
|
|
|
} { |
|
x x[0, x¥x)+}x Î= = |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
4. |
{ |
|
|
|
|
|
|
|
} { |
|
|
|
|
|
|
|
|
|
|
|
|
|
x Z[ , x2 ¥x )+}, |
Îx ,ZxÎx2Î = ³ |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
В примерах5-8 необходимо рас с мот ре т ь корни уравнения, ими явл яю т - |
||||||||||||||||||||||||||||||||||||||
с я ч ис л а- 1, 1 , ± |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì |
|
|
|
|
|
|
|
æ |
|
|
|
|
|
1 ö |
|
|
2 |
ü |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
5. |
íx |
x Î N, |
(x +1)ç x - |
|
|
|
|
|
|
÷ |
(x |
|
- 2) = 0ý |
= Æ |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
î |
|
|
|
|
|
|
|
è |
|
|
|
|
|
2 ø |
|
|
|
þ |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
ì |
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
|
1 ö |
|
2 |
ü |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
6. |
íx |
x Î Z, |
(x +1)ç x |
- |
|
|
|
|
÷ |
(x |
|
|
- 2) = 0ý |
= {-1} |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
î |
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
2 ø |
|
|
|
þ |
|
|
|
|
|
|
|
|
|
|
||||||||
|
ì |
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
|
1 ö |
|
2 |
ü |
ì |
|
|
|
1 |
ü |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
7. |
íx |
x ÎQ, |
(x +1)ç x |
- |
|
|
|
|
÷ |
(x |
|
|
- 2) = 0ý |
= í-1, |
|
|
ý |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
î |
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
2 ø |
|
|
|
þ |
î |
|
|
|
2 |
þ |
|
|
|
|
||||||||
|
ì |
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
|
1 ö |
|
2 |
ü |
ì |
|
|
|
1 |
|
|
|
|
ü |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
8. |
íx |
x Î R, (x +1)ç x |
- |
|
|
÷ |
(x |
|
|
- 2) = 0ý |
= í-1, |
|
|
, - |
2, 2ý |
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
î |
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
2 ø |
|
|
|
þ |
î |
|
|
|
2 |
|
|
|
|
þ |
||||||||
Н айдем пере с е ч ение двухмнож ес т в: 9. {x x ÎQ, x < 0}I{x x ÎQ, x > 0}
И зобразим нач ис л овойпрямойзаданные множ ес т ва:
|
|
x>0 |
|
x<0 |
|
|
|
0 |
x |
|
|
|
|
|
|
|
|
О ч е видно, |
ч т о |
множ ес т ва |
не |
пе рес екаю т с я, |
т .е. |
{x x ÎQ, x < 0}I{x x ÎQ, x > 0} = Æ
Проводя анал огич ные рас с уж дения, ре ш аю т с я с л едую щ ие задания: 10.{x x Î Z, x < 5}I{x x Î Z, x ³ 0} = {x x Î Z, x Î[0,5)}
11.Q I Z = Z
12.{x x Î Z, x £ 5}I{x x Î Z, x > -3} = {x x Î Z, x Î(-3,5]}
6
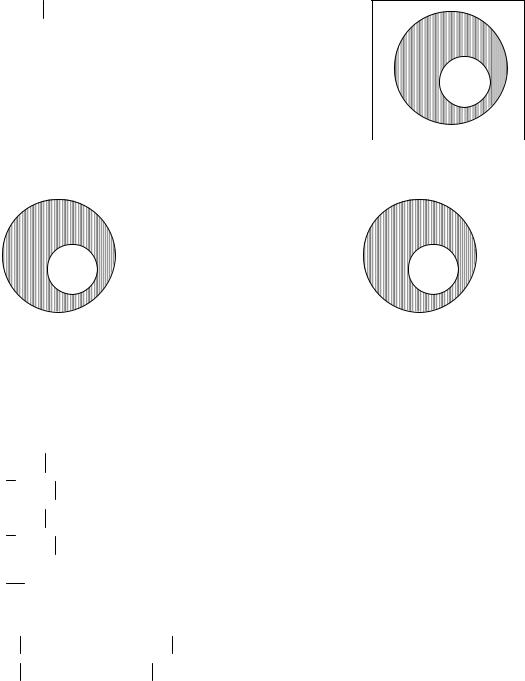
13. Н айдем и проил л ю с т рируем диаграммой разнос т ь с л е дую щ их мно-
же с т в:
a)N \{x x N, x = 2n}
М нож е с т во {x |
|
x N, x = 2n} |
- эт о множ ес т во нат у- |
N |
|||||||||||||
|
|||||||||||||||||
рал ь ныхч ет ныхч ис ел . Разнос т ь ю множ ес т вавс ех |
|
|
|
||||||||||||||
нат урал ь ныхи нат урал ь ныхч ет ныхч ис ел явл яет - |
x=2n |
||||||||||||||||
с я |
множ е с т во нат урал ь ны х неч е т ных ч ис е л , т .е. |
|
|
|
|||||||||||||
N \{x |
|
x N, x = 2n} = {x |
|
x N, x = 2n −1} . |
|
|
|
||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
b) |
|
|
= NZ \ UN{0} _ |
c) Z \ {x |
|
x Z, x ≤ 0} = N |
|
|
|
||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
N_ |
|
|
|
|
|
|
N |
|
||||||
|
|
|
|
|
|
||||||||||||
c) |
K \ P , где |
K – множ ес т во т оч екпл ос кос т и, рас с т ояние от кот орыхдо |
|||||||||||||||
|
т оч ки О |
не превыш ает |
2 с м, P – множ ес т во т оч ек пл ос кос т и, рас - |
||||||||||||||
с т ояние кот орыхот т оч ки О ме нь ш е 2 с м.
М нож ес т во K – эт о круг радиус а2 с м, P – множ е с т во т оч ек внут - реннос т и кругабез окруж нос т и. K \ P - окруж нос т ь .
14.Н айде м допол нения множ ес т в:
a.A = {x x N , x < 5} до множ е с т ваN AN = {x x N, x [5, +∞)}
b.A = {x x N,10 ≤ x < 20} до множ е с т ваN
AN = {x x N, x [1,10)U[20, +∞)}
c. М нож ес т во нат урал ь ныхч ис е л до множ ес т вацел ыхч ис е л
NZ = {0}U{N _}
d. М нож ес т во цел ыхч ис е л промеж ут ка[−3,10) до множ ес т ваZ
{x x Z, x [−3,10)}Z = {x x Z, x (−∞,−3)U[10,+∞)}
e.{x x Q, x < −20}Q = {x x Q, x [−20,+∞)}
§3. Числ ов ы е посл едов а тел ьности.
П римерами ч ис л овы х пос л едоват ел ь нос т е й могут с л уж ит ь пос л едоват ел ь нос т и вс ехч л енов арифмет ич ес койи ге омет рич е с койпрогре с с ий.

7
Опр едел ение 1. Е с л и каж дому ч ис л у n из нат урал ь ного рядач ис ел 1, 2, 3,… , n,… пос т авл ено в с оот вет с т вие вещ ес т венное ч ис л о xn , т о множ е с т во
ве щ ес т венны хч ис е л
|
|
|
|
|
|
31 2 xn ,... x x ,..., , , |
|
|
|
|
|
(1) |
||
называет с я чис ло во й по с л едо ва тел ьно с тью . |
|
|
|
|
|
|
|
|||||||
Ч ис л а |
31 |
2 xn ,... будеx x м,...называт, , , |
ь э лем ента ми ил и чл ена м и по с ле- |
|||||||||||
до ва тельно с ти (1), |
с имвол |
xn |
– общ им эл е мент ом пос л едоват ел ь нос т и, а |
|||||||||||
ч ис л о n – его номером. |
|
|
|
|
|
|
|
|
|
|
||||
Сокращ е нно пос л едоват ел ь нос т ь (1) буде м обознач ат ь с имвол ом {xn }. |
||||||||||||||
Н априме р, с имвол íì |
1 |
ýü обознач ае т пос л едоват е л ь нос т ь : 1, |
1 |
, |
1 |
, ..., |
1 |
, ... |
||||||
|
|
|
|
|||||||||||
|
|
înþ |
|
|
|
2 |
|
3 |
n |
|||||
П ос л е доват ел ь нос т ь с ч ит ает с я заданной, е с л и указан с пос об пол уч е - |
||||||||||||||
ния л ю бого ее эл е мент а. |
|
(=- 1+)n задает пос л едоват ел ь нос т ь 0, 2, 0, 2,… |
||||||||||||
Н априме р, формул а xn |
1 |
|||||||||||||
П о с амому определ е нию |
пос л едоват ел ь нос т ь с одерж ит бе с конеч ное |
|||||||||||||
ч ис л о эл е мент ов: |
л ю бы е два е е эл е мент а от л ич аю т с я, |
по крайне й мере, |
||||||||||||
номерами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Геомет рич ес ки |
пос л едоват ел ь нос т ь |
изображ аю т |
на координат ной |
|||||||||||
прямой в виде пос л едоват ел ь нос т и т оч ек, координат ы кот орых равны с о- от вет с т вую щ им эл емент ам пос л е доват ел ь нос т и.
|
А р ифм етическ ие дей ств ия на дчисл ов ы м и посл едов а тел ьностям и. |
|||
|
П ус т ь даны пос л едоват ел ь нос т и {xn } и {yn }. |
|
||
1. |
П роизве дением пос л едоват ел ь нос т и |
{xn } нач ис л о m назовем пос л едо- |
||
ват ел ь нос т ь : |
31 mx2 n ,... , т .еmx. |
,...{,n }mx, { ×,× xmxn }m.= m |
x |
|
2. |
Ал гебраич е с кой с уммой данны х пос л едоват е л ь нос т ей называет с я по- |
|||
с л едоват ел ь нос т ь : |
3 |
3 n ±2 yn ,1...2 x, т1.е±. y |
x,±...y, , x x y , |
|
{ } { } { ±± yn }=xn
3. П роизве дением:
4. Ч ас т ным: |
x1 |
|
x2 |
|
x3 |
y1 |
|
y2 |
|
y3 |
|
|
|
|
yn
xn
yn
|
3 |
3 |
n ×2 yn ,12...x, 1т .×еy. { x },×...y{, ,xx} {y ××,yn } x=xnn yn |
||||
... т,. е . |
{x } |
|
ì x |
|
ü |
|
|
...n, |
} |
=, |
í |
n, |
ý |
y,n ¹ . 0 |
|
|
{yn |
|
î yn þ |
|
|||
Опр едел ение 2. П ос л едоват е л ь нос т ь {xn } называет с я огранич е ннойс верху
(с низу), ес л и с ущ ес т вует ч ис л о М |
(m) т акое |
ч т о, л ю бой эл е ме нт |
эт ой по- |
|||
с л едоват ел ь нос т и удовл ет воряет неравенс т ву |
n £ |
( n ³ m). xx |
M |
|||
ил и |
( ): |
{ } |
( n ³Mm). x n n£ |
n Þx$ Îx "x M m |
||
Опр едел ение 3. П ос л едоват е л ь нос т ь {xn } называет с я огранич е нной, е с л и
онаогранич е нас верху и с низу, т .е. с ущ ес т вую т ч ис л а m и |
M т акие ч т о, |
л ю бой эл емент эт ой пос л едоват ел ь нос т и удовл ет воряет |
нераве нс т ву |
£ n £ Mm . x |
|
8
Опр едел ение 4. П ос л едоват е л ь нос т ь {xn } называет с я нео гра ниченно й, е с л и
дл я л ю бого пол ож ит ел ь ного ч ис л а А с ущ ес т вует эл е мент |
xn эт ойпос л едо- |
||||
ват ел ь нос т и, удовл ет воряю щ ий нераве нс т ву |
|
xn |
|
> A, т .е. |
л ибо xn > A , л ибо |
|
|
||||
xn < -A. |
|
||||
Пр им ер ы .
1. {n} = {1, 2, 3, ..., n,...} – огранич енас низу, но не огранич енас верху m = 1, т .е. xn ³ 1.
2. |
{-n} = {-1, - 2, - 3, ..., - n,...} - огранич ена с верху, но не огранич ена с низу |
||||||||||
M = −1, т .е. xn £ -1. |
|||||||||||
3. |
íì1, |
1 |
, |
1 |
, ..., |
|
1 |
, ...ýü - огранич е на, " xn Î{xn }: 0 £ xn £1. |
|||
2 |
|
|
|||||||||
|
î |
3 |
|
|
|
n |
|
þ |
|||
4. |
{-1, - 2, - 3, - 4, - 5,..., (-1)n ,...} – неогранич енная, т аккаккакого бы не был о |
||||||||||
ч ис л о |
|
A , с реди эл еме нт ов эт ой пос л е доват е л ь нос т и найдут с я т акие эл е - |
|||||||||
мент ы, ч т о: |
|
|
xn |
|
> A . |
||||||
|
|
||||||||||
Опр едел ение 5. П ос л едоват ел ь нос т ь {xn } называет с я б ес ко нечно б о льшо й,
ес л и дл я л ю бого пол ож ит ел ь ного ч ис л а А с ущ ес т вует номер N т акой, ч т о дл я вс ехэл еме нт ов пос л едоват ел ь нос т и с номерами n > N выпол няе т с я не -
равенс т во |
|
xn |
|
> A, например, {n} = {1, 2, 3, ..., n,...}, {n2} = {1, 4, 9, ..., n2 ,...}. |
||||||
|
|
|||||||||
Символ ич ес кая запис ь |
опреде л ения бес коне ч но бол ь ш ой пос л едова- |
|||||||||
т е л ь нос т и: ( |
0)( ): ( |
) |
|
n |
|
> A . Þx > N"A n $"N > |
||||
|
|
|||||||||
Опр едел ение 6. П ос л едоват е л ь нос т ь {αn } называе т с я |
б ес ко нечно м а ло й, |
|||||||||
ес л и дл я л ю бого пол ож ит ел ь ного ч ис л аε с ущ ес т вует |
номер N т акой, ч т о |
|||||||||
дл я вс ехэл еме нт ов пос л едоват ел ь нос т и с номерами n > N выпол няе т с я не -
равенс т во |
|
αn |
|
< ε , например, |
íì |
1 |
ýü , íì |
1 |
ýü . |
|
|
|
|||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
în |
þ în3 |
þ |
|
|
|
||||||
Символ ич ес кая запис ь опре дел ения бес конеч но мал ой пос л е доват е л ь - |
|||||||||||||||||||||
нос т и: ( |
0)( |
):ε( |
N N ) n |
|
|
n |
|
|
< ε . |
Þα > " |
|
$" > |
|||||||||
|
|
|
|
||||||||||||||||||
Т еор ем а . |
Е с л и |
{xn } |
– бес коне ч но бол ь ш ая пос л едоват ел ь нос т ь , и вс е ее |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì |
1 |
ü |
|
ч л е ны от л ич ны от нул я, т о пос л едоват ел ь нос т ь |
í |
ý - бес конеч но мал ая, и |
|||||||||||||||||||
|
|||||||||||||||||||||
обрат но, ес л и {αn } |
|
|
|
|
|
|
|
|
|
|
î |
хn þ |
|||||||||
- бес коне ч но мал ая пос л едоват ел ь нос т ь и αn ¹ 0 , т о по- |
|||||||||||||||||||||
|
|
|
|
|
|
ì |
|
1 |
ü |
|
|
|
|
|
|
|
|
|
|
|
|
с л едоват ел ь нос т ь í |
|
ý - бе с конеч но бол ь ш ая. |
|
|
|
||||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
îαn þ |
|
|
|
|
|
|
|
|
|
|
|
||||

9
§4. Пр едел посл едов а тел ьности.
Опр едел ение 1. П ус т ь a - некот орая т оч канаос и и δ - не кот орое пол ож и- т е л ь ное ч ис л о. Т огдал ю бой проме ж ут ок вида(a -δ ,a +δ ) , будем называт ь
о крес тно с тью |
ил и |
δ-окре с т нос т ь ю т оч ки a . |
|
|
||||||||||||||
|
|
|
|
|
|
|
0 |
а-d |
|
|
а |
а+d |
|
|
||||
|
Ут верж дение |
x δ -окрес т нос т и т оч ки a эквивал ент но выпол не нию |
||||||||||||||||
нераве нс т ва |
|
x - а |
|
£ δ . |
|
|
|
|
|
|
|
{xn } , |
||||||
|
|
|
|
|
|
|
|
|
||||||||||
Опр едел ение 2. Ч ис л о а называет с я пре дел ом пос л е доват е л ь нос т и |
||||||||||||||||||
ес л и дл я л ю бого пол ож ит ел ь ного ч ис л аε с ущ ес т вует |
номер N т акой, ч т о |
|||||||||||||||||
при n > N выпол няет с я неравенс т во |
|
xn - a |
|
< ε . |
|
|
||||||||||||
|
|
|
|
|||||||||||||||
|
С |
помощ ью |
|
с имвол ов |
эт о |
опреде л ение |
мож но запис ат ь : |
|||||||||||
( ε 0)( |
): ( |
|
) |
|
n a |
|
< xε -. N NÞn > " $" > |
|
|
|||||||||
|
|
|
|
|
||||||||||||||
|
П ос л е доват е л ь нос т ь, име ю щ ая преде л называет с я с хо дящейс я. |
|
||||||||||||||||
|
Е с л и пос л едоват ел ь нос т ь с ходит с я и име ет с воим предел ом ч ис л о a , |
|||||||||||||||||
т о с имвол ич е с ки эт о запис ывае т с я: xn ® a |
при n → ∞ ил и lim xn = a . |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
П ос л едоват ел ь нос т ь , |
не явл яю щ аяс я с ходящ е йс я, называе т с я ра с хо - |
||||||||||||||||
дящ ейс я. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Св ой ств а сходящ |
ихся посл едов а тел ьностей |
|
||||||||||||
1. |
Сходящ аяс я пос л е доват е л ь нос т ь име ет т ол ько один предел . |
|
||||||||||||||||
2. |
Сходящ аяс я пос л е доват е л ь нос т ь огранич е на. |
|
|
|||||||||||||||
3. |
Сумма (разнос т ь ) двух с ходящ ихс я |
пос л едоват ел ь нос т е й {xn } и |
{yn} |
|||||||||||||||
ес т ь с ходящ аяс я пос л едоват ел ь нос т ь , пре дел кот орой раве н с умме (разно- с т и) пре дел ов пос л е доват е л ь нос т ей {xn } и {yn } .
4. |
П роизве дение двух с ходящ ихс я пос л едоват ел ь нос т е й {xn } и {yn } |
ес т ь |
|
с ходящ аяс я пос л е доват ел ь нос т ь , преде л кот орой равен произведению |
пре - |
||
дел ов пос л едоват ел ь нос т е й{xn } и {yn } . |
|
|
|
5. |
Ч ас т ное двухс ходящ ихс я пос л е доват е л ь нос т ей {xn } |
и {yn } при ус л овии |
|
n→∞ yn ¹ 0 , е с т ь limс ходящ аяс я пос л едоват е л ь нос т ь , пре дел |
кот орой равен ч а- |
||
с т ному преде л ов пос л едоват ел ь нос т е й{xn } и {yn } . |
|
|
|
6. |
Е с л и эл емент ы с ходящ е йс я пос л едоват ел ь нос т и {xn } , нач иная с некот о- |
||
рого номера, удовл ет воряю т нераве нс т ву xn ³ b ( xn £ b ), т о и преде л а |
эт ой |
||
пос л едоват ел ь нос т и удовл ет воряет неравенс т ву a ³ b ( a £ b ). |
|
||

10
М онотонны е посл едов а тел ьности Опр едел ение 3. П ос л е доват е л ь нос т ь {xn } называе т с я:
возрас т аю щ ей, ес л и xn |
< xn+1 |
дл я вс ех n ; |
|
не убываю щ е й, ес л и xn |
£ xn+1 |
дл я вс ех n ; |
|
убываю щ ей, е с л и xn > xn+1 |
дл я вс ех n ; |
||
не возрас т аю щ е й, е с л и xn |
³ xn+1 дл я вс ех n . |
||
Вс е т акие пос л едоват ел ь нос т и объединяю т с я общ им название м м о но то н-
ны е по с ледо ва тел ьно с ти.
Пр им ер ы . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
1. |
1, 1 |
, 1 |
, ..., |
1 |
, ... - убываю щ ая и огранич е нная. |
|||||||||||
|
2 |
3 |
|
|
|
n |
|
|
|
|
|
|
|
|
||
2. |
|
1 |
1 |
, |
1 |
, |
1 |
, ..., |
1 |
, |
1 |
,... - невозрас т аю щ ая и огранич е нная. |
||||
, 1, , |
2 |
3 |
3 |
n |
n |
|||||||||||
|
|
2 |
|
|
|
|
|
|
|
|||||||
1. |
1, 2, 3,… |
… |
|
|
., n,… |
.. – возрас т аю щ ая и неогранич е нная. |
||||||||||
2. |
1 , |
2 , |
3 |
, ..., |
n |
|
, ... - возрас т аю щ ая и огранич енная. |
|||||||||
4 |
n +1 |
|||||||||||||||
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|||||
Т еор ем а . М онот онная огранич е нная пос л е доват е л ь нос т ь с ходит с я.
Рас с мот рим пос л едоват ел ь нос т ь {xn } с общ им эл емент ом |
æ |
|
1 |
ön |
||
xn = ç1 |
+ |
|
÷ |
. Э т а |
||
n |
||||||
|
è |
|
ø |
|
||
пос л едоват ел ь нос т ь |
|
с ходит с я |
и |
ее |
преде л |
равен |
|||||
|
|
|
æ |
|
1 ön |
|
|
|
|
|
|
x |
n |
= |
ç1 |
+ |
lim÷ = e |
elim» |
... |
7182, |
, 2 |
|
|
n |
n |
∞ → |
|
→∞ |
|
|
|
|
|
|
|
|
|
|
è |
|
n ø |
|
|
|
|
|
|
§5. Пр им ер ы р еш ения за да чна тем у«Числ ов ы е посл едов а тел ьности»
1. Н апис ат ь первые пят ь эл еме нт ов пос л е доват е л ь нос т и:
a) |
xn = |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
И с пол ь зуе м |
опреде л ение |
ч ис л овой |
пос л е доват ел ь нос т и |
n = |
5,.4, 3, 2,1 |
|||||||||||||
П одс т авл яем |
знач е ния в |
формул у |
общ его |
|
ч л е на xn , |
пол уч ае м: |
||||||||||||
1 ; |
2 ; |
3 ; |
4 ; |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b) |
xn = |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2n + 1 |
|
5,,4,имее3, 2,1 м: 1 ; |
1 ; |
1 |
|
1 ; |
|
1 |
|
|
|
|||||||
Анал огич но, пол агая n = |
; |
|
|
|
||||||||||||||
7 |
11 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
5 |
|
9 |
|
|
||||
2. Н айт и формул у общ его эл еме нт апос л едоват ел ь нос т и:
a) |
1; |
1 |
; |
1 |
; |
1 |
; |
1 |
;... |
|
|
|
3 |
5 |
7 |
92 |
2 |
2 |
|||||||
|
|
|
|
|
|
