Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

may05119

.pdf

Скачиваний:

Добавлен:

21.05.2015

Размер:

670.28 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Разрывы функцийкл ас с ифицирую т с я с л е дую щ им образом:

1. У стр а ним ы й

р а зр ы в .

Т оч ка x0 называе т с я то чко й ус тра ним о го

ра зры ва функции f (x) , е с л и

пре дел в эт ой т оч ке с ущ ес т вует , но в т оч ке

функция л ибо не опреде л е -

на, л ибо ее знач ение не равно предел у в эт ойт оч ке.

Н апример, функция y =

x2 - x

. Рас с мот рим т оч ку x0 = 1. Н айде м пре дел в

x -1

- x

x(x -1)

- x

, x ¹ 1

эт ойт оч ке

lim

= lim

=1. Ф ункция

- ус т раняе т раз-

y = í x -1

-1

x -1

x→1

рыв.

îx, x = 1

2. Ра зр ы в

1 р ода .

f (x), е с л и в эт ой

Т оч ка x0 называе т с я т оч кой разрыва1 родафункции

т оч ке функция

f (x)

имее т конеч ные, но не равные друг другу правыйи л е -

выйпреде л ы:

lim f (x) ¹ lim f (x) .

x→x0+

x→x0−

3. Ра зр ы в

2 р ода .

f (x), е с л и в эт ой

Т оч ка x0 называе т с я т оч кой разрыва2 родафункции

т оч ке функция

f (x)

не имеет , по крайне й ме ре,

одного из однос т оронних

пре дел ов ил и хот я бы один из однос т оронних преде л ов бе с конеч е н. Н а-

приме р, дл я функции f (x) = 1					т оч ка x = 0	явл яет с я т оч кой разрыва2 рода,
				x
т аккак lim		1 = +¥ , аlim f (x) = -¥ .
	x→0+ х			x→0−
			Н епр ер ы в ностьфунк ции на отр езк е
	Ф ункция		f (x)	непрерывнанаинт ервал е (a,b), е с л и онане прерывнав
каж дойт оч ке эт ого инт ервал а.
	Ф ункция		f (x)	непре рывнанас е гмент е [a,b] , е с л и онанепрерывнана
инт ервал е		(a,b) и		непрерывна в т оч ке а		с права и в т оч ке b с л ева, т .е.
→ +	( ) =	( )	lim	(, )= (b)f.	x limf	a f f x
			→b− x		x a

Св ой ств а непр ер ы в ны хфунк ций

1. Пер в а я теор ем а Бол ьца но-К ош и (т еоремао прохож дении функции ч ерез нул евое знач ение при с мене знаков).


П ус т ь функция	= y(x)f не прерывнанаот ре зке [a,b] и наконцах от резка
имее т знач ения разных знаков, т .е.		( )× (b)f<f0a.	Т огдас ущ е с т вует	т оч ка
c Î[a,b] , в кот орой f (с ) = 0 .
2. Пер в а я теор ем а В ей ер ш тр а сса		(т еорема об	огранич е ннос т и	не пре -
рывнойфункции наот ре зке)
Е с л и функция	f (x) опре дел енаи непрерывнанаот резке [a,b] , т о онаогра-

нич е нанаэт ом от ре зке.

Г л а в а 3. Пр оизв одна я. Д иффер енциа л .

§1. Понятие пр оизв одной .

П ус т ь нанекот ором промеж ут ке Х заданафункция

= y(x)f. Возь ме м

произвол ь ную

т оч ку x0 X

и придадим аргумент у х в т оч ке x0

произвол ь -

ное приращ е ние x , т акч т обы x0 +

x X .

Опр едел ение 1. П рира щением функции

= y(x)f в т оч ке

x0 , от веч аю щ ему

приращ е нию

x , будем называт ь ч ис л о

y x0 f

х − f

x0+() . (

Опр едел ение 2. П ро изво дно й функции

= y(x) f в т оч ке

называе т с я пре -

дел от нош е ния приращ ения функции кприращ ению

аргумент апри x → 0 ,

и онаобознач ает с я

′

0 +

− x0()f

( x )f x

lim

f (x) =

lim

x → 0

П роцес с нахож де ния производнойназывает с я диффере нцированием.

Возь ме м

на ис с л е дуе мой кривой

(с м.

рис унок)

(

две

т оч ки

М 0:

f (x0+ x)

x fM x

M 0

(

( ))

( 0 ,

x+)). , 0xП+f0ро0x- 0 x M

ве дем

ч ерез М

М 0

с екущ ую ,

обра-

зую щ ую

с ос ь ю 0хугол

ϕ .

f (x0)

f .

И з

MM0N

tgϕ =

Ус т ре мим

x → 0 .

П ри эт ом т оч ка

x0+

М 0 будет

с кол ь зит ь по кривой, прибл и-

ж аяс ь

к т оч ке

М ,

ас екущ ая М М 0, пос т е пенно меняя с вой угол

накл она,

буде т с т ре мит ь с я

к некот орому «пре дел ь ному» пол ож е нию , называемому

ка с а тельно й к криво й в т оч ке М . А знач ит угол ϕ → α .

Гео м етричес кий

с м ы с л

про изво дно й:

f '(x)

в каж дой т оч ке

х равна

т анге нс у угл анакл онакас ат ел ь нойкграфику

f ( x ) :

tgα = lim tgϕ = lim

′

= f (x) = k ,

x→0

где k

– угл овой коэффициент

кас ат ел ь ной к графику функции y = f (x) , в

т оч ке с координат ой x0 .

Уравне ние кас ат ел ь нойкграфику функции y = f (x) имее т вид: y (x) = y (x0 ) + y '(x)(x − x0 ).

Опр едел ение 3. Ф ункция y = f (x) называет с я дифференцируемо й в т оч ке x0 , ес л и е е приращ ение в эт ойт оч ке мож но пре дс т авит ь в виде:

y = A x +α ( x) x ,

где А- некот орое ч ис л о, не завис ящ е е от x ;

α ( x) – бес конеч но мал ая функция, при x → 0 .

Т еор ем а 1. Д л я т ого, ч т обы функция y = f (x) был адифференцируемав т оч ке x0 , необходимо и дос т ат оч но, ч т обы онаимел ав эт ой т оч ке конеч -

ную производную .

Т еор ем а 2. Е с л и функция дифференцируе мав даннойт оч ке x0 , т о онане - прерывнав эт ойт оч ке.

Е с л и

x = a

Пр а в ил а диффер енцир ов а ния

a = const , т о f

(x) º 0 ,

т(.е.) производна, я пос т оянной равна

′

нул ю .

f ( x ) = u( x ) ± v( x ) ,

т о

f (x) = u (x) ± v (x) ,

т .е.

производная

ал геб-

Е с л и

′

раич ес кой

с уммы

дифференцируемых функций

равна ал ге браич ес кой

с умме производны хэт ихфункций.

3. Е с л и f (x) = u(x)×v(x) , т о ( )

( )

( )× ' (x)=.v+ x u× '

x v ' x uf x

П роизводная

с л ож ной

функции:

ес л и

(

) =

( (x))f,

FG тxо

′

G (x) = F ( f (x))× f (x) .

Т а бл ица пр оизв одны х

1. (x ) = n × x

−1

)

' = e

(cos x)

= -sin x

′

(arcsin x)¢ =

1- x2

(sin x)¢ = cos x

(arccos x)¢ = -

- x2

10.

(tgx)¢ =

(arctgx)¢ =

cos2 x

1+ x2

11.

(arcctgx)' = - 1 + x2

(ctgx) = - sin2 x

6. (ax )¢ = ax ln a

§2. Пр им ер ы р еш ения за да чпо тем е «Пр оизв одна я функ ции».

Пр остей ш ие сл уча и на хождения пр оизв одной .

x +31 x-=y2 x+

xy=- 2 x+ 6

+ 4=. -Д л я+ удобс т ванахож дения производной пе репи-

ш е м функцию в с л едую щ ем виде :

−1

3x−2 + 4x.y

−=x

−1

−

−1 −2

−1

−31

−2

6x−3

xy=

x+ -

x 3

33 x2

- 5=ctgx -cos4

sin x3+y=

20x+

sin 2

tgx

	1			24
y ex			x3	+ x + 2 ln= -
	2cos2	x

II.Н а хождение пр оизв одной пр оизв едения, ча стного дв ухфунк ций .

x sin x y

(

)

(

)

(

e+ x

cos=e x

e +sinx

+ cos x)

xsin

y =

arcsin x

(

)

x - arcsin x

× x' x

1- x2arcsinx

y'=

- 1arcsin- arcsin xx

1- x2

3arctgx

'= 3

+ x3

arctgx y

1+ x2

III.

Н а хождение пр оизв одной

сл ожной

функ ции.

П ус т ь

G - с л ож ная функция, т .е. G = G (x) , где

x = ϕ(t). Т огда

(Gn (x))' = n ×Gn−1 (x)×G '(x)

(arcsin G (x))' =

×G '(x)

1- G2 (x)

(cos G (x))' = -sin G (x)×G '(x)

(arccosG (x))' = -

×G '(x)

- G2 (x)

(

)) =

(

)×

'(x)

G x

Gcos

(arctgG (x))' =

×G '(x)

1+ G2 (x)

G' x

sin


4.	(tgG (x))' =	1			×G '(x)
			cos2 G (x)
		1
5.	(ctgG (x))' = -					×G '(x)
				sin2 G (x)
6.	( ( ) ) =	(x) G ×G 'x' (x) Galna					a

				1
10.			(x) ' = -	arcctgG(	× G' (x) )
				1 + G 2 (x)
11. (	( )	)' =	(x) G	G x	e
11. (		)' =	×	' (xe) G	e

т .е . каж дыйраз производная функции умнож ае т с я напроизводную аргуме нт а.

y =

6x sin

= (

) (

) =

6x cos' y 6

x 6'x

sin

(

=yx +1)x-

( 2

)2 ( 2

)

( 2

)2 ( x -1)

2x +1x-

=3x'+1x- × y=x +1x-

' 3

10.

y =

cos x

y '

(

x)'

1cos(

sin x)

-tgx=

cos x

11.

cos x

= 5

×sin xy

−

cosinx(

xsin

cos x

xsiny x + cosx

sin=

(sin

)'x

xç

x÷

è 5x

12.

y = tg (x2 +1)

y =

2 ( )'×=1 +

x2 + )1

(

cos

(

cos

§3. Пр оизв одны е в ы сш ихпор ядк ов . Диффер енциа л

П роизводная функции = y(x)f т акж е явл яет с я новой функцие й т ого ж е аргуме нт а. П роизводная е е называет с я производнойвт орого порядкапо от нош е нию кис ходнойфункции, т .е.

y '' = (y '(x))' , y ''' = ( y ''(x))'

Пр им ер .

Д анафункция y = x5 . Н айт и производную т рет ь его порядкаy '.'

y ' = 5x4 ; y '' = 20x3 ; y ''' = 60x2 .
Д л я диффере нцируемой функции			y = f (x) ее		приращ е ние мож но
пре дс т авит ь в виде : Dy = A×Dx +α (Dx) Dx ,			где	α (Dx)	–	бе с конеч но мал ая
функция, при	x → 0 .
Опр едел ение.	Дифференциа ло м dy ил и df (x)			функции		y = f (x) в т оч ке	x
называе т с я гл авная л ине йная от нос ит ел ь но x				ч ас т ь приращ ения функции
в эт ойт оч ке, т .е .			x .y x	f
	=	′
		( )				= ( )dx y-xформулf	а
П риращ ение аргуме нт а x обознач им как dx и т огда

′

диффере нцирования.

Пр им ер .

y = x3 + 4x2 . Н айт и dy . y ' = 3x2 + 8x

dy = (3x2 + 8x)dx

Д ифференциал функции dy явл яе т с я функцие й т ого ж е аргуме нт а. Д иффе - ренциал от эт ой функции называе т с я диффе ренциал ом вт орого порядка ис ходнойфункции, т .е. d (dy) = d 2 y .

Г л а в а 4. Пр им енение диффер енциа л ьног о исчисл ения к иссл едов а - нию функ ций

§1. Основ ны е теор ем ы диффер енциа л ьного исчисл ения

Т еор ем а Ф ер м а .
П ус т ь функция		= y(x)fопреде л е нанаинт ервал е a b() и, в не кот оройт оч ке
x0 эт ого	инт ервал а имеет		наибол ь ш е е ил и		наимень ш е е	знач е ние, т .е.
x b()a,,	£	x0 )f ил(f иx(	)	³ x0 )f . Т(f огдаx( ) ,	е с л и в т оч ке	x0 с ущ ес т вует
производная, т о онаравнанул ю , т .е. f x0 = 0 .					) '(
Т еор ем а Рол л я.
П ус т ь наот резке		a b[] опреде,		л енафункция = y(x)f, прич е м:

1.f (x) не прерывнана a b[] .,

2.f (x) дифференцируемана a b() .,

3.= b)f.( f (a)

Т огдас ущ е с т вует т оч кас a b() ,,в кот орой f		c = 0 . ) '(
Т еор ем а Л а гр а нж а .
П ус т ь наот резке a b[] опреде,	л енафункция	= y(x)f, прич е м:

1.f (x) не прерывнана a b[] .,

2.f (x) дифференцируемана a b() .,

Т огда с ущ ес т вует т оч ка c b()a, т акая, ч т о с праведл ива формул а

−a)f ( f (b) .

=f c) '(

b - a

§2. М	онотонностьфунк ции. Э к стр ем ум функ ции и его на хожде-
ние
Т еор ем а .	Ес л и функция	f (x) диффере нцируема на инт е рвал е			a b() , и
f x > 0 ()f'( x < 0 ),)т'о( функция возрас т ает (убывает ) наинт ервал е					a b() .,
Т еор ем а .	Ес л и функция	f (x) диффере нцируема на инт е рвал е			a b() , и
f x ³ 0 ()f'( x £ 0 ),)т'о( функция не убывает (не возрас т ает ) на a b() .,
Опр едел ение. Т оч ка x0 называе т с я т оч кой с тро го го				ло ка льно го м а кс им у-
м а (м иним ум а ) функции		f (x) , ес л и дл я вс ехх из некот орой δ-окрес т нос т и
т оч ки x0 выпол няет с я неравенс т во			< x0 )f (f x( )>	x0 )f) при(f x( х)¹х0 .
	y		y
			max
	min

0 x0 -δ	x0 x0 +δ	x	0	x0 -δ	x0 x0 +δ	x

Л окал ь ны ймакс имум (max) и л окал ь ны йминимум (min) объе диня- ю т с я общ им названием ло ка льны й э кс трем ум .

Т еор ем а (необходимое ус л овие л окал ь ного экс т ре мума).

Е с л и функция

f (x) имее т

в т оч ке

л окал ь ны й экс т ремум и диффе -

ренцируе мав эт ойт оч ке , т о f

x0 = 0 .

)

Э т и

т оч ки

называю т

с та цио на рны м и,

ил и

то чка м и

во зм о ж

но го

э кс трем ум а .

Е с л и т оч ка x0

- т оч кавозмож ного экс т ремума, т .е .

= 0 , т) о'(она

мож е т и не быт ь т оч кой л окал ь ного макс имумаил и минимума. Н апример,

y = x3 , y =

x2 = 0

при' 3 x = 0 , но, т е м не ме нее,

в т оч ке x = 0

нет л окал ь ного

экс т ремума.

Т еор ем а ( дос т ат оч ное ус л овие л окал ь ного экс т ремума).

Е с л и функция

диффере нцируемав некот орой δ-окрес т нос т и т оч ки

x0 . Т огда,

е с л и

> 0

)('(f x

< 0 ) )дл'(я вс ех из x0 − δ(

x0 )

(,с л еваот т оч ки

x0 ), а f

< 0

() f'(

> 0 ) )дл'(я вс ех из

x0 + δ ) (с(права,

от

т оч ки x0 ),

т о в

т оч ке x0

функция

f (x) име ет

л окал ь ны й макс имум (минимум). Е с л и ж е

x) '(во вс е й δ-окрес т нос т и т оч ки x0

име ет один и т от

ж е знак, т о в т оч ке

л окал ь ного экс т ремуманет .

Д ругими

с л овами,

е с л и

f x) '(при

переходе ч ере з т оч ку

x0 меняет

знак с «+» на«-», т о x0 - т оч кал окал ь ного макс имума;

ес л и

x) '(при пе -

реходе ч ере з т оч ку x0 меняет

знак с

«-» на«+», т о x0

- т оч кал окал ь ного

минимума; ес л и

x) '(при переходе ч ере з т оч ку x0

знакане меняет ,

т о в

т оч ке x0

экс т ре мумане с ущ ес т вует .

Пр им ер .

x + =)1.x −(f)1x

( ( )

Н айт и т оч ки л окал ь ного экс т ре мумафункции

Реш ение .

Н айдем производную :

x − )1.

Н айдем

x 5(+

)1x −( )( =1 x − )1x + ( )1+ x(+3= )1x − f )

x = 0

) '(

Реш ая уравнение

x x = 0x,−находим)1− 5(+)1 т ри( )(т 1оч ки возмож ного экс -

т ремумаx1 = −1,

= 1, x3

max

min

Знакf’(x)

-1

1/5

Знакf(x)

x =

- т оч каmax, x = 1 - т оч каmin, x = -1 - не явл яет с я т оч койэкс т ре мума.

§3. Н а пр а в л ение в ы пук л ости и точк и пер егиба

П ус т ь функция

= y(x)f диффере нцируеманаинт е рвал е

a b() .,Т огда

с ущ ес т вует

кас ат е л ь ная

графику

функции

= y(x)f

л ю бой т оч ке

xx))f эт((ого,

графика(

< ab ), xприч ем кас ат е л ь ная не парал л ел ь наос и

Oy , т аккаке е угл овойкоэффицие нт равны й f

x) ,'(конеч е н.

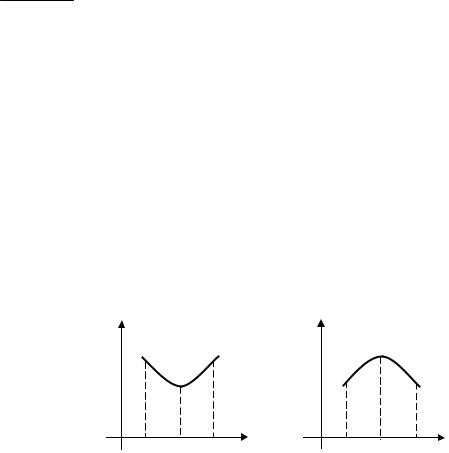
Опр едел ение 1.

Б удем

говорит ь ,

ч т о график функции

= y(x) f имее т на

a b()

,вы пукло с ть, на пра вленную вниз (вверх),

е с л и он рас пол ож е н не ниж е

(не выш е) л ю бойкас ат ел ь нойкграфику функции на a b() .,

вниз

вверх

Т еор ем а .

Е с л и функция

= y(x) f име ет на инт ервал е

a b() ,вт орую

производную и

³ 0

()

f'('

£ 0 ) во) '(' вс ех т оч ках a b() ,,т о графикфункции

= y(x)fиме -

ет на a b()

выпукл,

ос т ь, направл е нную вниз (вверх).

Опр едел ение 2.

Т оч ка М 0

x x0 ))f называет( ,

с я то чко й перегиб а

графика

функции

= y(x) f,

ес л и в т оч ке М

график име ет

кас ат ел ь ную

и с ущ ес т вуе т

т акая окре с т нос т ь т оч ки

x0 ,

в пре дел ах кот орой график функции

= y(x)f

с л еваи с праваот т оч ки x0

име ет разны е направл ения выпукл ос т и.

Т еор ем а (необходимое ус л овие т оч ки перегиба)

П ус т ь график функции

= y(x)f имее т

перегиб в т оч ке

x x0 ))f

и(пус, т ь

функция

= y(x)f имее т в т оч ке x0

не прерывную

вт орую производную . Т о-

гда f

x) в'('

т оч ке

x0 обращ ает с я в нул ь , т .е.

= 0 .

)

'('

Т оч ки М

x x0 ))f графика( , , дл я кот оры х f

= 0 ,

называю) '('

т с я крити-

чес кими.

Т еор ем а (дос т ат оч ное ус л овие т оч ки перегиба)

П ус т ь функция

= y(x)f имее т вт орую

производную

в некот оройокрес т но-

с т и т оч ки

x0 .

Т огда, е с л и в преде л ах указанной окре с т нос т и f

x) '('име ет

разны е знаки с л еваи с праваот т оч ки x0 , т о график

= y(x)f имее т пе ре гиб

в т оч ке М

x x0 ))f . ( ,

Пр им ер .

Н айт и т оч ки перегибафункции

( ) = 3

Н айдем производную : f

x) '(=

Н айдем вт орую производную :

='('-

. Вт орая производная в т оч ке

9x 3

x = 0 не с ущ ес т вуе т , но график функции

(

) = 3

имееf x т перегиб в т оч ке

) 0,, т(0аккаквт орая производная имеет с л еваи с праваразны е знаки.

перегиб

Знакf’’(x)

Знакf(x)

§4. А сим птоты г р а фик а функ ции

П ри ис с л е довании

пове дения

функции на бе с конеч нос т и, т .е. при

x → +∞ и при x → −∞ ил и вбл изи т оч ек разрыва2 рода, ч ас т о оказывает с я, ч т о график функции с кол ь угодно бл изко прибл иж ае т с я к т ой ил и иной

прямой. Т акие прямые называю т с я а с им пто та м и.

Сущ е с т вую т т ри

вида ас импт от :

вертика льны е,

го ризо нта льны е и

на кло нны е.

Опр едел ение 1. П рямая

x = x0

называе т с я вертика л ьно й а с им пто то й гра-

фикафункции

= y(x),f

ес л и хот я бы одно из предел ь ных знач ений

lim

ил и lim равно + ∞ ил и − ∞ .

x→ x0+

x→ x0−

Опр едел ение 2.

П рямая

y = A называет с я го ризо нта льно й а с им пто то й

графикафункции

= y(x)fпри x → +∞ ( x → −∞ ), ес л и

lim

( )= A .f

x→+∞

(x→−∞)

Опр едел ение 3.

П рямая

+ by, (kkx¹ 0) называет с я

на кло нно й

а с им пто -

то й графикафункции

= y(x)f при

x → +∞ ( x → −∞ ),

ес л и функцию

f (x)

мож но предс т авит ь

виде

( )

=+α+(x),

гдеb

kxα(xf)®x 0 при x → +∞

( x → −∞ ).

Т еор ем а .

Д л я т ого, ч т обы график функции

= y(x)f

имел

при

x → +∞ ( x → −∞ ) на-

кл онную ас импт от у

+ by,

необходимоkx

и дос т ат оч но, ч т обы с ущ ес т во-

вал и двапреде л а: lim

f (x)

= k

и lim [ (

) -

]= b .

x→+∞

(x→−∞)

Пр им ер .

x2 - 6x + 3

Н айт и ас импт от ы графикафункции y =

x - 3

Т оч ка

x = 3

т оч ка

разрыва 2

рода данной

функции, прич е м

lim

- 6x + 3

= -¥ , поэт ому прямая x = 3 - верт икал ь ная ас импт от а.

x - 3

x→3−

(x→3+ )

Н айдем накл онную ас импт от у, дл я эт ого,

ис пол ь зуя формул ы , определ им

знач е ния k и b :

f (x)

x2 - 6x + 3

k =

lim

lim= lim

= 1

x→+∞

1- x

(x→−∞)

- 3x

(x→−∞ )

- 3 +

6x + 3

- 3x + 3 =

[

(=) bkx]=

limx f-

- xlim= lim

lim

= -3

x→+∞

- 3

x→+∞

x - 3

x→+∞

(x→−∞ )

(x→−∞ )ë

(x→−∞ )

1 -

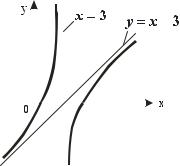
Т аким образом, пол уч аем,

ч т о график функции име ет

накл онную ас им-

пт от у:

y = x − 3.

§5. Общ а я схем а иссл едов а ния функ ций и постр оения гр а фик ов

О бщ ее ис с л едование функцийи пос т роение ихграфиков выпол няет - с я по с л едую щ ейс хеме :

1.Н айт и обл ас т ь опре дел ения.

2.О пре дел ит ь , явл яет с я л и функция ч ет ной, неч ет нойил и общ е го вида.

3.О пре дел ит ь явл яет с я л и функция периодич е с кой.

4. О пре дел ит ь явл яет с я л и функция непрерывнойил и найт и т оч ки разрыва и опреде л ит ь иххаракт ер.

5.Н айт и т оч ки пере с еч ения графикафункции с ос ями координат.

6.Н айт и ас импт от ы

7.Н айт и т оч ки возмож ного экс т ремума, инт е рвал ы возрас т ания и убывания функции.

8.Н айт и т оч ки пере гибаграфикафункции и инт е рвал ы его выпукл ос т и вверхи вниз.

9.П ос т роит ь графикфункции, ис пол ь зуя пол уч е нны е ре зул ьт ат ы ис с л е- дования.

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.05.2015694.81 Кб9malware_report_vimal_kumar.pdf
#
19.03.2016315.17 Кб5mar06012.pdf
#
20.05.2015401.41 Кб6MARINA_P_O.doc
#
20.05.201567.03 Кб61matan.docx
#
21.05.2015898.18 Кб11matmod.pdf
#
21.05.2015670.28 Кб6may05119.pdf
#
20.05.201583.51 Кб98MChP.docx
#
20.05.2015244.74 Кб47MChP_EKZ_Ch1_Ch2.doc
#
21.05.2015441.1 Кб8method_dynamics.pdf
#
21.05.2015975.4 Кб5method_statics.pdf
#
21.05.2015404.83 Кб15Metodicheskie_ukazania_po_Istorii_dlya_Matfaka.pdf