Задачи 31-40

Вычислить приближенное значение , заменяя приращение функциидифференциалом, если n = 6,

а =60.

Решение: Нужно вычислить приближенно .

Приращение функции в точке :.

Дифференциал функции в точке :.

При малых :или

Отсюда получаем общую формулу для приближенных вычисле­ний: , где .

В нашей задаче , где.

Найдем производную функции

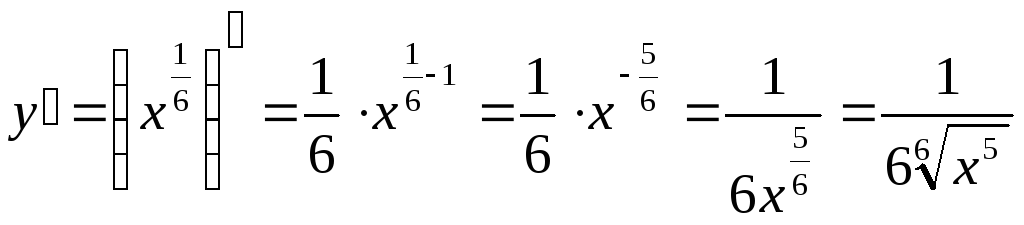
Приближенное равенство для функции будет иметь вид:

Здесь , в качестве выберем число 64, оно ближайшее , из которого точно извлекается корень шестой степени:

Следовательно,. Подстав­ляя в последнюю приближенную формулу , ,най­дем нужный результат:

Ответ:

Задачи 61-70 относятся к теме "Функции нескольких переменных". Для решения этих задач необходимо познакомиться со следующими вопросами названной темы:

1. Определение функции двух переменных, область определения функции, геометрическое изображение функции двух переменных.

2. Определение частных производных первого порядка для функции двух переменных, их вычисление.

3. Полный дифференциал функции двух переменных.

4. Производные высших порядков для функции двух переменных.

5. Определение локальных экстремумов для функции двух переменных.

6. Необходимое и достаточное условия экстремума для функции двух переменных.

7. Правило исследования на экстремум для функции двух переменных.

Задачи 41-50

Найти полный дифференциал функции двух переменных

Решение. Полный дифференциал функции двух переменных на­ходим по формуле:

где ;--частные производные данной функцииz.

Частные производные находим по обычным формулам дифферен­цирования для функции одной переменной, причем находим, счи­тая «у» постоянной величиной; аналогично при отысканиисчита­ем «х» постоянным:

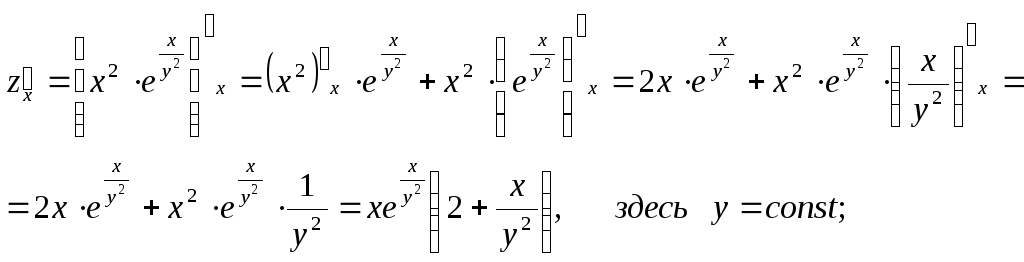
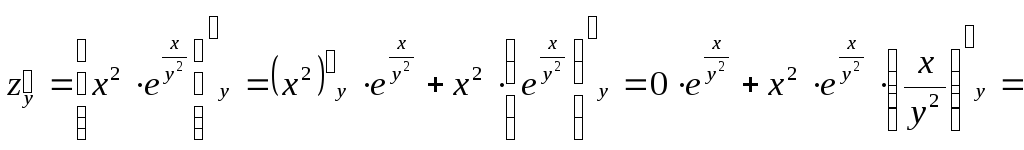
Отсюда полный дифференциал функции:

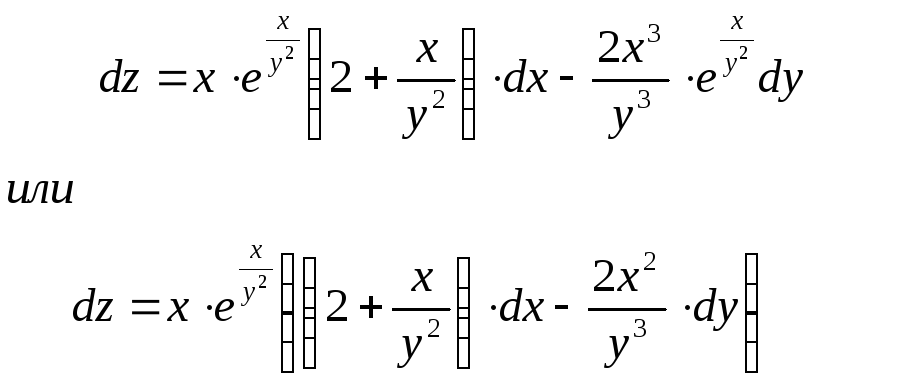
Задачи 51-60 и 61-70 относятся к теме «Интегральное исчисле­ние». Ознакомьтесь с основными вопросами этой темы:

1. Понятие первообразной и неопределенного интеграла.

2. Основные свойства неопределенного интеграла.

3. Таблица интегралов.

4. Основные методы интегрирования: непосредственное интегри­рование, интегрирование подстановкой, интегрирование по частям.

5. Интегрирование некоторых рациональных дробей.

6. Понятие определенного интеграла и его основные свойства.

7. Формула Ньютона-Лейбница для вычисления определенного интеграла.

8. Замена переменной и интегрирование по частям в определен­ном интеграле.

9. Применение определенного интеграла к вычислению площадей плоских фигур.

Интегрирование есть операция, обратная дифференцированию. ∫f(x)dx = F(x)+C, где F(х)-первообразная для подынтегральной функции f(x), то есть , аС - произвольная постоянная. При интегрировании часто используют свойства неопределенного инте­грала:

Идея интегрирования заключается в том, чтобы свести данный интеграл к одному из табличных интегралов. Поэтому, приступая к решению задач, ознакомьтесь с таблицей интегралов.

1.	1.
2.	2.
3.	3.
4.	4.
5.	5.
6.	6.
7.	7.
8.	8.
9.	9.
10.	10.
11.	11.
12.	12.
13.	13.
14.	14.
15.	15.
16.	16.

Примечание: Формулы интегрирования сохраняют свой вид при подстановке вместо независимой переменной любой дифференцируемой функции от нее, т.е. если

Tаким образом, применение основной таблицы сразу расширяется.

Например