2.3. Действующее значение синусоидального тока

Действующее значение синусоидального тока определяется по формуле:

.

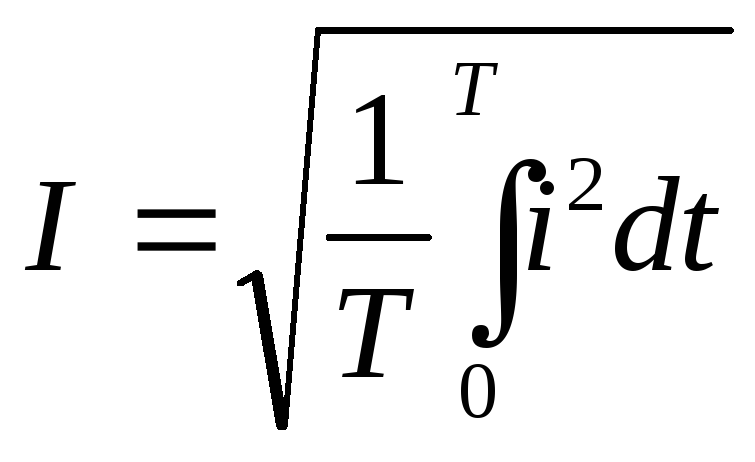При i = I_m sin ωt получаем

,

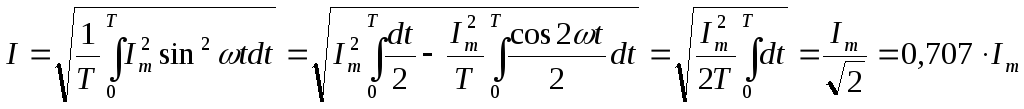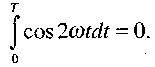
так как

Аналогично действующие значения э.д.с. и напряжений равны с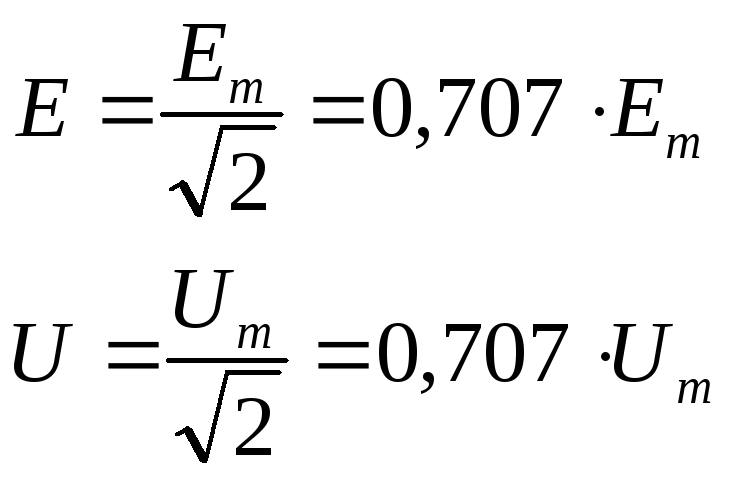оответственно

2.4. Среднее значение синусоидального тока

Под средним значением синусоидально изменяющейся величины понимают среднее значение ее за полпериода:

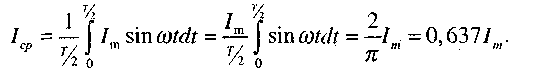
Аналогично средние значения э.д.с. и напряжений равны соответственно

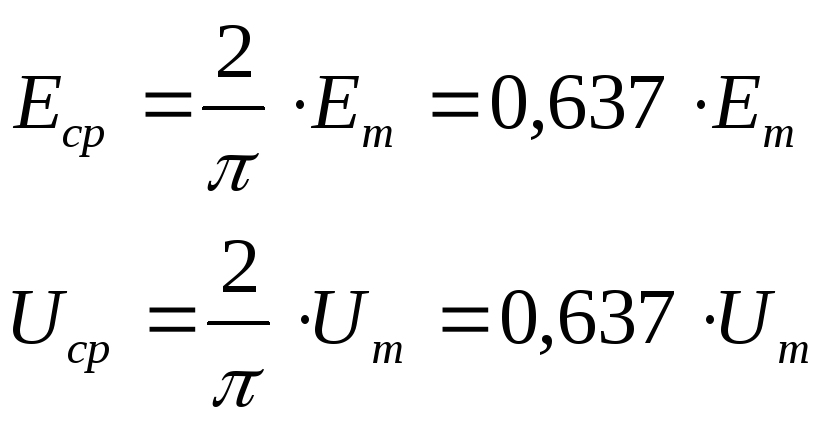
2.5. Цепь переменного тока с активным сопротивлением

Резистор R включен на синусоидальное напряжение U=U_msinωt (рис. 2.6), под действием напряжения по цепи протекает ток i. Величина сопротивления R переменному току больше, чем постоянному. При f = 50 Гц, = 1,01-1,05.

Рис. 2.6. Цепь переменного тока с активной нагрузкой

С увеличением частоты это отношение также увеличивается за счет поверхностного эффекта (скин-эффекта), эффекта вытеснения тока на поверхность проводника. Э.д.с. самоиндукции в проводниках переменного тока направлена навстречу току ,

где: L – индуктивность проводника;

–изменение тока во времени, поэтому плотность тока по сечению проводника неодинакова.

На переменном токе сопротивление резистора R называют активным, а на постоянном – омическим.

По закону Ома мгновенное значение тока в цепи (см. рис. 2.6):

,

т.е. напряжение и ток совпадают по фазе, а угол сдвига фаз равен нулю: φ=0.

На рис. 2.7 представлены графики изменения напряжения и тока в данной цепи и ее векторная диаграмма.

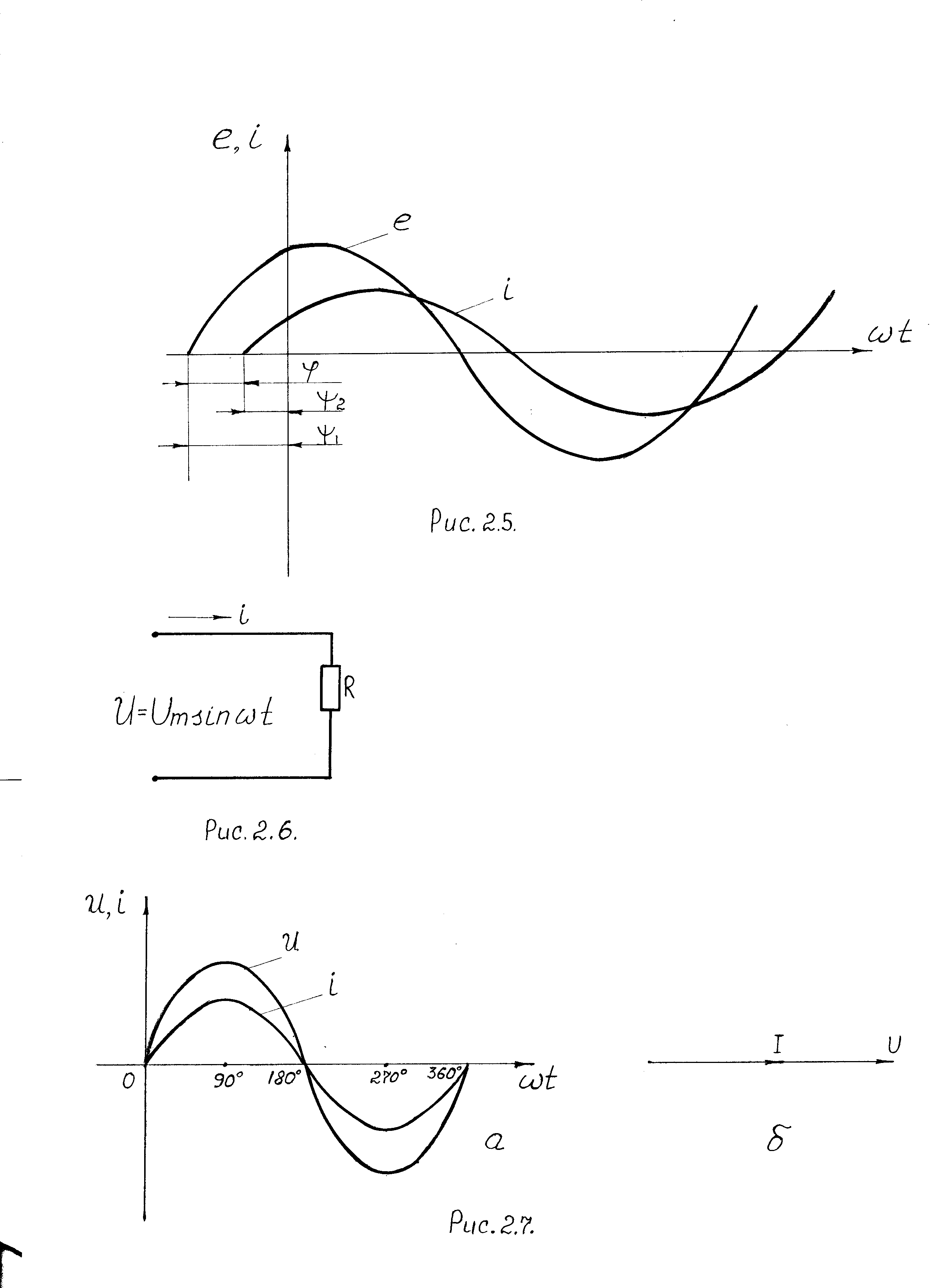
Рис. 2.7. Графики изменения напряжения и тока в цепи с активным сопротивлением (а); векторная диаграмма цепи (б)

Диаграмма, изображающая совокупность векторов, построенных с соблюдением их взаимной ориентации по фазе, называется векторной диаграммой.

2.6. Цепь переменного тока с идеальной катушкой индуктивности

Катушка индуктивности L включена в цепь синусоидального тока i = =I_msinωt (рис. 2.8). Катушка, у которой активное сопротивление R = 0 называется идеальной. Согласно второму закону Кирхгофа напряжение на входе цепи:

,

т.е. напряжение опережает ток на 90°, или ток отстает от напряжения на 90°, следовательно, индуктивность создает сдвиг по фазе.

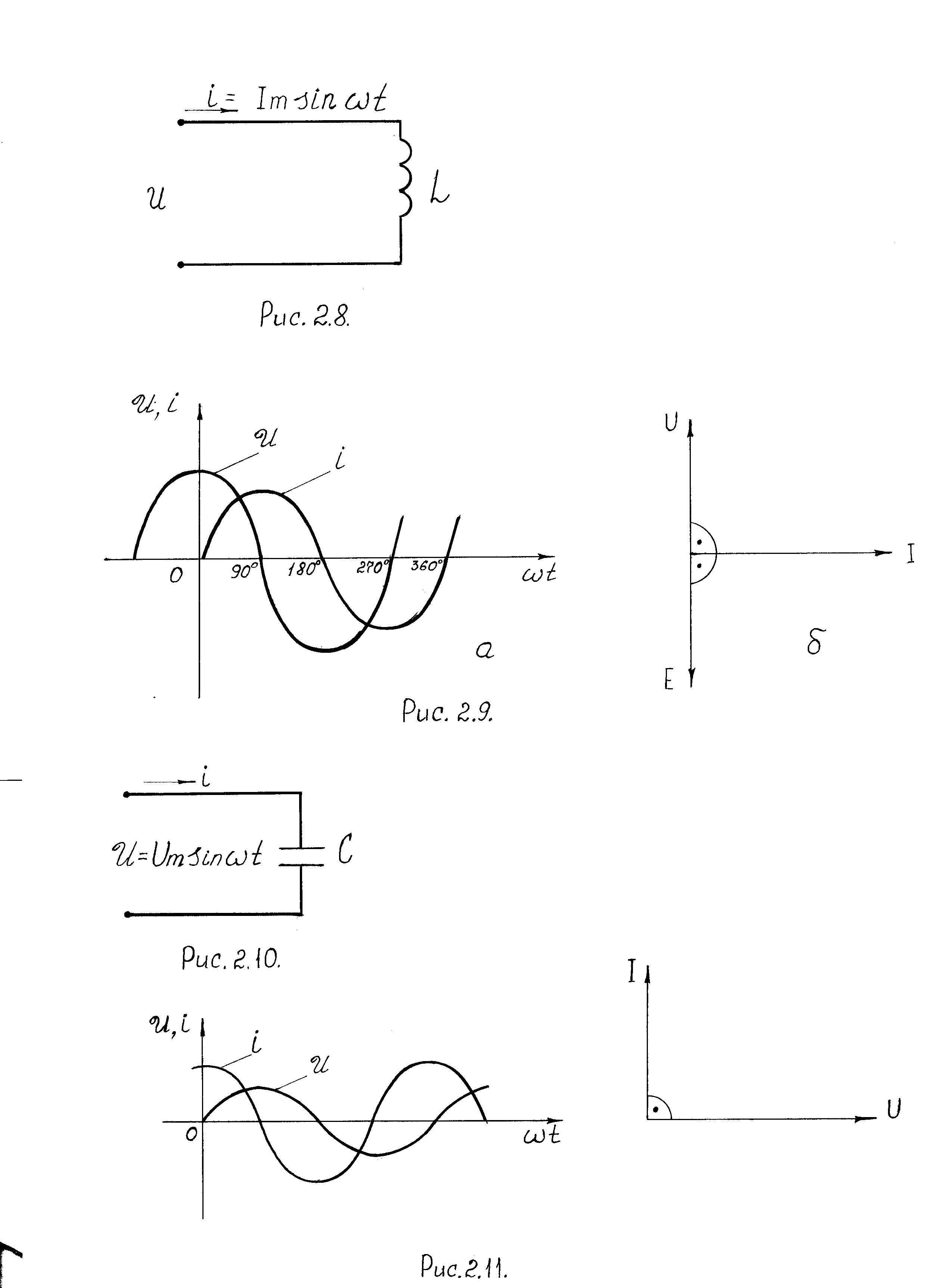
Рис. 2.8. Цепь переменного тока с индуктивной нагрузкой

Произведение ωL = 2πfL – индуктивное сопротивление, которое зависит от частоты питающего напряжения f и индуктивности L.

На рис. 2.9 представлены графики изменения напряжения и тока в катушке индуктивности, векторная диаграмма цепи.

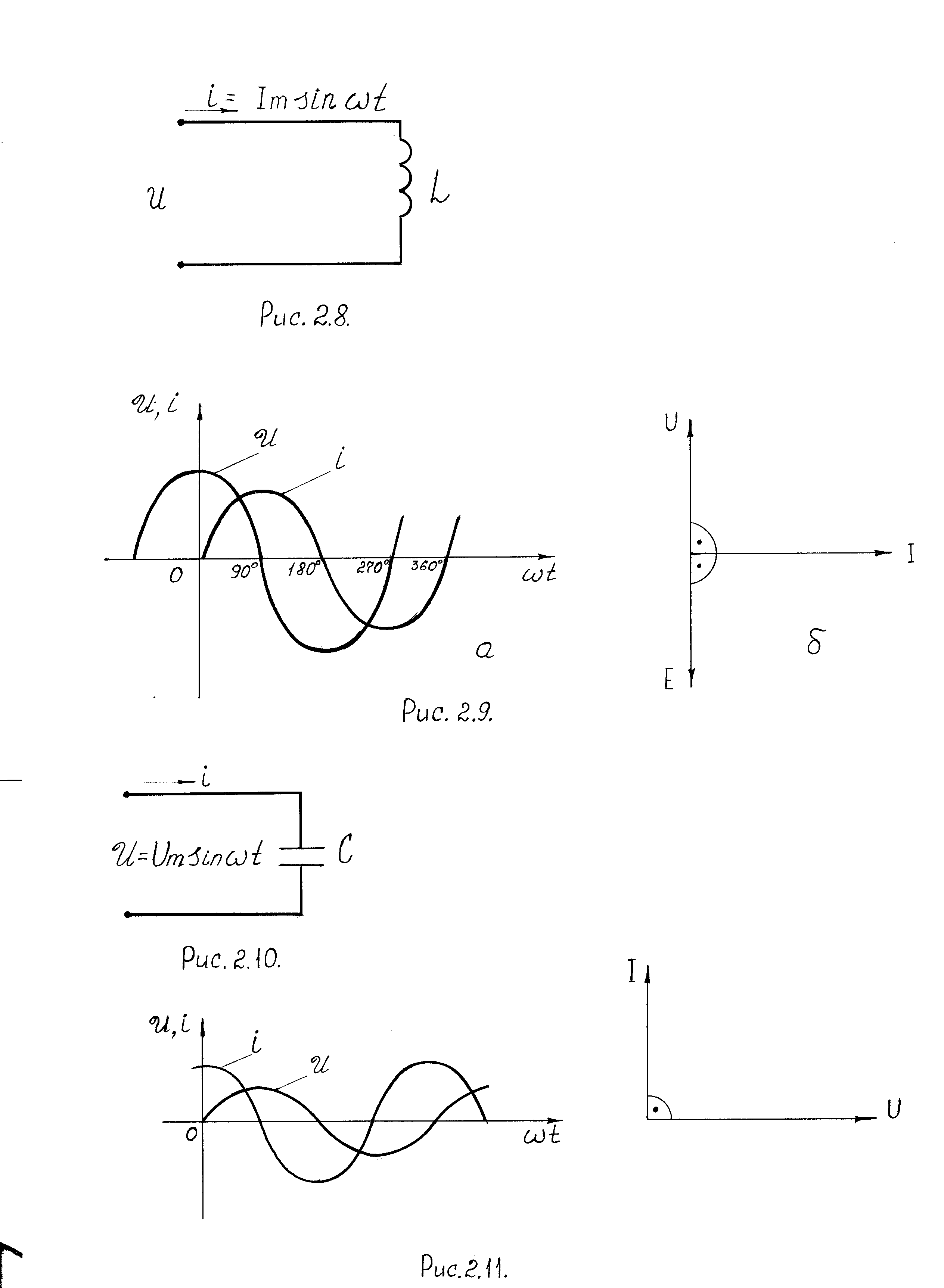
Рис. 2.9. Графики изменения напряжения и тока в цепи с идеальной катушкой индуктивности (а); векторная диаграмма цепи (б)

2.7. Цепь переменного тока с идеальным конденсатором

Конденсатор С включен в цепь с напряжением U = U_msinωt (рис. 2.10). Конденсатор, у которого активное сопротивление R = 0, называется идеальным.

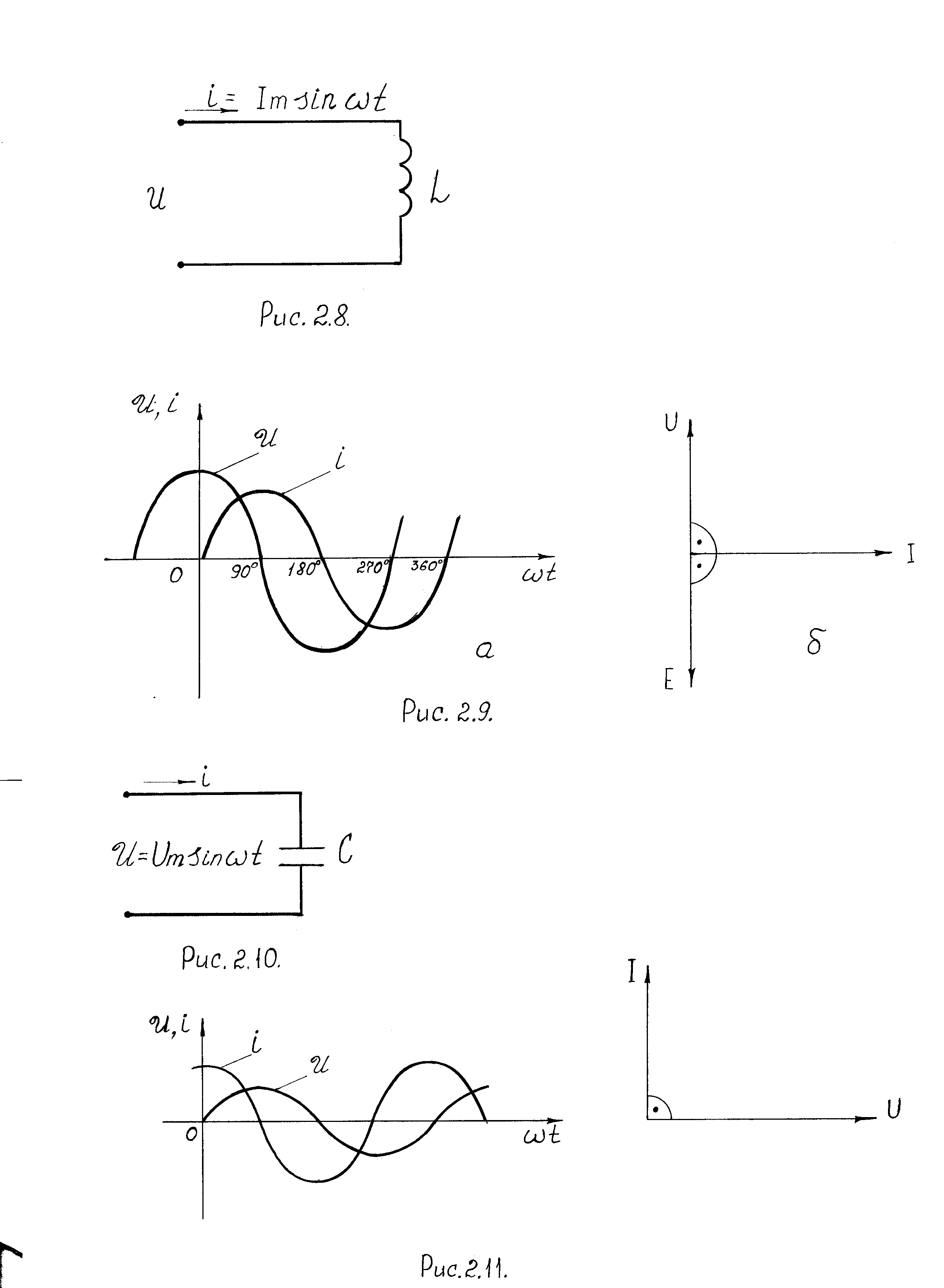
Рис. 2.10. Цепь переменного тока с емкостной нагрузкой

Если напряжение на конденсаторе изменяется по синусоидальному закону, то по синусоидальному закону изменяется и заряд конденсатора:

q = C·U = CU_msinωt.

Ток, протекающий через конденсатор:

,

т.е. ток через конденсатор опережает по фазе напряжение на угол 90°.

Величину называют емкостным сопротивлением, которое обратно пропорционально частоте питающего напряжения и емкости конденсатора.

На рис. 2.11 представлены графики изменения напряжения и тока в конденсаторе, векторная диаграмма цепи.

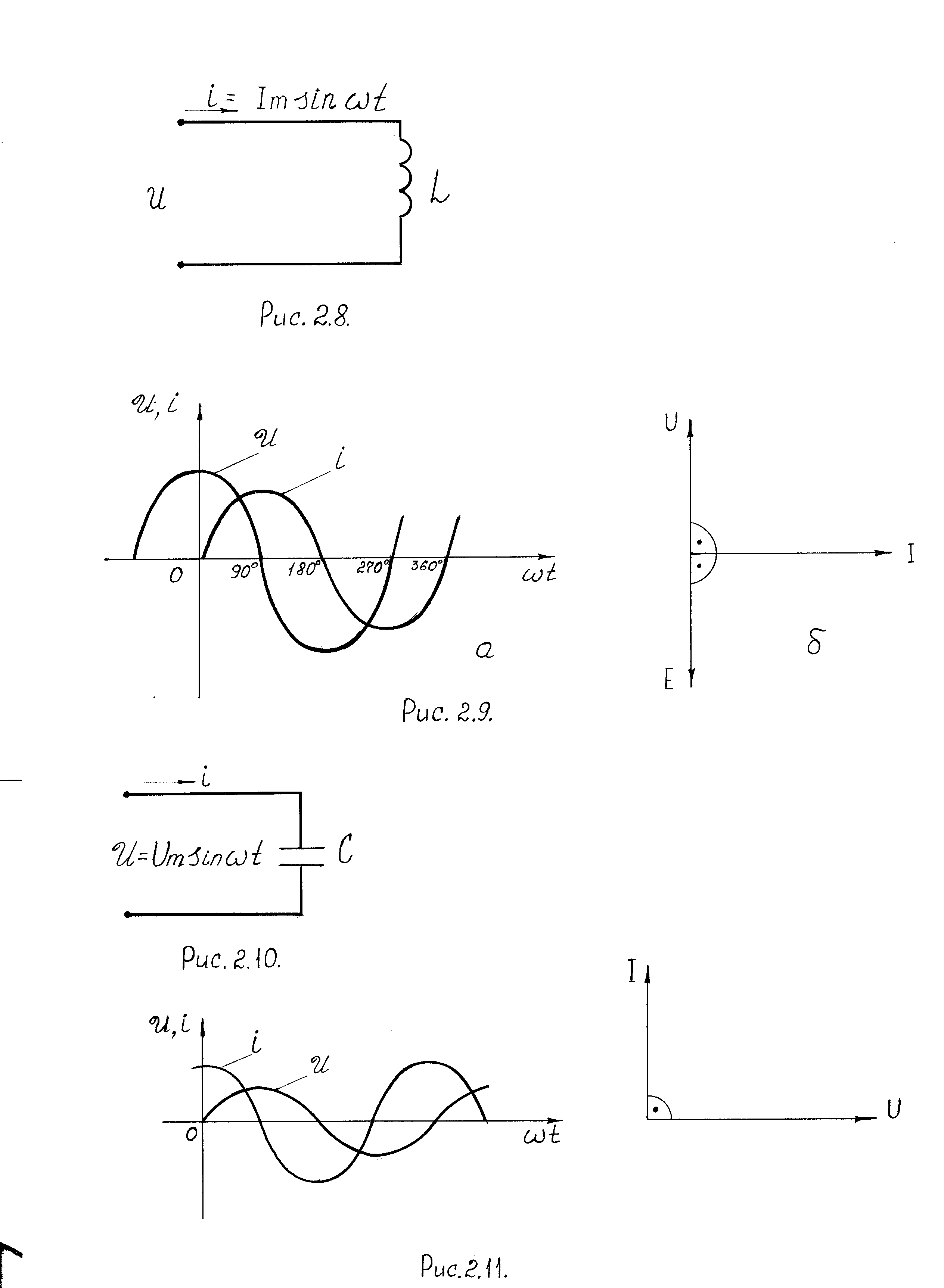
а б

Рис. 2.11. Графики изменения напряжения и тока в цепи с идеальным конденсатором (а); векторная диаграмма цепи (б)