2.11. Закон Ома в комплексной форме записи

Комплексное сопротивление Z включено в цепь переменного тока с напряжением (рис. 2.18). Точка над буквой Z не ставится, точку принято ставить над комплексными величинами, которые представляют синусоидальные функции времени.

Ток в цепи определяется по закону Ома:

,

где: R – активное сопротивление цепи;

X – реактивное сопротивление цепи, которое может быть индуктивным или емкостным;

z – модуль комплексного сопротивления;

φ – угол сдвига по фазе.

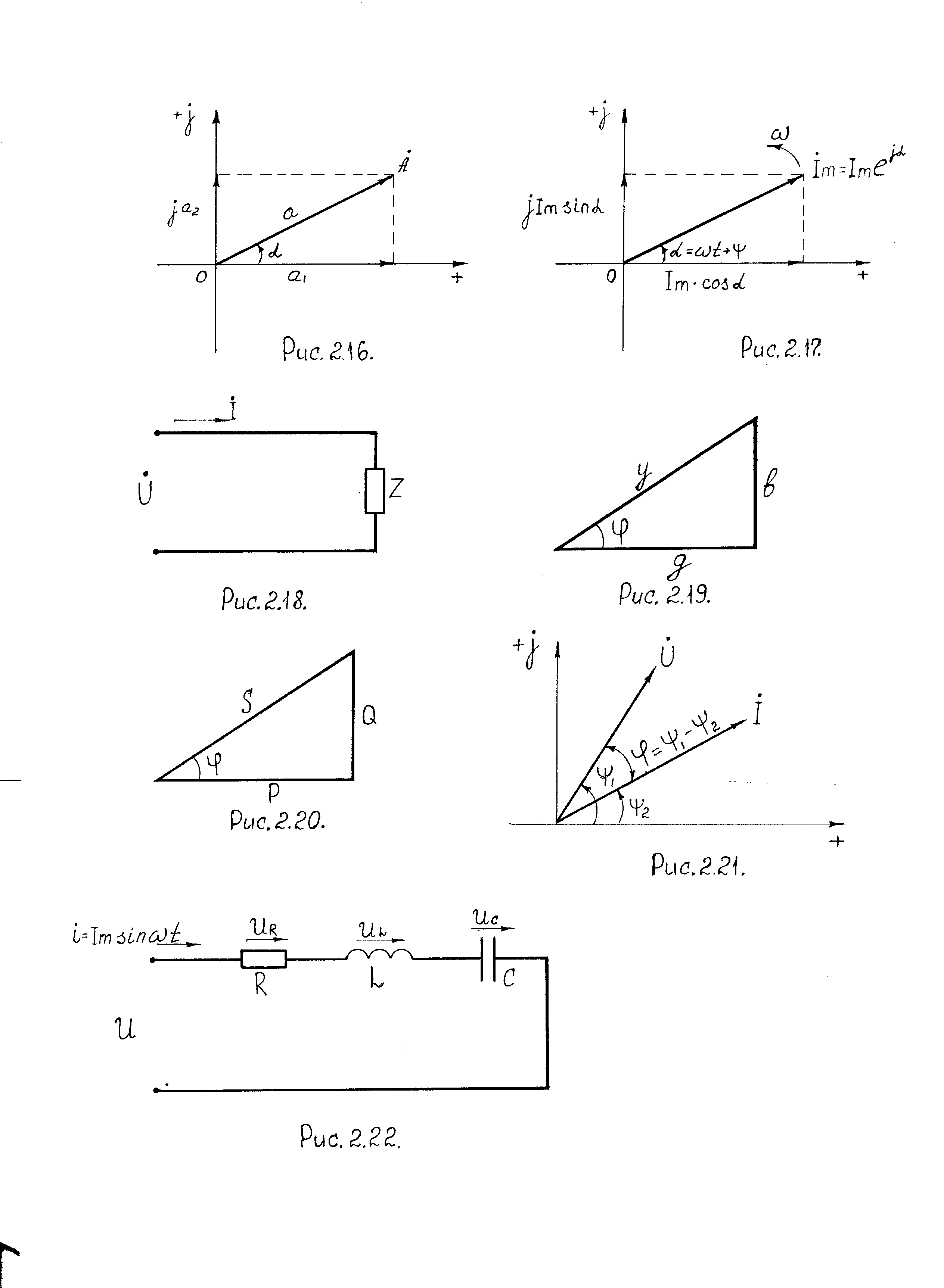
Рис. 2.18. Цепь переменного тока с комплексным сопротивлением Z

2.12. Комплексная проводимость

Под комплексной проводимостью Y понимают величину, обратную комплексному сопротивлению Z:

,

где: – активная проводимость;

–реактивная проводимость цепи.

Если X положительно, то и b положительно, при отрицательном X, b также отрицательно.

Аналогично треугольнику сопротивлений строим треугольник проводимостей (рис. 2.19). Треугольник проводимостей – графическая интерпретация связи между модулем полной проводимости у и ее активной и реактивной составляющими: .

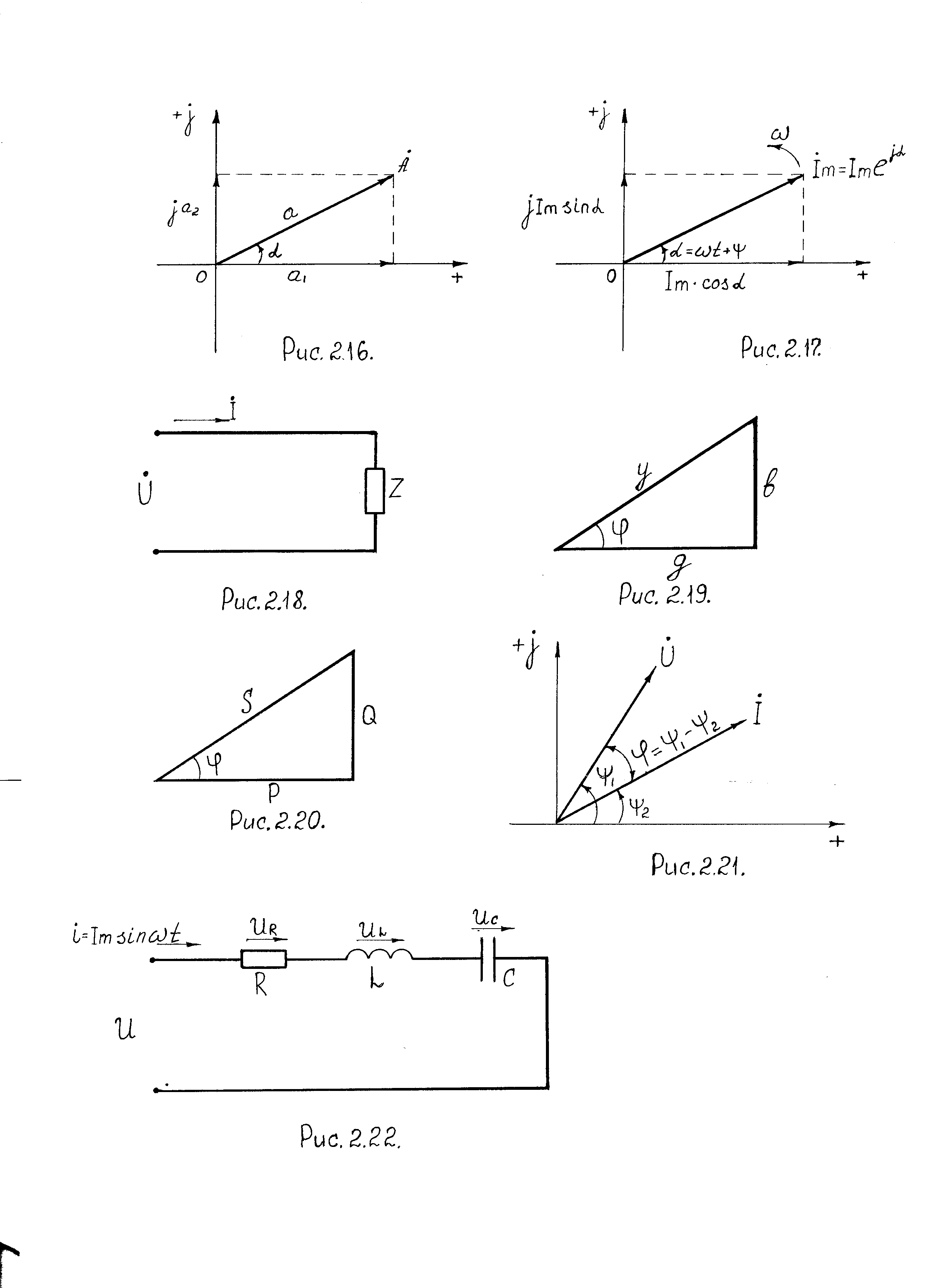
Рис. 2.19. Треугольник проводимостей

При использовании комплексной проводимости закон Ома записывается следующим образом:

=∙.

2.13. Активная, реактивная и полная мощность цепи переменного тока

Под активной мощностью Р понимают среднее значение мгновенной мощности р за период Т:

,

где: и = U_msin(ωt + φ) ; i = I_msinωt.

Активная мощность – это энергия, которая определяется в единицу времени (предполагается, что в 1 секунду укладывается целое число периодов Т) в резисторе R:

P = I²R [Вт].

Реактивная мощность Q = UIsinφ [вар].

Если sinφ > 0, то и Q > 0, если sinφ < 0, то Q < 0.

Полная мощность определяется из треугольника мощностей (рис. 2.20), который подобен треугольнику сопротивлений:

или S = U·I [В·А].

Рис.2.20. Треугольник мощностей

Из треугольника мощностей получаем:

.

2.14. Комплексная форма записи мощности

Допустим, что к электрической цепи (см. рис. 2.18) подведено напряжение , по цепи протекает ток . Представим эти два вектора на комплексной плоскости (рис. 2.21).

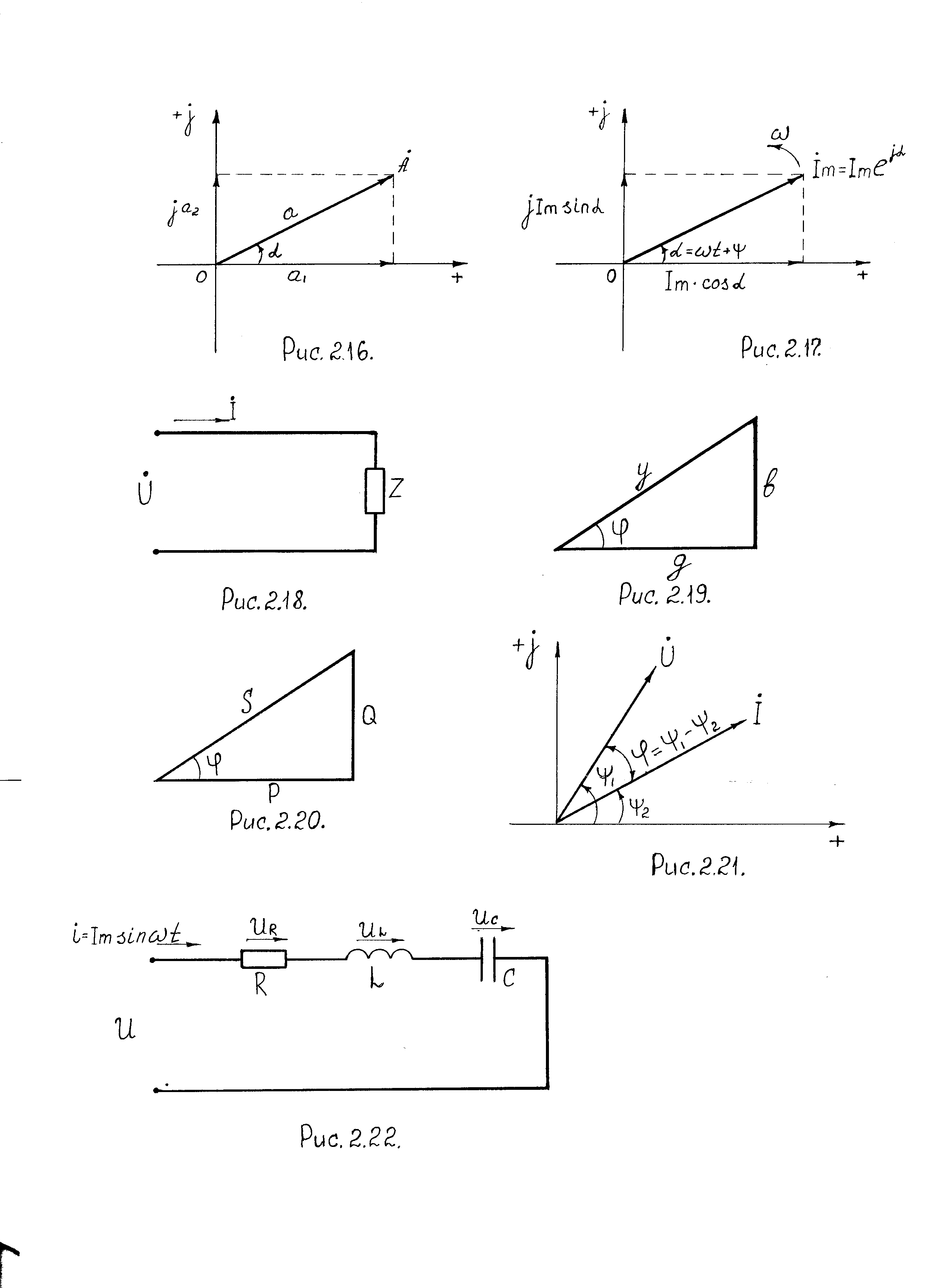
Рис. 2.21. Комплексные напряжение и ток

Комплексная мощность

,

где: – сопряженный комплекс тока;

s – модуль комплексной мощности.

2.15. Законы Кирхгофа в комплексной форме записи.

Для цепей переменного тока справедливы законы Кирхгофа, сформулированные ранее для цепей постоянного тока, см. 1.5, п. 1.6.

Согласно первому закону сумма комплексных токов в узле равна нулю:

.

Второй закон применяется к любому замкнутому контуру цепи:

,

где:

–алгебраическая сумма комплексных э.д.с. источников напряжения;

–падения напряжений на комплексных сопротивлениях Z_k отдельных участков.

2.16. Цепь переменного тока с последовательным соединением элементов

Согласно второму закону Кирхгофа для цепи рис. 2.22 можно записать

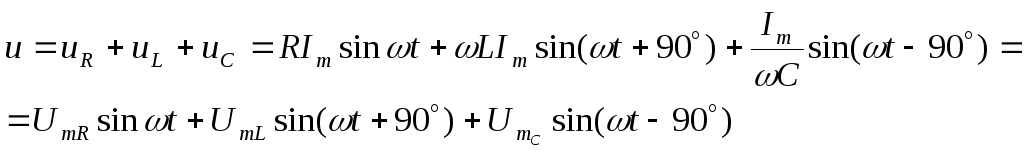
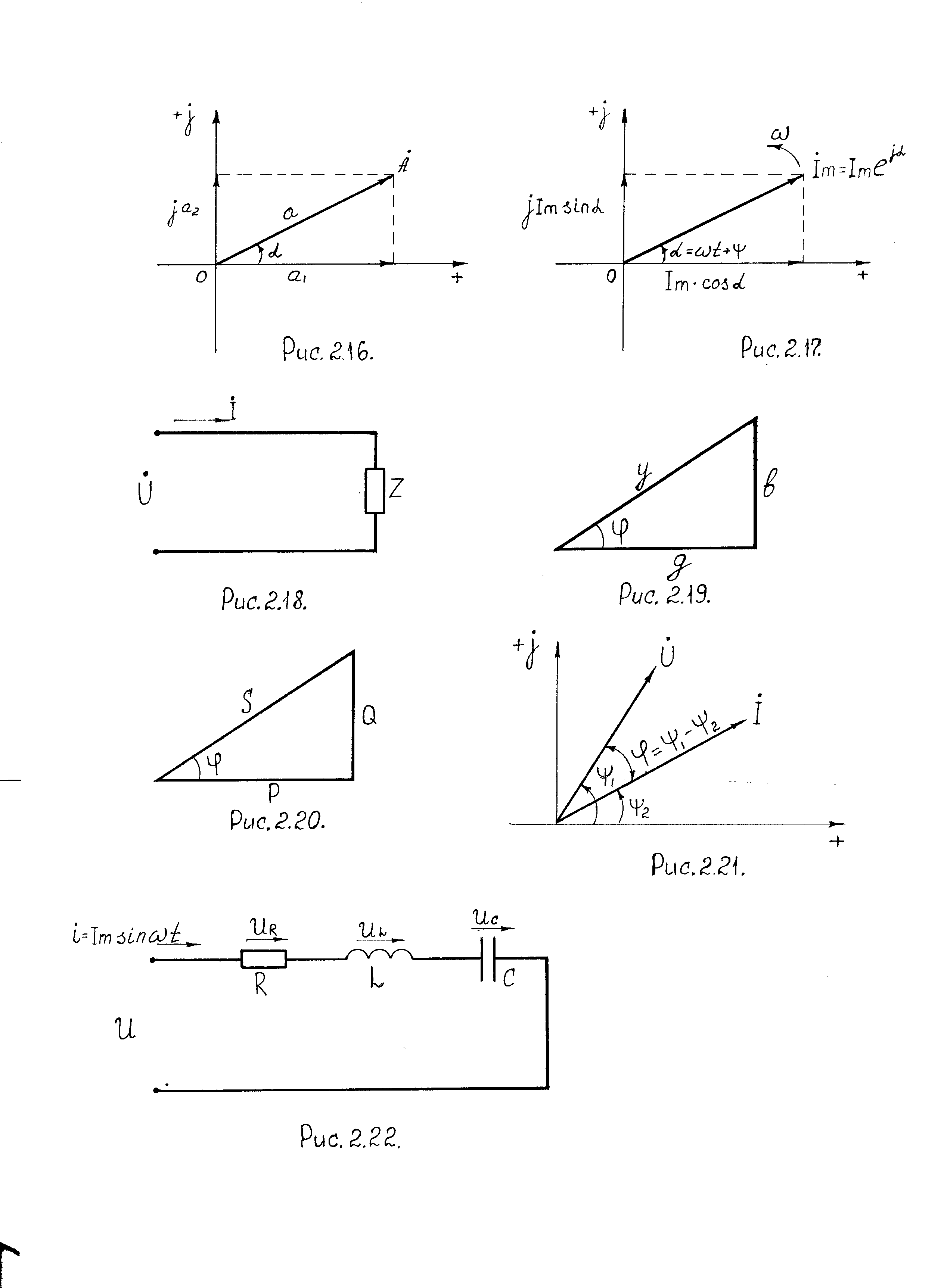
Рис. 2.22. Цепь переменного тока с последовательным соединением R, L, С

Для действующих значений

,

где: X_L – X_C = X – реактивное сопротивление цепи.

Ток в цепи определяется по закону Ома:

или в комплексной форме записи:

,

где: – напряжение, приложенное к цепи;

Z – комплексное сопротивление цепи.

В данной цепи возможны следующие три варианта.

1. Индуктивное сопротивление больше емкостного X_L > Х_C , следовательно, U_L > U_C .

Векторная диаграмма для этого случая представлена на рис. 2.23, а. Вектор для наглядности изображен рядом с вектором, в действительности компенсирует . Угол в данном случае положительный, вектор напряжения опережает вектор тока на угол φ.

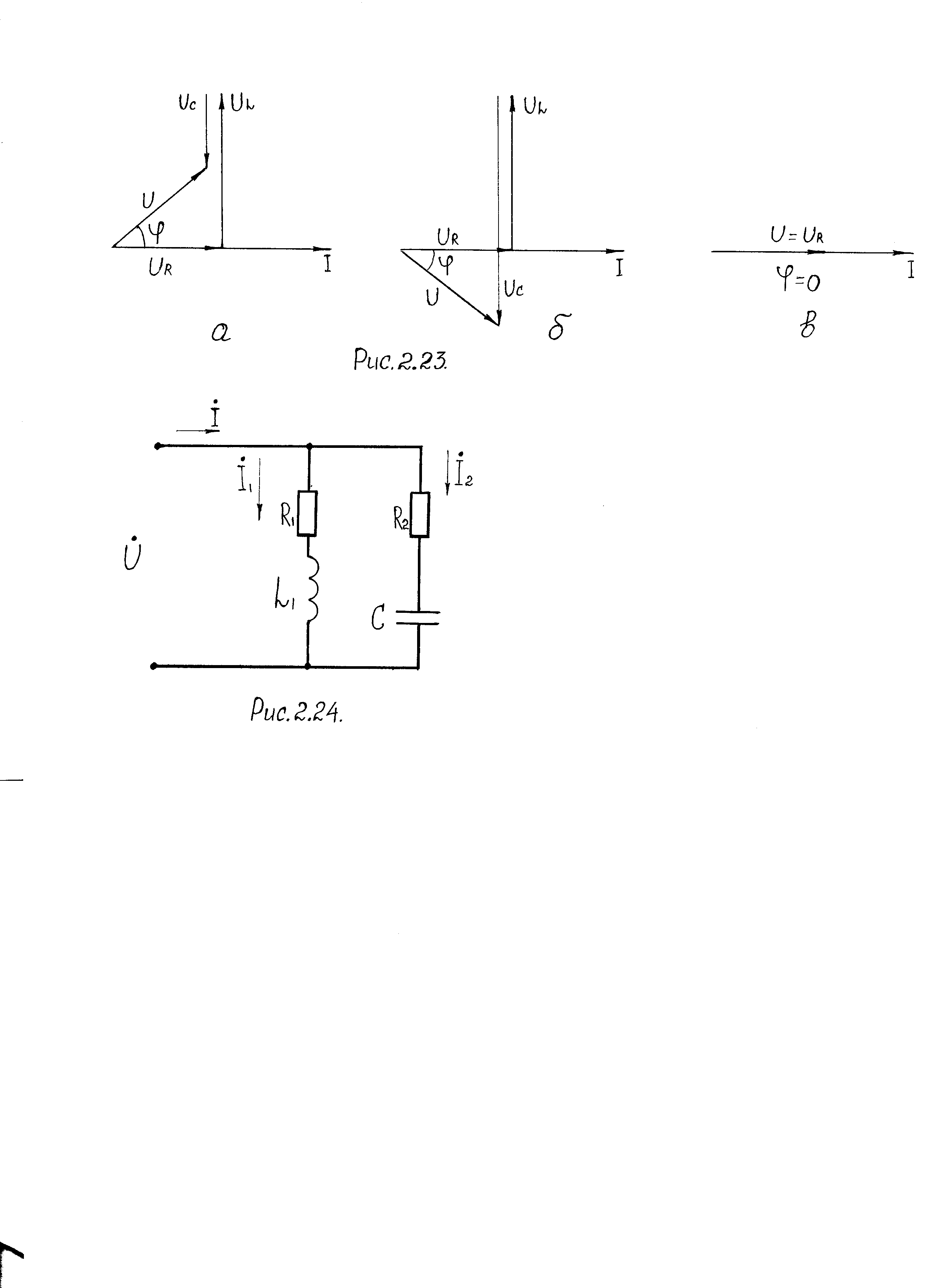
Рис. 2.23. Векторные диаграммы для цепи с последовательным соединением

R, L, C: a – X_L > X_C ; б – X_L < X_C ; в – X_L = X_C

2. Индуктивное сопротивление меньше емкостного Х_L < Х_C, следовательно, U_L < U_c (рис. 2.23, б), угол φ отрицательный, вектор тока опережает вектор напряжения на угол φ, по отношению к сети нагрузка является активно-емкостной.

3. Индуктивное сопротивление равно емкостному X_L = Х_с – условие резонанса напряжений (рис. 2.23, в).

Реактивное сопротивление цепи X = X_L – Х_с = 0, полное сопротивление равно активному Z = R. Ток в цепи определяется величиной активного сопротивления и намного превышает номинальное значение тока для данной цепи. Напряжения на реактивных элементах равны U_L= X_L I = U_C = Х_с I и превышают в раз напряжение сети U=U_R. Угол сдвига фаз φ = 0, следовательно, cosφ = 1.

Активная мощность цепи равна полной Р = UIcosφ = UI = S, а реактивная Q = UIsinφ = 0.

Резонансная частота последовательного колебательного контура зависит от величины индуктивностиL и емкости С.

Явление резонанса напряжений широко используют в различных электрорадиотехнических устройствах.