Синтез законов управления на основе эталонных мм, заданных в операторной форме.
Основная операторная
форма ММ – ПФ. Можно срисовать ПФ с
желаемой ЛАЧХ и получить ПФ ЗС:
.
Но ПФ скорее всего окажется слишком
сложной, поэтому корни числителя и
знаменателя необходимо проанализировать
и максимально упростить ПФ ЗС. Можно
подправить неустойчивые корни, сократить
близкие постоянные времени (например
69 и 73), но порядок системы должен быть
больше порядка объекта и разность
порядков полиномов числителя и знаменателя
также должна быть больше порядка объекта.
Затем можно построить эту систему вClassic,
оптимизировать
ее.
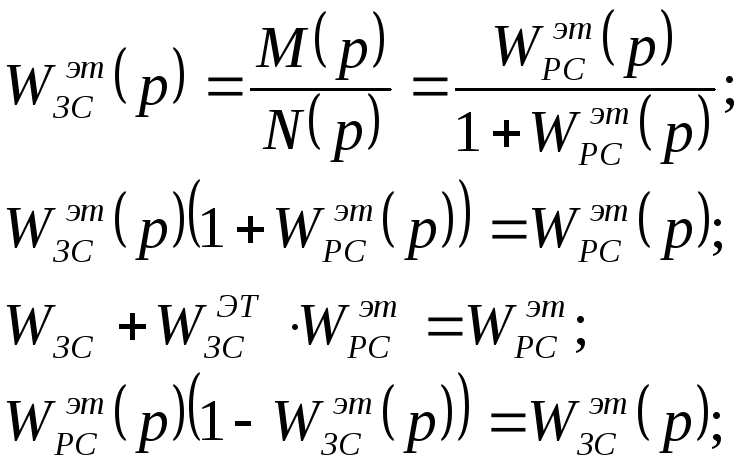
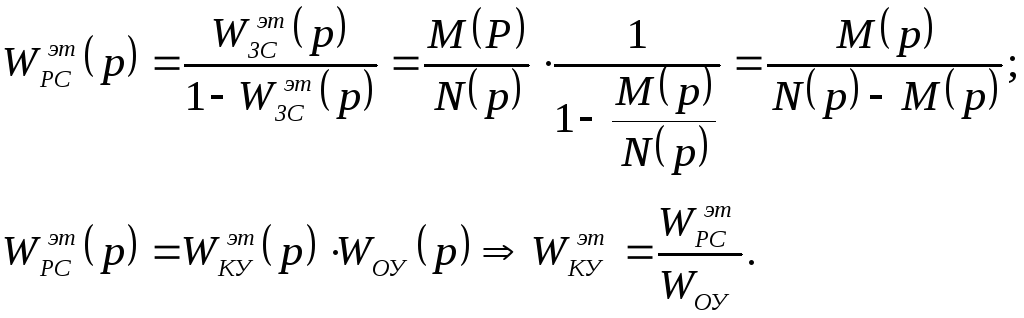
Методика построения эталонных операторных мм на основе типовых пп.
Эталонные ММ удобно строить в нормированном виде, то есть в такой форме описания динамических и статических свойств проектируемой системы, когда зависимые и независимые переменные модели являются величинами безразмерными. Тогда синтезу подлежит только форма ПП, а конкретный вид ММ определяется под каждую конкретную задачу путем масштабирования зависимых и независимых переменных.
Переход к любой реальной модели; находим связь реальной зависимой переменной с нормированной и связь независимой переменной с нормируемой величиной.
Такое свойство наблюдается для систем любого порядка.
Если есть похожие
ПП, различающиеся
,
их можно записать в унифицированном
виде ММ, которая потом может быть
транспонирована под любой масштаб
физических величин и
.
Нормирование
позволяет унифицировать процедуру
синтеза эталонных ММ, а следовательно
строить ММ, задающие только динамику
проектируемой системы с унифицированными
числами, характеризующими эту динамику.
Если нормирование применяется к
одномерным физическим объектам (то есть
с одной выходной переменной), то
нормирование ММ этого объекта или
системы можно осуществлять и по амплитуде,
и по
.
Нормирование по
амплитуде: в последовательно -
структурированной форме
берем равным 1.
Нормирование по времени:
Нормирование по
времени всегда осуществляется
применительно к левой части уравнения
(то есть к ХП). Поделим уравнение на
:
В этом уравнении
Способов нормирования
по времени может быть много, самый
распространенный
.
То есть необходимо привести уравнение
к виду:
.
;
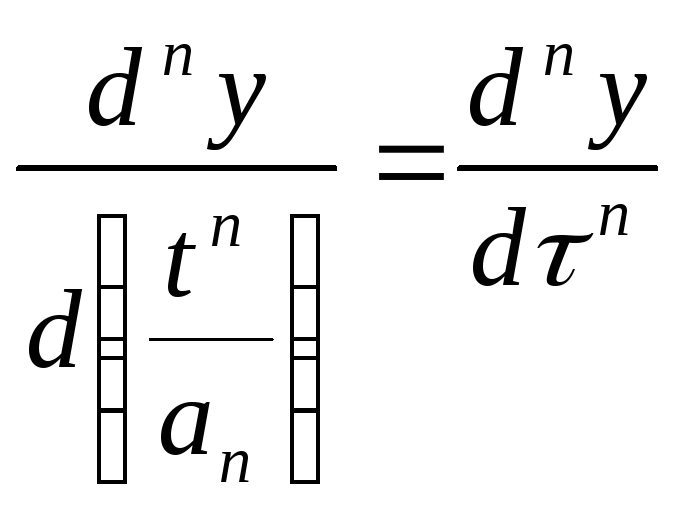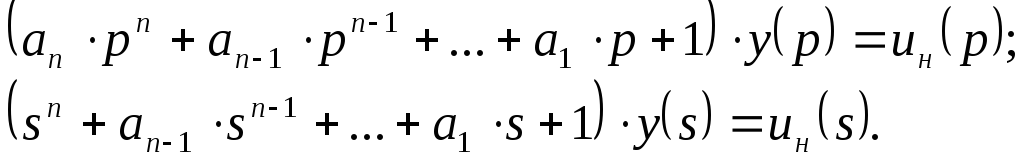
- комплексная
переменная.
,
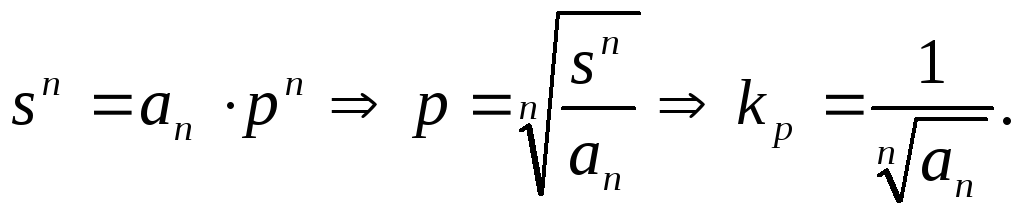
где
- задано,
- на графике.
Рисунок 34.
Для нормирования
полинома:
.
(все корни
одинаковые).
Рассмотренная процедура и описанная в пособии касается только первого этапа синтеза эталонной ММ – синтеза полинома эталонной ММ. После разнормирования этот эталонный ХП будет иметь не единственный коэффициент при старшей степени и единичный свободный член. Таким образом мы получаем знаменатель ПФ:
Таким образом,
чтобы, к примеру, получить систему с
астатизмом первого порядка, необходимо,
чтобы полином числителя также имел
свободный член, следовательно, при
вычитании
получим астатизм первого порядка.
Синтез зу по эталонным дифференциально-временным мм.
В основу метода
отождествления высших производных
положен тот факт, что выходной сигнал
проектируемой системы тождественно
совпадает с выходным сигналом ОУ. Другими
словами, это один и тот же сигнал,
следовательно, если есть ММ ОУ и эталонная
ММ проектируемой системы, выходы которых
обозначены как
и
,
то имеет место тождество:
Следовательно,
если ММ ОУ и проектируемой системы имеет
такую форму, что их можно разрешить
относительно высшей производной, то
,
где
- дифференциальный оператор.
;
Тогда, если
имеет такую форму, которая разрешается
относительно
,
то из этого уравнения можно выразить
,
то есть получить закон управления.
ЭММ проектируемой
системы в данном методе может быть
построена любым способом. Например,
любым из двух, рассмотренных выше, так
как если есть ПФ, то можно записать
соответствующее ей дифференциальное
уравнение. По сути используемых
преобразований метод позволяет
синтезировать системы с произвольным
порядком астатизма. Для этого, как и для
ПФ, необходимо соблюдать условие:
коэффициент при соответствующих
производных в правой и левой частях
уравнения должны быть равны. Если
коэффициенты при производных выходных
сигналов в левой части обозначить
,
а коэффициенты при производных входных
сигналов через
,
то необходимо для достижения требуемого
астатизма соблюдать условия:
для первого порядка
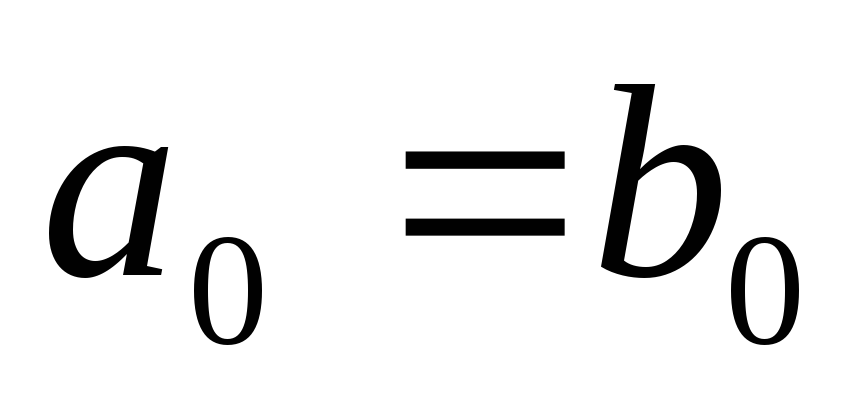;для второго порядка
Однако, в отличие от операторного метода, который при соблюдении указанных условий обеспечивает реальный астатизм системы, в данном методе реализуется псевдоастатизм, так как ЗУ формируется непоследовательным преобразованием входного сигнала, а через аддитивное сопоставление операторов, процедура которого в общем случае некорректна.