8.Многогранники и кривые поверхности.

Общее понятие о многогранниках и кривых плоскостях

Многогранником называют тело, поверхность которого состоит из взаимно пересекающихся плоскостей.

Основными элементами всякого многогранника являются: грани, ребра и вершины

( рис. 57).

Из многогранников наибольшее распространение получили пирамиды и призмы.

Пирамида – многогранник, боковые грани и ребра которого пересекаются в одной точке, называемой вершиной.

Призма – многогранник, боковые грани и ребра которого перпендикулярны к пл.σ, называемой пл. нормального сечения, или боковые ребра которого параллельны между собой.

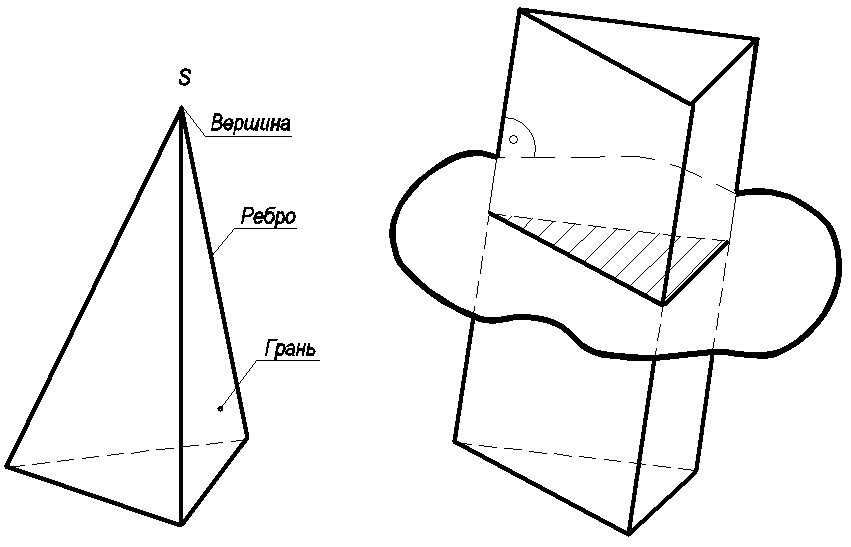
Рис. 57 Рис. 58

Если точка находится на пов. многогранника, то ее проекции следует искать на проекциях прямой, проходящей через эту точку в соответствующей грани многогранника (рис.58).

Кривой поверхностью называется поверхность, образованная при движении прямой или кривой линии в пространстве по определенному закону. (cм. рис. 59).

Линия, производящая поверхность наз. образующей.

Линия, по которой движется образующая называется направляющей.

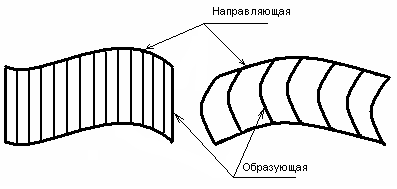
Рис. 59

Поверхности разделяются на линейчатые – образующая прямая линия и нелинейчатые - образующая кривая линия.

Из линейчатых поверхностей получили наибольшее распространение цилиндрические и конические поверхности, из нелинейчатых поверхности вращения.

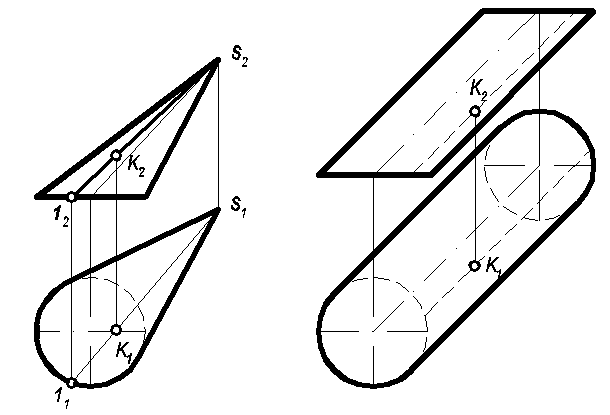
Рис. 60

Если точка находится на поверхности тела, то ее проекции следует искать на проекциях линии (образующей), при­надлежащей поверхности данного тела.(см. рис. 60).

Особую группу кривых поверхностей составляют поверхности вращения, полученные при вращении образующей вокруг какой – либо оси(рис. 61).

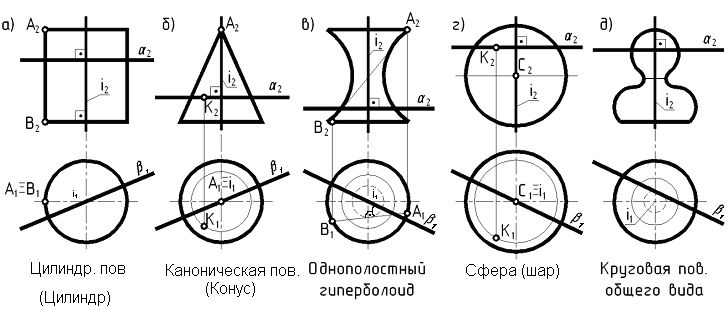
Рис. 61

При сечении пов. вращения плоскостью (α) ┴ оси вращения в сечении получается окружность - параллель. Наименьшая параллель наз. горлом, наибольшая - экватором.

При сечении поверхности вращения плоскостью (β), проходящей через ось i в сечении получается фигура, называемая меридианом. Меридиан, параллельный пл. П₂ наз. главным.

9.Кривые линии

Кривые линии широко применяются в машиностроении, архитектуре, в строительстве и других областях науки и техники.

Кривую линию можно рассматривать как непрерывную совокупность последовательных положений движущейся точки , а также как линию пересечения поверхностей или поверхности с плоскостью.

Кривые линии могут быть плоскими, если все точки их лежат в одной плоскости.

Например: окружность, эллипс, парабола, гипербола.

Кривые линии называются пространственными, если они не лежат всеми своими точками в плоскости.

Например: винтовые линии.

Кривые линии - плоские и пространственные (двойной кривизны) – делятся на математические (аналитические или трансцендентные) и графические (определяемые только их изображениями).

Степень уравнения, которое описывает алгебраическую кривую (окружность, эллипс и т.д.) определяет порядок кривой. Геометрический порядок плоской кривой определяется числом точек пересечения с прямой линией. Порядок пространственной кривой определяется числом точек пересечения кривой с плоскостью.

Свойства проекций кривой : 1) в общем случае проекции кривой линии являются так же кривыми линиями; 2) если точка принадлежит кривой линии , то её проекция принадлежит одноимённым проекции этой кривой; 3) касательная к кривой линии проецируется в касательную к проекции этой линии.

Плоские кривые получили широкое распространение. Для исследования локальных

свойств плоской кривой строят в некоторой точке касательную и нормаль.

Касательной к плоской кривой (t) в некоторой точке(А) называется предельное положение секущей, когда две общие точки сечения, стремясь друг к другу совпадают.(рис. 62 а.).

Н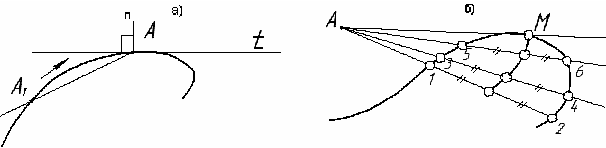ормальюназывается прямая лежащая в плоскости кривой и перпендикулярная касательной в точке (А) её касания (рис. 62 а.)

При решении некоторых задач приходится проводить касательную (t) к кривой из некоторой точки (А) с помощью “кривой ошибок” (рис. 62 б.). Применение этого метода основано на том, что в точке касания (М) кривизна равна нулю. Через точку (А) проводят пучок прямых пересекающих кривую. Полученные хорды делят пополам. Плавная кривая, проведённая через средние точки (“кривая ошибок”),пересекает заданную кривую в точке касания (М).

Рис. 62

Свойства точек кривой:

Рис. 63

Т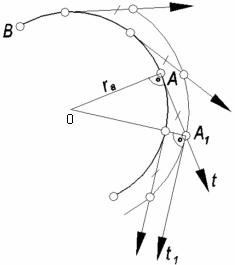очка кривой, в которой можно провести единственную касательную, называетсягладкой. Кривая состоящая только из таких точек называется гладкой. Точка кривой называется обыкновенной, если при ее движении по кривой направление её движения и направление поворота касательной не изменяется. Точки не удовлетворяющие этим условиям называются особыми.

На рис. 63 изображены особые точки кривой: точка перегиба А – касательная пересекает кривую; точка возврата В; точка возврата второго рода С; точка излома Д- кривая в этой точке имеет две касательные.

Рис. 64

Понятие о кривизне.

Кривизной (К) плоской кривой в данной точке называется величина, обратная радиусу соприкасающейся окружности (К=1/r).

Например , кривизна прямой линии равна нулю, а кривизна окружности во всех ее точках величина постоянная. Кривизна других кривых в каждой точке различна. Она определяется с помощью окружности соприкасающейся в этой точке.

Соприкасающейся окружностью называется предельное положение окружности, когда она проходит через данную точку и две другие бесконечно близкие к ней точки. На риc. 64 показано построение центра и радиуса кривизны кривой линии ВС в заданной точке. На кривой по обе стороны от данной точки помечают несколько точек и проводят из них и из точки А полукасательные. На полукасательных откладывают произвольные, но равные отрезки и через полученные точки проводят кривую линию. Точке А заданной кривой соответствует точка A₁ построенной кривой. В пересечении нормалей , проведённых в точках А и A_{1 ,} получим О – центр кривизны и величину радиуса кривизны (r_a) в точке А(центр и радиус соприкасающейся окружности).

Проекции плоских кривых.

Важное прикладное значение имеют некоторые кривые второго порядка – эллипс, парабола, гипербола.

а) б) в)

Рис. 65

Эллипс(замкнутая кривая с двумя осями симметрии и центром) представляет собой геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек (фокусов) есть величина постоянная, равная большой оси(рис. 65 а.). Эллипс можно построить по точкам исходя из этого описания. Из точки С радиусом а проводят дугу , которая пересекает большую ось эллипса в точках F₁ и F₂ . Затем из этих точек проводят дуги окружностей r и 2a-r. Точки пересечения дуг принадлежат кривой эллипса (например точка М) . Уравнение эллипса

Парабола (незамкнутая кривая с одной осью симметрии) представляет собой геометрическое место точек, равноудалённых от заданной точки (фокуса) и прямой (рис. 65 б.). параболу можно построить по точкам исходя из её определения, если задан фокус F и прямая ON- директриса. Вершина А делит пополам расстояние между фокусом и директрисой. Уравнение параболы Y²=2*p*x .

Гипербола (кривая, состоящая из двух ветвей, с двумя осями симметрии и центром) представляет собой геометрическое место точек, разность расстояний от которых до двух заданных точек (фокусов) есть величина постоянная(рис. 65 в.). Две прямые линии, проходящие через центр О и касающиеся гиперболы в бесконечно удалённых точках, называются асимптотами гиперболы. Асимптоты проведены по диагоналям прямоугольника со сторонами 2а и 2в. Гиперболу, как и параболу, можно построить по точкам.

Уравнение гиперболы

Пространственные кривые линии

Для пространственной кривой судить о характере её точек можно только при наличии двух проекций. Широкое применение в практике получили цилиндрические и конические винтовые линии. Рассмотрим одну из них.

Цилиндрическая винтовая линия представляет собой кривую линию одинакового уклона. Эта траектория описывается в пространстве точкой, равномерно перемещающейся вдоль образующей цилиндра , которая одновременно равномерно вращается вокруг оси цилиндра. (рис. 66).

На рисунке 66 представлена проекция цилиндрической винтовой линии. Окружность основания цилиндра (диаметром d) и шаг n разделены на одинаковое число частей (n=8). Так как ось цилиндра перпендикулярна к плоскости П₁ , то горизонтальная проекция винтовой линии сливается с окружностью представляющую горизонтальную проекцию поверхности цилиндра. Фронтальная проекция винтовой линии ясна из построения, она подобна синусоиде.

Развёртка витка цилиндрической винтовой линии показана на рис. 66. В развёрнутом виде каждый виток представляет собой отрезок прямой с углом падения φ, который можно определить по формуле tg φ = h/πd, где h –шаг винтовой линии , а d– диаметр цилиндра.

Винтовая линия может быть левой или правой. Если на видимой(передней) стороне цилиндра подъём проекции винтовой линии слева направо – это правая винтовая линия; если справа на лево - то левая винтовая линия.

Е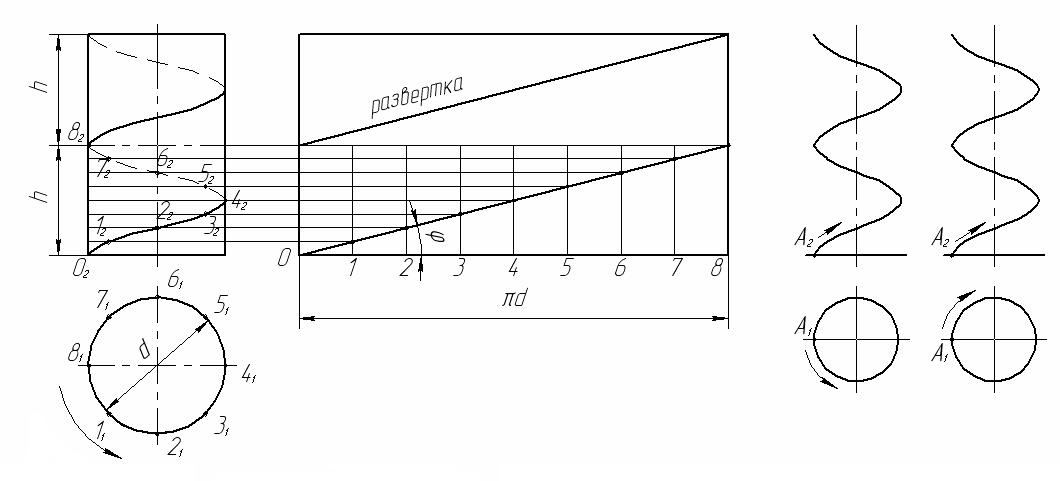сли винтовая линия изображена без цилиндра и без проекции точек, то указание о том, является ли она правой или левой, надо делать или надписью или стрелками, как показано на рис.67а.- для правой и рис. 67б. – для левой.

а) б)

Рис. 66 Рис. 67