7. Способы преобразования комплексного чертежа.

Проецируемые предметы в пространстве располагаются, как правило, в общем положении по отношению к пл.проек­ций, что затрудняет решение целого ряда задач, особенно, связанных с измерениями различных элементов. Поэтому производят преобразование комплексного чертежа так, чтобы новое изображение предмета (или системы) соответ­ствовало его частному положению, при котором упрощается решение пространственной задачи.

Преобразование комплексного чертежа может производит­ся двумя способами:

1. Изменением положения плоскостей проекций при неизменном положении предметов в пространстве (метод перемены плоскостей проекций).

2. Изменением положения предметов в пространстве при неизменном положении плоскостей проекций (методы: плоско-парал­лельного перемещения, вращение вокруг проецирующей прямой, вращение вокруг линии уровня и др.).

Метод перемены плоскостей проекций.

Сущность метода перемены пл. проекций заключается в том, что, положение предметов в пространстве остается неизменным, а система пл.проекций (П₁-П₂) последователь­но заменяется новой системой взаимно-перпендикулярных пл.проекций. При этом каждая новая плоскость проекций берется перпендикулярно к одной из оставшихся плоскостей проекций старой системы и соответствующим образом ориентируется в пространстве относительно системы предметов.

В зависимости от сложности задачи производится замена одной или обеих плоскостей проекций исходной системы (П₁-П₂).

Замена одной плоскости проекций.

П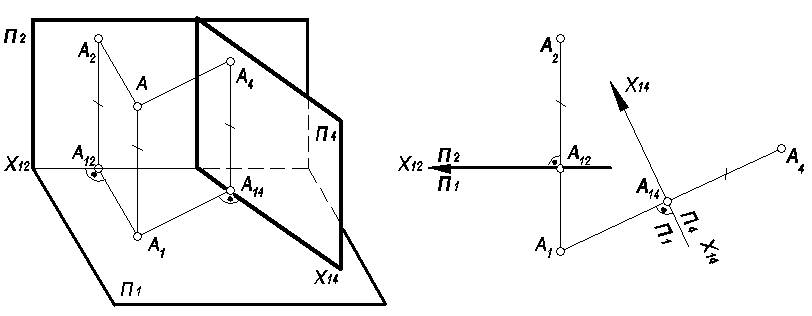ри замене одной плоскости проекций (П₂) на новую (П₄), перпендикулярную к одной из оставшихся плоскостей проекций (П₁), расстояние новой проекции точки (А₄) от новой оси (Х₁₄) равно расстоянию заменяемой проекции точки (А₂) от заменяемой оси (Х₁₂), т.е. А₄А₁₄=А₂А₁₂ (рис. 44)

Рис. 44

Пример 1: Определить натуральную величину отрезка прямой (рис. 45).

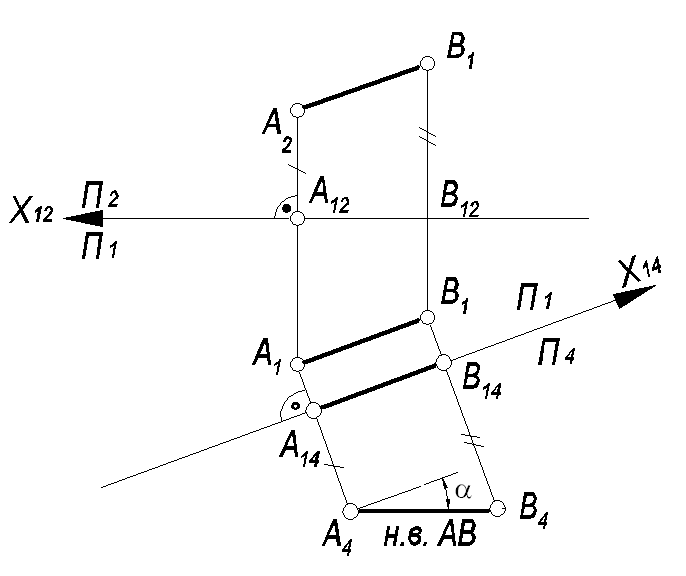
Заменяем плоскость П₂ на плоскость П₄ .При этом П₄ ┴ П_{1 .}

Плоскость П₄ берем параллельно АВ в пространстве. При этом на чер­теже новая ось X₁₄ //A₁B₁. Через точки А₁ и B₁ проводим прямые, перпендикулярные Х₁₄ и отклады­ваем отрезки A₄A₁₄=A₂A₁₂, B₄B₁₄=B₂В₁₂. Отрезок А₄В₄=АВ, т.к. АВ стала линией уровня – фронталью относительно пл.П₄.

Рис. 45

Пример2: Преобразовать пл. (∆АВС) в горизонтально-про­ецирующую (рис.46)

В ∆АВС проводим фронталь f . Заменяем плоскость П₁ на новую П₅ ┴ П₂. При этом П₅ берется перпенди­кулярной f в пространстве. На чертеже новая ось проекций X_{2. 5} ┴ f₂. На пл. П₅ АВС проеци­руется в линию В₅А₅С₅.

Рис. 46

Замена двух плоскостей проекций.

Замена обеих плоскостей проекций исходной системы производится последовательно по правилу замены одной пл.проекций, которое применяется дважды.

П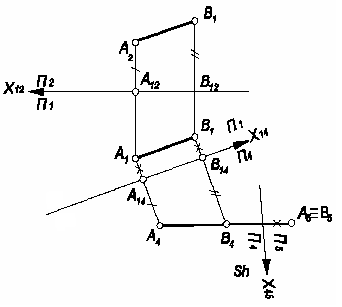ример 1: Преобразовать отрезок прямой общего положения АВ в горизонтально- проецирующую прямую. Заменой пл.П₂ на пл. П₄ преоб­разуем АВ во фронталь. При этом ось X₁₄ //A₁B₁. Второй заменой пл. П₁ на пл. П₅ преобразуем АВ в горизонтально - проеци­рующую прямую. При этом ось Х₄₅ ┴ А₄В₄.

На пл. П₅ АВ проецируется в (·) А₅≡В₅ (рис. 47).

Рис. 47

Пример 2: Определить натуральную величину ABC, рас­положенного в плоскости общего поло­жения.

В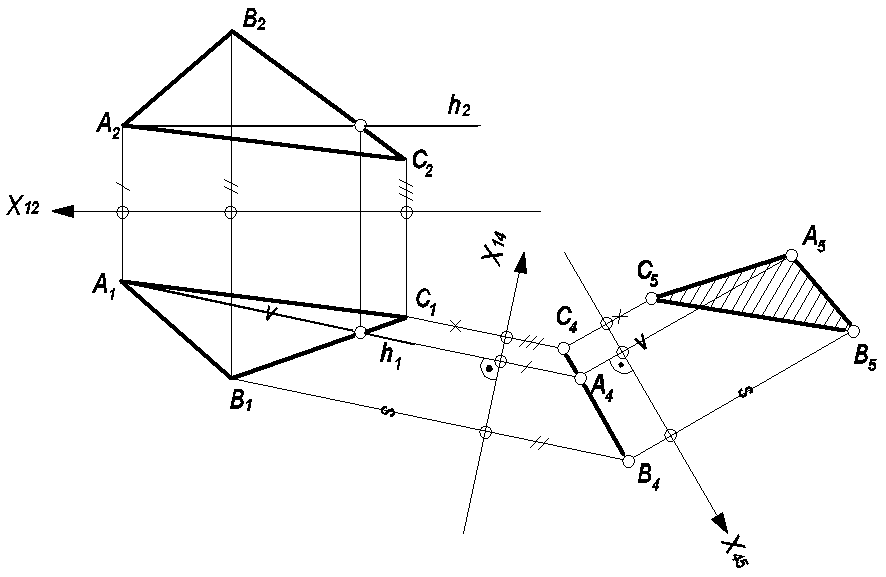∆ABC проводим горизонталь h Заменяем пл. П₂ на пл. П₄ ┴ П₁. Пл.П₄ ┴ пл. ∆ABC (┴h ). На чертеже ось X₁₄ ┴ h₁. На плоскость П₄ ∆АВС проецируется в линию С₄А₄В₄. Заменяем пл.П₁ на пл.П₅ ┴ П₄. Пл. П₅ // пл. ∆АВС. На чертеже ось Х₄₅ // С₄А₄В₄. На пл. П₅ ∆ABC проецируется в натуральную величину, т.е.

∆А₅В₅С₅ = ∆ABC (рис. 48).

Рис. 48

Метод плоско-параллельного перемещения.

Плоско-параллельным называется такое перемещение фигуры в пространстве, при котором все точки ее пере­мещаются в плоскостях, параллельных между собой.

Если фигура в пространстве совершает плоско-параллельное перемещение относительно какой-либо плоскости проекций (например, П₁); то проекция фигуры на эту плоскость проек­ций перемещается, оставаясь равной самой себе (плавающая проекция); на другой плоскости проекций (П₂) при этом все точки проекций фигуры перемещаются по прямым, парал­лельным оси проекций (X₁₂).

В зависимости от сложности задачи плоско-параллельное перемещение производится относительно одной или последо­вательно относительно двух плоскостей проекций.

Пример 1: Прямую AВ преобразовать в горизонтально-проеци­рующую прямую.

Плоско-параллельным перемещением относительно пл. П₁ преобразуем АВ во фронталь, При этом новая горизонтальная проекция прямой A’₁ B’₁= A₁B₁ располагается параллельно оси Х₁₂ На фронтальной проекции точки А₂ и В₂ перемещаются по прямым параллельным X₁₂ и займут положение А’₂В’₂

(См. рис. 49).

Рис. 49

Плоско-параллельным перемещением относительно пл. П₂ преобразуем АВ в гор.- проец. прямую. При этом новая фр.проекция пря­мой А’’₂В’’₂ располагается перпендикулярно X₁₂. На плоскость П₁ прямая проецируется в (·) А₁`` ≡ В<sub>1</sub>``.

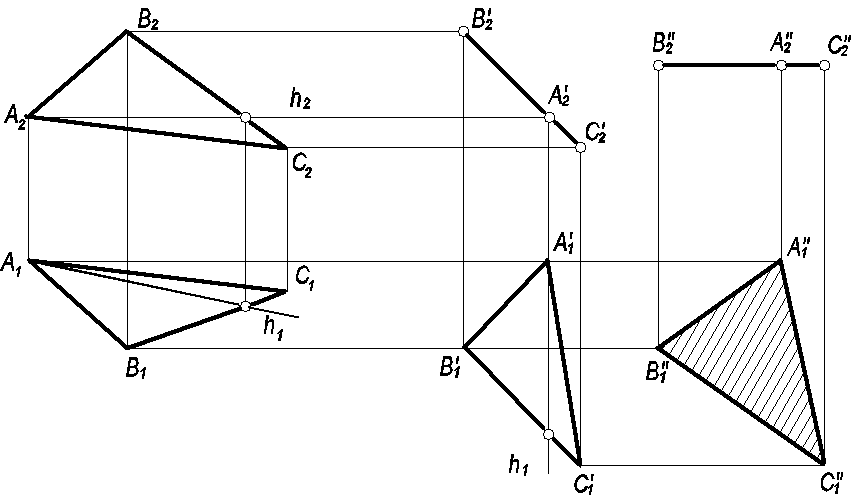Пример 2: Определить натуральную величину ∆ABC (рис. 50).

В ABC проводим горизонталь h . Плоско – параллельным перемеще­нием относительно пл. П₁ преобразуем ∆ABC во фр.-проецирующую плоскость. При этом в новом положении гор. проекция ∆А₁В₁С₁ = ∆А’₁В’₁С’₁ располагается так, что h₁ ┴ X₁₂. На пл. П₂ ∆ABC проецирует­ся в линию C’₂A’₂В’₂ Плоско – параллельным перемещением относи­тельно пл. П₂

Рис. 50

преобразуем ∆АВС в гор .плоскость уровня. При этом фр.проекция С’’₂А’’₂В’’₂ = С’₂А’₂В’₂ располагается параллельно оси Х₁₂.

На пл. П₁ ∆ABC проецируется в натуральную величину ∆А’’₁В’’₁С’’₁.

П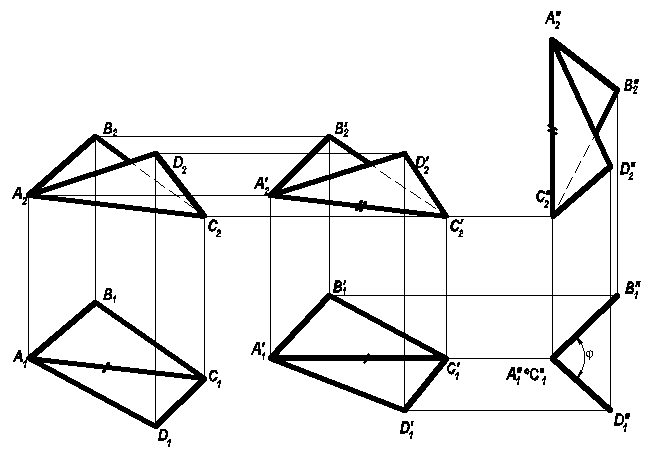ример 3: Определить истинную величину двугранного угла АВСD при ребре AC(рис.51).

Плоско-параллельным перемещением относительно пл. П₁ преобразуем ребро АС во фронталь. При этом в новом положении гор. проекции двухгранного угла А₁¹С₁¹ // X₁₂

Вторым плоско-параллельным перемещением относительно пл.П₂ преобразуем ребро АС в гор.- проецирующую прямую. При этом на фронтальной проекции двугранного угла A’’₂ C’’₂ ┴X₁₂. На горизонтальной проекции < В’’₁А’’₁D’’₁ = φ.

Рис. 51

Метод вращения вокруг проецирующей прямой.

При вращении фигуры вокруг оси, перпендикулярной к плоскости проекций (например: П₁) все точки этой фигуры в пространстве движутся по дугам окружности, центры которых находятся на оси вращения.

Н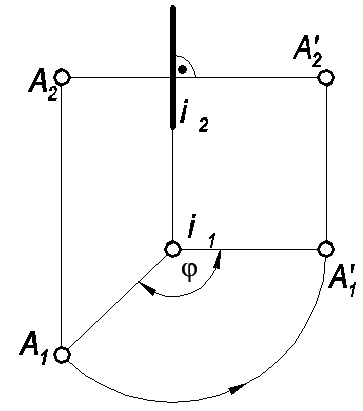а ту плоскость проекций (П₁) , которой перпендикулярна ось вращения, каждая дуга проецируется без искажения, на другую плоскость (П₂) в виде прямой параллельной оси проекций (Х₁₂) или перпендикулярной проекции оси вращения.

Пример 1: Повернуть точку А вокруг оси i на заданный

угол φ.

Так как ось i ┴ П₁, (·) А₁ повер­нется вокруг центра i₁ , на угол φ и займет положение (·) A’₁. На фронтальной проекции (·)А₂ перемещается по прямой перпендикулярной i₂ и займет положение (·) А’₂. (см. рис. 52).

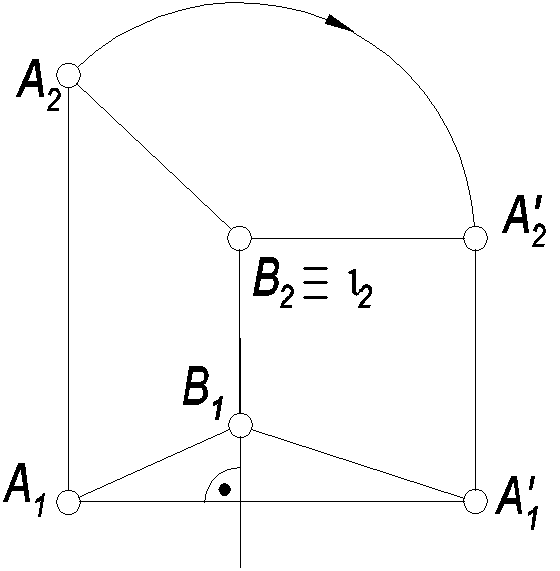
Рис. 52

Пример 2. Определить натуральную величину отрезка АВ.

Через (·)В проводим ось i ┴ П₂. Поворачиваем отрезок АВ вокруг оси до положения параллельного пл. П₁. При этом (·)А₂ повернется вокруг центра i₂ до положения (·)A’₂, при котором A’₂B₂ ║X₁₂ при этом (·)A₁ переместится по прямой A₁A’₁ ┴ i₁. Отрезок B₁A’₁ = AB т.к. АВ стала горизонталью.

Рис. 53

Пример 3: Определить расстояние от (·)D до плоскости ∆АВС.

В ∆АВС проводим горизонталь h . Через (·)А проводим ось 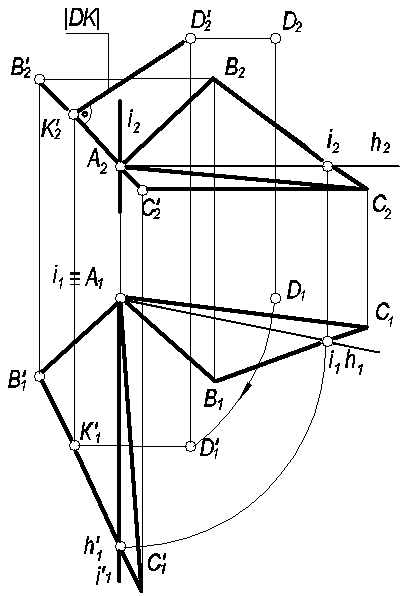i ┴ П₁. Поворачиваем систему вокруг оси i до положения, при кото­ром h ┴ П₂. При этом h₁ ┴ X₁₂ На пл.П₂ ∆ABC проецируется в линию В’₂А’₂С’₂. Перпенди­куляр D’₂K₂ , опущенный на линию В’₂А’₂С’₂ и есть расстояние от (·)D до пл. ∆АВС(cм. рис. 54).

Рис. 54

Метод вращения вокруг линии уровня.

Метод применяется для определения натуральной величины различных плоских фигур.

При вращении плоской фигуры вокруг линии уровня все точки этой фигуры в пространстве движутся по ду­гам окружности, центры которых находятся на оси вращения. На ту пл.проекций, которой параллельна линия уровня, эти дуги проецируются в виде прямых, перпенди­кулярных к проекции оси вращения. Поскольку поворот фигуры производится до положения параллельности плос­кости проекций, задача сводится к определению проекций и натуральной величины радиусов вращения отдельных точек плоской фигуры.

П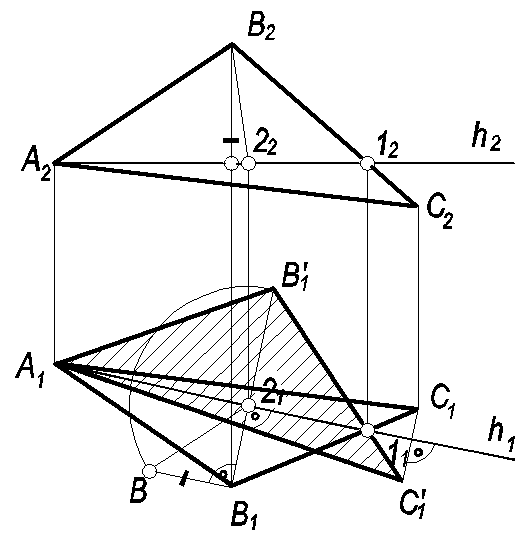ример 1 :

Определить натуральную величину ∆ABC (рис. 55).

В ∆ABC проводим линию уровня – горизонталь h. При вращении фигуры вокруг горизонтали точки В₁ и C₁ двигаются по прямым, перпендикулярным h₁. Определяем натуральную вели­чину радиуса вращения (·)В : R_B= В2₁, с помощью которого находим (·)B’₁, Проведя прямую В’₁1₁ до пересечения с гор. проекцией движения (·)С, находим (·)C’₁. ∆ А’₁B’₁С’₁ = ∆АВС, т.к. его плоскость параллельна пл. П₁.

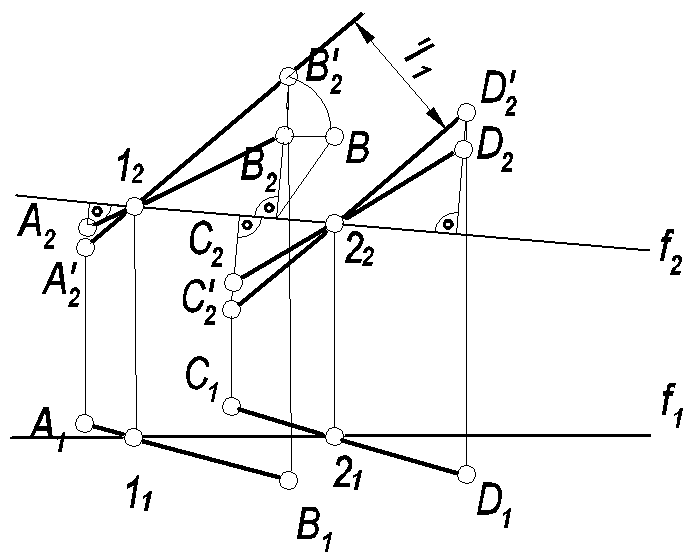
Рис. 55

Пример 2: Определить расстояние между двумя параллельными прямыми АВ и CD (рис. 56).

В пл.(АВ // СD) проводим фронталь f .

Определяем траектории движе­ния точек А,В,С и D на фр. пл. проекций. Находим натуральную величину радиуса вращения (.)В, и положение прямых A’₂B’₂ ║ C’₂D’₂, расстояние между которыми и есть искомая величина| l |.

Рис. 56