Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Донской государственный технический университет

(ДГТУ)

Кафедра «Графики и начертательной геометрии»

УЧЕБНОЕ ПОСОБИЕ

по курсу «Начертательная геометрия»

(для самостоятельной работы студентов всех форм обучения)

г. Ростов-на-Дону

2008 Г.

Составители:

доцент Соломин А.Н

проф. Савенков М.В.

доцент Ананченко А.И

УДК 514(015)

Методическое пособие составлено в помощь студентам всех форм обучения , изучающих курс начертательной геометрии.

Пособие содержит методические указания по изучению теоретической части курса в соответствии с существующей программой для технических ВУЗов. Методическое пособие следует рассматривать как дополнение к читаемым лекциям и рекомендуется использовать при самостоятельной подготовке к практическим занятиям по изучаемому курсу.

Печатается по разрешению методической комиссии конструкторского факультета

Научный редактор : д.т.н, профессор Кузин Г. А.

Рецензент : Зав. кафедрой “Графики” РГАСМ профессор Бородин Д.Н.

Введение Понятие о проецировании.

Начертательная геометрия – это теория изображения пространственных тел на плоскости или поверхности и решения пространственных задач с помощью этих изображений.

Предметом начертательной геометрии является:

1. Изложение способов построения изображений пространственных тел на плоскости (или поверхности);

2. Обоснование способов решения пространственных задач с помощью изображений;

3. Использование способов начертательной геометрии для решения различных задач науки и техники.

Основным средством начертательной геометрии является изображение или чертёж

(эпюр – фр.), к которому предъявляются определённые требования. Чертёж должен быть наглядным, обратимым, простым и достаточно точным.

Некоторые принятые обозначения:

Плоскости проекций: П_{1 ,} П_{2 ,} П₃ и т.д.

Точки: В пространстве: А, B, С, D и т.д.

В проекциях: A_{1 ,} B₁ ,C_1, D₁ …

A_2, B_2, C_2, D₂ …

A_3, B_3, C_3, D₃ …

Линии: в пространстве: a, b, c, d, e и т.д.

в проекциях: a₁ b₁ c₁ d₁ e_{1 …}

а₂ b₂ c₂ d₂ e_{2 …}

a₃ b₃ c₃ d₃ e_{3 …}

Плоскости: в пространстве: α, β, γ …

следами в плоскости: α₁ β₁ γ₁ …

α₂ β₂ γ₂ …

α₃ β₃ γ₃ …

Условные обозначения: Параллельность - ║

Перпендикулярность - ┴

Пересечение - ∩

Равенство - =

Совпадение - ≡

Принадлежность –()

Прямой угол -

Точка – ( • )

Основоположником начертательной геометрии является французский инженер и ученый Гаспар Монж (1748-1818), которому принадлежит крылатое выражение: "Чертеж - язык техника". Проф. В.К. Курдюмов (1853-1904), автор русского - классического учебника по начертательной геометрии писал: "Если чертеж является языком техника, то начертательная геометрия служит грамматикой этого языка..."

Изучение начертательной геометрии способствует раз­витию у обучающихся пространственного мышления, без ко­торого невозможно успешное выполнение различных инженерно-графических и проектно-конструкторских работ.

1. Понятие о проецировании

Проецирование это способ построения изображения или проекции пространственного тела. Проекцией геометрического тела называется правильно построенное изображение его на плоскости или поверхности вне тела, выполненное по опреде­ленным законам.

В зависимости от способа построения проекции делятся на центральные и параллельные.

Центральные проекции

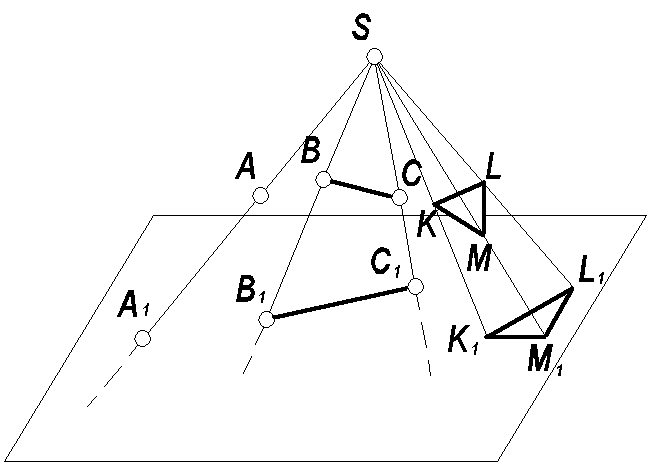
П₁- плоскость проекций;

S - центр проекций;

А - точка в пространстве;

SA - проецирующий луч;

А₁ - центральная проекция (·)А на плоскость П₁.

От центральной проекции точки А можно перейти к построению центральной проекции линии (ВС), фигуры (∆KLM) и тела, рассматривая их как совокупность точек в пространстве (рис. 1)

Центральные проекции получили

Рис. 1 распространение в архи­тектурно-строительном и

художественном деле.

Параллельные проекции

П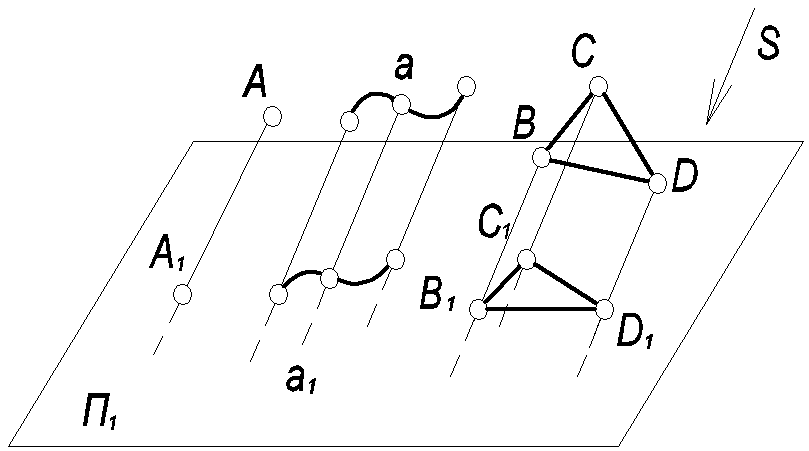араллельные проекции получаются, если центр проецирования S удален в бесконечность от плоскости про­екций П₁ . Тогда проецирующие лучи, становятся параллельными некоторому направлению проецирования S (рис. 2).

Для получения параллельной про­екции A₁ точки А достаточно прове­сти через нее луч АА₁ параллельный S до пересечения с плоскостью П₁.

Параллельные проекции линий (а), фигур (∆ВСD) и тел строят,

Рис. 2 рассматривая их как совокупность отдельных точек.

В зависимости от направления проецирования параллельные проекции делятся на прямоугольные и косоугольные. В первом случае - S ┴ П₁, во - втором S П₁.

Прямоугольные параллельные или ортогональные проекции нашли широкое применение в технике.

Основные свойства параллельного проецирования (рис. З).

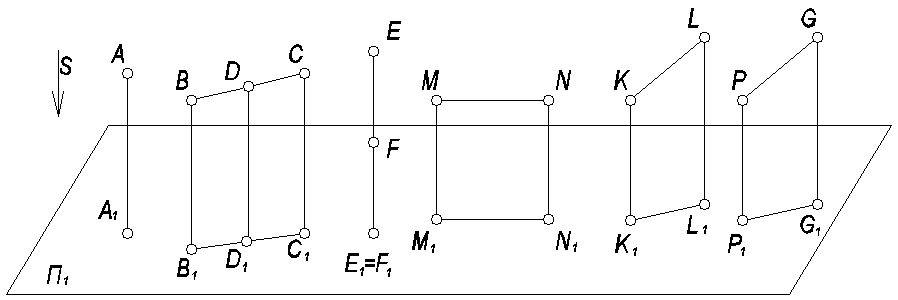
Рис. 3

1. Точка (А) проецируется на плоскость проекций в точку (A₁).

2. Прямая линия (ВС) в общем случае проецируется в прямую (B₁C₁), в частном случае - в точку (когда EF║S ) или в натуральную величину (когда MN║П₁).

3. Если точка (D) принадлежит прямой (ВС), то проекция этой точки (D₁) принадлежит проекции прямой (В₁С₁).

4. Отношение отрезков прямой равно отношению их проекций:

ВД ₌ В₁Д₁

ДС Д₁С₁

5.Проекции двух параллельных прямых (KL║PG) параллельны (K₁L₁║P₁G₁).

6. Отношение отрезков двух параллельных прямых, равно отношению их проекций:

KL ₌ K₁L₁.

PG P₁G₁