§3. Линейные дифференциальные уравнения и системы

Уравнение вида

,

где инепрерывные на промежуткефункции аргумента, называетсялинейным неоднородным дифференциальным уравнением (ЛНДУ) n-го порядка.

ТЕОРЕМА

Если на отрезке коэффициентыи правая частьуравнения непрерывны, то на всем этом отрезке существует, и притом единственное, решение дифференциального уравнения с начальными условиями,, … ,, где.

Если в данном уравнении , то уравнение называетсялинейным однородным дифференциальным уравнением (ЛОДУ) n-го порядка. Обозначим левую часть линейного дифференциального уравнения и назовемлинейным дифференциальным оператором n-го порядка.

Свойства линейного дифференциального оператора

. .

. .

Следствие. Из свойств и следует линейность оператора, то есть

Система из линейно независимых (лнз) на промежуткерешенийдля лодУn-го порядка называется фундаментальной системой решений (фср) этого уравнения.

ТЕОРЕМА

Пусть функции являются решениями ЛОДУn-го порядка с непрерывными коэффициентами. Тогда для того, чтобы системабыла линейно независима на, необходимо и достаточно, чтобыопределитель Вронского

для любого .

Типовой пример

Исследовать на линейную зависимость систему функций .

►Составим определитель Вронского:

.

Следовательно, система функций – линейно независима. ◄

Типовой пример

Исследовать на линейную зависимость следующую систему функций

.

►Составим определитель Вронского:

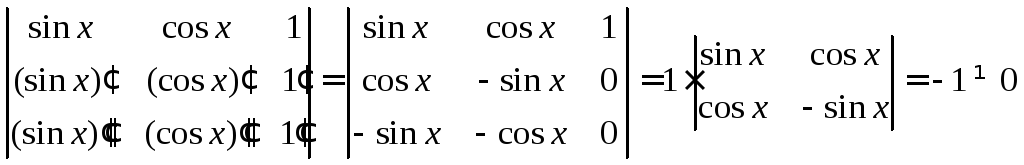
Следовательно, система функций - линейно независима. ◄

Типовой пример

Исследовать на линейную зависимость систему функций .

►Аналогично, для любого.

Следовательно, система функций – линейно независима. ◄

Таким образом, определитель Вронского играет определяющую роль в выяснении линейной зависимости системы функций.

Если определитель Вронского построен на частных решениях дифференциального уравнения, то справедливаформула Лиувилля – Остроградского

,

где – первый коэффициент дифференциального уравнения.

Для линейного однородного дифференциального уравнения второго порядка фундаментальная система состоит из двух линейно независимых решений; его общее решение находится по формуле.

Если для такого уравнения известно одно частное решение , то второе его решение,линейно независимое с первым, можно найти по формуле, являющейся следствием формулы Лиувилля – Остроградского:

.

Типовой пример

Найти общее решение дифференциального уравнения , проверив, что одно его частное решение имеет вид.

►Разделим обе части данного уравнения на :

.

Здесь коэффициенты инепрерывны при, следовательно, решение дифференциального уравнения существует в области. Подставляя, получим тождество, поэтомуявляется решением этого уравнения. Найдем второе частное решение по формуле. Сначала вычислим

.

Произвольную постоянную при вычислении неопределенного интеграла можно не писать, так как нас интересует лишь одно частное решение.

Теперь найдем

.

Заметим, что подынтегральное выражение в последнем интеграле является производной от функции , поэтому

.

(Постоянную здесь также можно не писать.)

Таким образом, второе частное решение исходного уравнения имеет вид

.

Проверим, что два полученных решения линейно независимы. Вычислим определитель Вронского:

при .

В рассматриваемой области , откуда следует, что решенияилинейно независимы. Тогда общее решение дифференциального уравнения будет иметь вид

,

где и- произвольные постоянные.◄

ТЕОРЕМА (о структуре общего решения ЛОДУ)

Пусть функции являются непрерывными наЛНЗ решениями ЛОДУn-го порядка . Тогда общее решение ДУ для любогоможно представить в виде

, где .

1. Линейные однородные уравнения с постоянными коэффициентами

Уравнение вида

,

где ,, называетсяЛОДУ n-ого порядка с постоянными коэффициентами.

Рассмотрим методы получения ФСР для ЛОДУ. Будем искать решение этого уравнения в виде подстановки Эйлера. Последовательно находим производные . Подставим их в дифференциальное уравнение

.

Так как , то. Из этого алгебраического уравнения и находится требуемое значение.

Алгебраическое уравнение n-го порядка называетсяхарактеристическим уравнением для ЛОДУ n-го порядка:

.

Такое характеристическое уравнение всегда имеет корнейс учетом кратности. Если все его корни различны, то ФСР состоит изфункцийи. Если среди корнейесть кратные и, например,корень кратности, то возникаетодинаковых функций, которые являются линейно зависимыми. Тогда строится другая система функций, которая уже будет линейно независимой.

Типовой пример

Найти общее решение уравнения: .

►Составим характеристическое уравнение, найдем его корни:

.

Составим систему и вычислим определитель Вронского

для любого , следовательно,

–ЛНЗ и образуют ФСР. Тогда – общее решение данного ЛОДУ.◄

Типовой пример

Найти общее решение уравнения .

►Найдем корни характеристического уравнения:

.

Следовательно, . Все корни различны. В итоге имеем

–ФСР данного ЛОДУ;

–общее решение.◄

Типовой пример

Дано ДУ ; найти его общее решение.

►Характеристическое уравнение:

имеет кратный корень .

Составим систему и вычислим определитель Вронского

, следовательно,

–ЛНЗ и образуют ФСР данного ЛОДУ.

–общее решение.◄

Типовой пример

Дано ДУ ; найти его общее решение.

►Характеристическое уравнение имеет два комплексно-сопряженных корня.Согласно предложенному алгоритму – ЛНЗ и образуют ФСР. Общее решение будет иметь вид .«Ограничиться» комплексной формой решения значило бы выйти за рамки нашего рассмотрения. Можно воспользоваться знаменитой формулой Эйлера

и получить из комплексной пары идве линейно независимыедействительные функции:

Запишем

–по формуле Эйлера.

Тогда общее решение будет иметь вид

.

Последнее представление считается более удобным.◄

Сформулируем общее правило, следуя которому составляется фундаментальная система решений.

Алгоритм построения ФСР для ЛОДУ n-го порядка с постоянными коэффициентами.

Фундаментальная система решений ЛОДУ с постоянными коэффициентами строится на основе характера корней характеристического уравнения.

1. Если действительный корень характеристического уравнения кратности, то ему соответствуетЛНЗ решений:

.

2. Если комплексно-сопряженная пара корней характеристического уравнения кратности, то ей соответствуетЛНЗ решений:

.

Совокупность всех ЛНЗ решений, соответствующих корням характеристического уравнения, образуют ФСР.

Типовой пример

Найти общее решение уравнения: .

►Характеристическое уравнение

имеет корни

.

Корень действительный и простой. Для комплексно-сопряженных корнейнаходим значения. Согласно алгоритму, составляем ФСР:. Общее решение однородного уравнения имеет вид:

◄

Типовой пример

Найти общее решение уравнения: .

►Характеристическое уравнение

имеет следующие корни: .

Корни действительные и простые. Для комплексно-сопряженных корнейнаходим значения. Применяя алгоритм, получаем ФСР; составляем общее решение:.◄

В частности, характеристическое уравнение для линейного однородного дифференциального уравнения с постоянными коэффициентами второго порядка

является квадратным: . Поэтому общее решение уравнения может иметь один из трех видов:

а) если дискриминант характеристического уравнения аего различные действительные корни, то решение уравнения выглядит как

;

б) если D = 0, характеристическое уравнение имеет один корень λ₀, и общее решение уравнения имеет вид

;

в) при D < 0 характеристическое уравнение имеет комплексно сопряженные корни , а общее решение уравнения записывается в форме

Типовые примеры

Найти общее решение уравнения.

1) .

►Составим и решим характеристическое уравнение Значит, общее решение записывается в виде:. ◄

2)

►Характеристическое уравнение имеет один действительный корень λ = 0 кратности 3 и два комплексно сопряженных корня: - 2 ± 3i. Так как е^0∙х = 1, общее решение записывается в форме (17) и (18):

.◄