
- •§1. Дифференциальные уравнения и их решение
- •7. Линейные уравнения первого порядка
- •2) Найти общее решение .
- •8. Уравнение Бернулли
- •9. Уравнения в полных дифференциалах
- •10. Уравнения вида и
- •11. Уравнения Лагранжа и Клеро
- •12. Определение типа дифференциального уравнения первого порядка
- •§2. Уравнения высших порядков
- •§3. Линейные дифференциальные уравнения и системы
- •Свойства линейного дифференциального оператора
- •Система из линейно независимых (лнз) на промежуткерешенийдля лодУn-го порядка называется фундаментальной системой решений (фср) этого уравнения.
- •Типовой пример Решить задачу Коши.
- •Решение неоднородного линейного уравнения с постоянными коэффициентами методом вариации постоянных
- •Вопросы промежуточного контроля
- •Типовые задания для контроля знаний и закрепления практических навыков
- •Вариант №2
7. Линейные уравнения первого порядка
Линейным уравнением первого порядка называют дифференциальное уравнение первого порядка, которое линейно относительно функции и ее производной, то есть уравнение вида
![]() .
.
Здесь
![]() ,
,![]() ,
,![]() – непрерывные функции от
– непрерывные функции от![]() .
В области, где
.
В области, где![]() ,
это уравнение равносильно уравнению
вида
,
это уравнение равносильно уравнению
вида![]() .
.
Линейное
уравнение в общем случае, то есть когда
![]() ,
называютнеоднородным
линейным уравнением первого порядка.
Если b
(x)
≡ 0, уравнение является однородным,
причем однородное линейное уравнение
– это уравнение с разделяющимися
переменными. На этом основан способ
решения неоднородных линейных уравнений
– метод
вариации постоянной.
Получив решение однородного уравнения
,
называютнеоднородным
линейным уравнением первого порядка.
Если b
(x)
≡ 0, уравнение является однородным,
причем однородное линейное уравнение
– это уравнение с разделяющимися
переменными. На этом основан способ
решения неоднородных линейных уравнений
– метод
вариации постоянной.
Получив решение однородного уравнения
![]() в видеy
= f
(x,
C),
считают, что решение исходного уравнения
имеет такой же вид, но С
= С (х)
– не постоянная, а функция от х,
вид которой можно определить, подставив
y
= f
(x,
C
(х))
в данное уравнение. Линейное неоднородное
уравнение решается и с помощью замены
в видеy
= f
(x,
C),
считают, что решение исходного уравнения
имеет такой же вид, но С
= С (х)
– не постоянная, а функция от х,
вид которой можно определить, подставив
y
= f
(x,
C
(х))
в данное уравнение. Линейное неоднородное
уравнение решается и с помощью замены
![]() .
.
Типовые примеры
1)
Найти общее решение уравнения
![]()
►Решим однородное уравнение
![]() .
.
Теперь будем искать решение неоднородного уравнения в виде
у
= С (х)∙е-2х.
![]() .
.
Подставим
y
и
y’
в исходное уравнение
![]() ,
,
где
![]() –
произвольная постоянная. Следовательно,
общее решение неоднородного уравнения
–
произвольная постоянная. Следовательно,
общее решение неоднородного уравнения
![]() ◄
◄
2) Найти общее решение .
►Это
линейное неоднородное уравнение.
Рассмотрим однородное:
![]() .
Решим его:
.
Решим его:![]() ,
,![]() ,
,![]() .
.
По
методу Лагранжа общее решение линейного
неоднородного уравнения ищем в виде
![]() ,
где
,
где![]() – неизвестная функция.
– неизвестная функция.
Подставим это выражение в исходное уравнение:
![]() .
.
Получим простейшее дифференциальное уравнение 1-го порядка:
![]() ,
,
![]() ,
,![]() .
.
Окончательно общее решение нашего уравнения имеет вид
![]() .
◄
.
◄
8. Уравнение Бернулли
К
линейному можно привести и уравнение
вида
![]() называемоеуравнением
Бернулли.
Для этого вводится новая функция
называемоеуравнением
Бернулли.
Для этого вводится новая функция
![]() ,
для которой
,
для которой![]() .
Разделим обе части уравнения (9) нау
п:
.
Разделим обе части уравнения (9) нау
п:
![]() или
или
![]() линейное уравнение для функцииz.
линейное уравнение для функцииz.
Типовой пример
Найти
общий интеграл уравнения
![]() .
.
►Разделим
обе части равенства на у2:
![]() и сделаем замену:
и сделаем замену:![]() .
Решим уравнение дляz:
.
Решим уравнение дляz:
![]() .
Однородное уравнение:
.
Однородное уравнение:
![]()
![]() .
Подставим полученные выражения в
неоднородное уравнение:
.
Подставим полученные выражения в
неоднородное уравнение:
![]()
![]() ◄
◄
9. Уравнения в полных дифференциалах
Дифференциальное
уравнение
![]() называетсяуравнением
в полных дифференциалах,
если существует такая функция двух
переменных
называетсяуравнением
в полных дифференциалах,
если существует такая функция двух
переменных
![]() ,
что
,
что![]() . Данное
равенство означает, что
. Данное
равенство означает, что![]() и
и![]() .
.
Известно,
что если в односвязной области
![]() частные производные
частные производные![]() и
и![]() непрерывны, то
непрерывны, то![]() является полным дифференциалом только
в том случае, когда выполняется равенство
является полным дифференциалом только
в том случае, когда выполняется равенство![]() .
.
В
этом случае функция
![]() ,
полным дифференциалом которой является
,
полным дифференциалом которой является![]() ,
выражается следующим образом:
,
выражается следующим образом:
![]() .
.
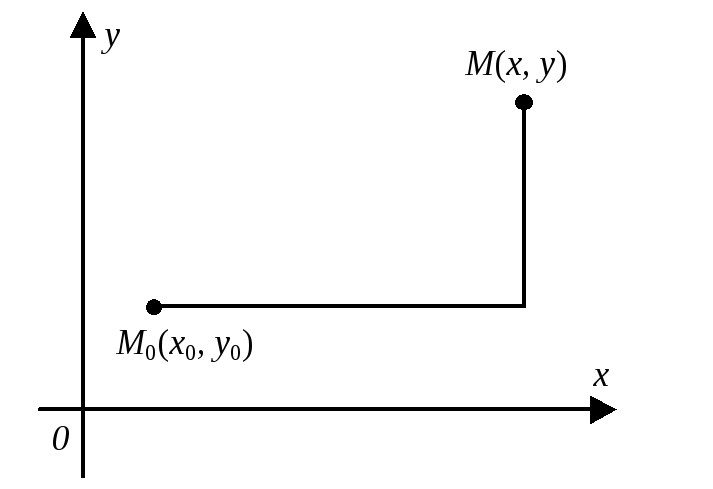
Рис. 1
Здесь
![]() – любая кривая в области
– любая кривая в области![]() ,
соединяющая фиксированную точку
,
соединяющая фиксированную точку![]() этой области, в которой
этой области, в которой![]() ,
с точкой
,
с точкой![]() .
В частности, если
.
В частности, если![]() имеет вид ломаной, изображенной на рис.
1, то формула принимает вид
имеет вид ломаной, изображенной на рис.
1, то формула принимает вид
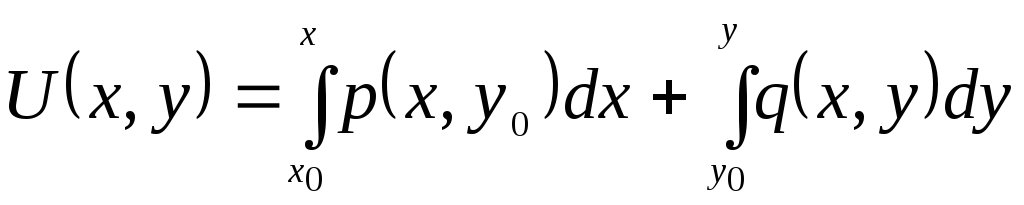 .
.
Так
как
![]() ,
то
,
то![]() (
(![]() – константа) и решение уравнения имеет
вид
– константа) и решение уравнения имеет
вид
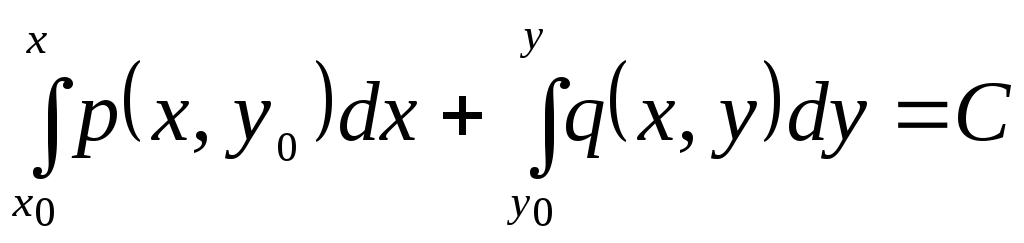 .
.
Другая эквивалентная формула решения уравнения имеет вид
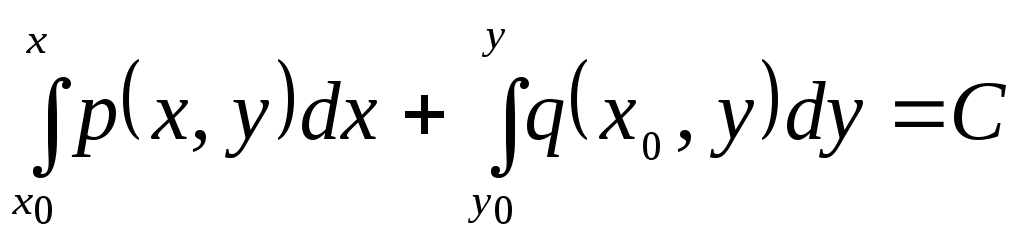 .
.
Здесь
в качестве
![]() и
и![]() берутся любые численные значения
берутся любые численные значения![]() и
и![]() ,
при которых
,
при которых![]() и
и![]() имеют смысл. Обычно
имеют смысл. Обычно![]() и
и![]() выбирают так, чтобы правая часть решения
имела более простой вид.
выбирают так, чтобы правая часть решения
имела более простой вид.
■▬▬▬►
2.
Если в области D
не выполнено условие
![]() ,
то иногда удается найти в D
такую функцию
,
то иногда удается найти в D
такую функцию
![]() ,
что уравнение
,
что уравнение
![]()
является в области D уравнением в полных дифференциалах.
Если
известно, что
![]() ,
где
,
где![]() –
известная дифференцируемая вD
функция, то интегрирующий
множитель
m
удовлетворяет дифференциальному
уравнению
–
известная дифференцируемая вD
функция, то интегрирующий
множитель
m
удовлетворяет дифференциальному
уравнению
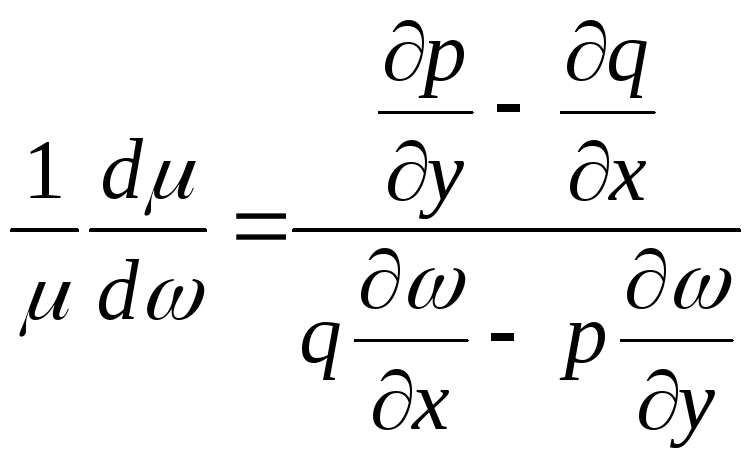 .
.
Если
известно, что
![]() ,
то
,
то![]() удовлетворяет уравнению
удовлетворяет уравнению
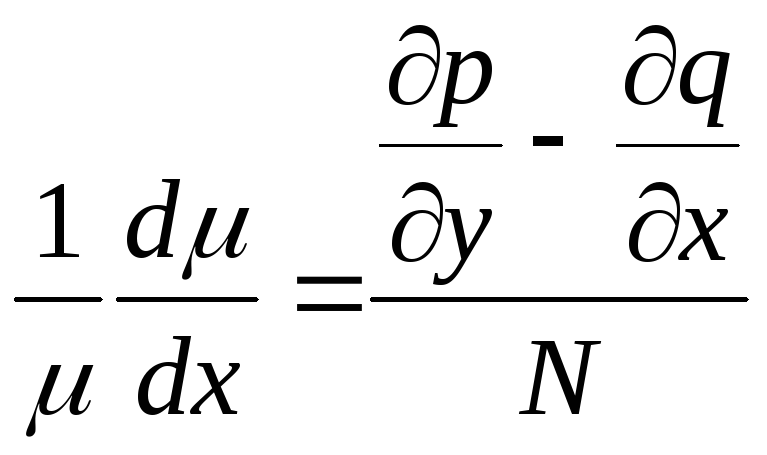 .
.
Если
известно, что
![]() ,
то
,
то![]() удовлетворяет уравнению
удовлетворяет уравнению
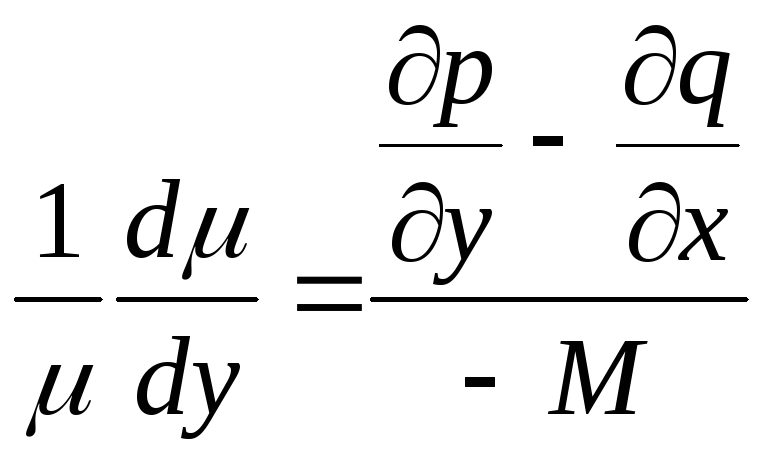 .
.
◄▬▬■
Типовой пример
Решить уравнение
![]() .
.
►Здесь
![]() ,
,![]() .
Выясним, является ли это уравнение
уравнением в полных дифференциалах.
Найдем
.
Выясним, является ли это уравнение
уравнением в полных дифференциалах.
Найдем![]() и
и![]() :
:
![]() ,
,
причем частные производные непрерывны. Применим формулу
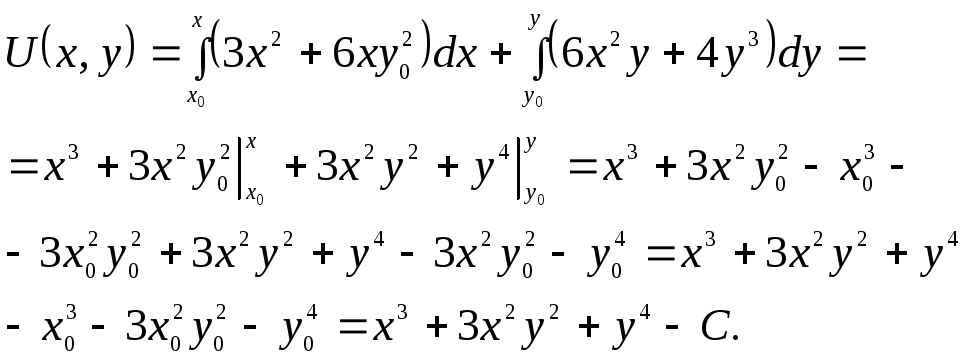
В
силу произвольности константы
![]() и произвольного выбора
и произвольного выбора![]() и
и![]() (которые также являются постоянными)
обозначим за единую константу
(которые также являются постоянными)
обозначим за единую константу![]() .
Тогда общий интеграл имеет вид
.
Тогда общий интеграл имеет вид
![]() .
.
Итак,
![]() – общее решение дифференциального
уравнения. ◄
– общее решение дифференциального
уравнения. ◄
Типовые примеры
1)
Решить задачу Коши для уравнения
![]() ,
еслиу(1)
= 1.
,
еслиу(1)
= 1.
►Проверим,
действительно ли перед нами уравнение
в полных дифференциалах:
![]() условие выполнено. Для поискаU
(x,
y)
зададим х0
= у0
= 0,
условие выполнено. Для поискаU
(x,
y)
зададим х0
= у0
= 0,
тогда
![]()
При х = у =1 найдем С из равенства ех + ху – еу = С: е + 1 – е = С, С = 1. Следовательно, искомое частное решение имеет вид
ех + ху – еу = 1. ◄
2)
Найти общее решение
![]() .
.
►Введем обозначения:
![]() .
.
Так
как![]() ;
;![]() ,
а следовательно
,
а следовательно![]() ,
то уравнение является уравнением в
полных дифференциалах. Его левая часть
есть полный дифференциал
,
то уравнение является уравнением в
полных дифференциалах. Его левая часть
есть полный дифференциал![]() ,
причем
,
причем
![]()
![]()
Далее
![]() ,
,
то есть
![]() ,
,
![]() ,
а,
,
а,![]() .
.
Общий интеграл исходного уравнения имеет вид U (x, y)=C или
![]() .
◄
.
◄
3)
![]() ,D
Ì
R2xy.
,D
Ì
R2xy.
►![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Ищем интегрирующий множитель. Выражение
![]() не
зависит от у.
не
зависит от у.
Считая
его доопределенным при
![]() ,
решаем уравнение
,
решаем уравнение![]() .
.
Имеем
![]() .
Прямая
.
Прямая![]() .
Очевидно, есть одно из решений исходного
уравнения. Считая
.
Очевидно, есть одно из решений исходного
уравнения. Считая![]() ,
умножаем обе части уравнения на
,
умножаем обе части уравнения на![]() ,
получаем уравнение
,
получаем уравнение![]() ,
откуда находим
,
откуда находим
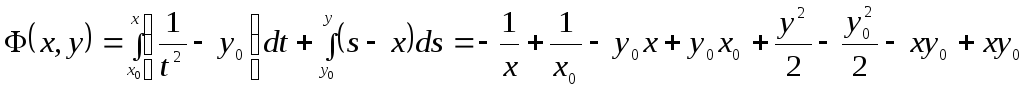
Следовательно,
![]() –общий
интеграл (решение
–общий
интеграл (решение![]() получается в общем интервале при С=¥).
◄
получается в общем интервале при С=¥).
◄
