ГЛАВА ?. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

§1. Дифференциальные уравнения и их решение

1. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, функцию и производные (или дифференциалы) этой функции.

Мы будем рассматривать уравнения, где неизвестная функция является функцией одной переменной. Такие уравнения называются обыкновенными дифференциальными уравнениями.

Уравнение вида называетсяобыкновенным дифференциальным уравнением п-го порядка. При этом порядком уравнения называется максимальный порядок входящей в него производной.

Функция, которая при подстановке в уравнение обращает его в тождество, называется решением дифференциального уравнения.

2. Дифференциальные уравнения 1-го порядка

Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида , связывающее между собой независимую переменную, искомую функцию и ее производную.

Частным решением такого уравнения является любая функция y = f (x), которая при подстановке в уравнение обращает его в тождество для всех допустимых значений переменной.

Множество всех решений уравнения называется его общим решением, или общим интегралом. Оно имеет вид y=f(x,С) – такой, что любое частное решение получается при некотором значении произвольной постоянной С, и наоборот, любое фиксированное значение С дает функцию, являющуюся решением уравнения.

Задача Коши (задача с начальным условием). Пусть функция определена в областиD, точка . Требуется найти решение уравнения

,

удовлетворяющее начальному условию

(начальное условие часто записывают в форме ).

Теорема Коши (существования и решения задачи Коши). Если в области D функция непрерывна и имеет непрерывную частную производную, то для любой точкив окрестности точкиx₀ существует единственное решение задачи Коши.

Для существования решения в окрестности точки x₀ достаточно только непрерывности функции ; условие непрерывностиобеспечивает единственность этого решения.

3. Уравнения с разделяющимися переменными

Дифференциальное уравнение первого порядка вида

называется уравнением с разделяющимися переменными. Его можно привести к равенству

,

откуда .

Если существуют первообразные ифункцийf (x) и , общее решение данного уравнения имеет вид

4. К уравнению с разделяющимися переменными можно привести и уравнение вида , гдеa, b, c – постоянные. Для этого вводится новая функция z = ax + by + c. Поскольку

то для z получаем уравнение с разделяющимися переменными:

Типовой пример

Найти общее решение уравнения .

►Разделим переменные:

Обратите внимание на форму записи произвольной постоянной: если вид общего интеграла можно упростить потенцированием, удобно представить произвольную постоянную как логарифм другой произвольной постоянной. Тогда общий интеграл можно записать так: ◄

Типовой пример

Найти общее решение: .

►Преобразуем данное уравнение:

.

Это уравнение с разделяющимися переменными. Разделим переменные

Интегрируем обе части неравенства:

Последнее равенство является общим интегралом исходного уравнения. ◄

Типовой пример

Найти частное решение уравнения , удовлетворяющее условиюу(4) = 1.

►Пусть Решим уравнение дляz:

При х = 4, у = 1 получаем:

6 – 4 ln 5 = 4 + C, откуда С = 2 – 4 ln 5.

Следовательно, частное решение имеет вид: ◄

Задача об эффективности рекламы. Пусть торговой фирмой реализуется некоторая продукция, о которой в момент времени из рекламы получили информациючеловек из общего числапотенциальных покупателей. Далее эта информация распространяется посредством общения людей, и в момент временичисло знающих о продукции людей равно. Сделаем предположение, что скорость роста числа знающих о продукции пропорциональна как числу осведомленных в данный момент покупателей, так и числу неосведомленных покупателей. Это приводит к дифференциальному уравнению

.

Здесь – положительный коэффициент пропорциональности. Из уравнения получаем равенство дифференциалов двух функций аргумента:

.

Интегрируя левую и правую части, находим общее решение дифферен­циального уравнения:

.

В общее решение входит неопределенная константа . Полагая, получим равенство

,

из которого определим функцию :

.

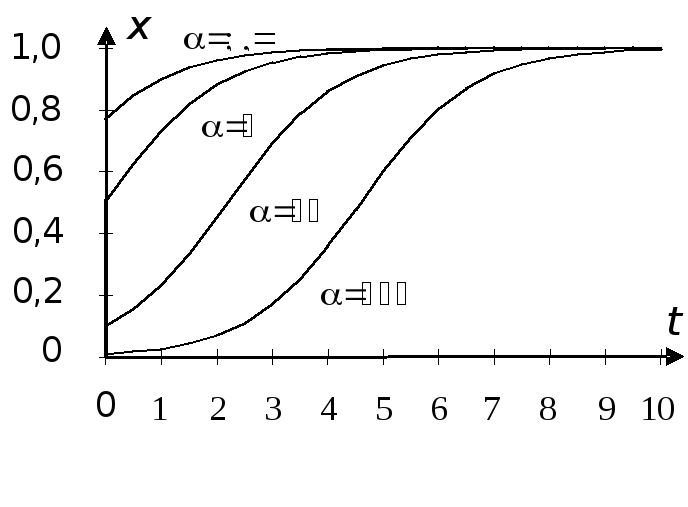
Здесь . Такого вида функция называется логистической, а её график – логистической кривой. Если теперь учесть, что х(0) = х₀, и положить х₀ = N/, где  > 0, то можно найти значение константы Е. Логистичеcкая функция примет вид

.

На рисунке приведены примеры логистических кривых, полученных при различных значе­ниях . Здесь величина N условно принималась за 1, а величина k бралась равной 0,5. С помощью логисти­ческой функции описыва­ются многие экономические, социаль­ные, технологичес­кие и биологические про­цессы, например, постоян­ный рост продаж, распростра­нение слухов, распространение техни­ческих новшеств, рост популяции определенного вида животных и прочее.

Пример

Рассмотрим процесс возрастания денежной суммы, положенной в банк, при условии начисления сложных процентов в год. Пустьобозначает начальную денежную сумму, а– денежную сумму по истечениилет. Если бы проценты начислялись один раз в год, мы бы имели

,

где =0, 1, 2, 3,.. Если бы проценты начислялись два раза в год (по истечении каждого полугодия), то мы имели бы

,

где =0, 1/2, 1, 3/2,.. Вообще, если проценты начисляютсяраз в год ипринимает последовательно значения, то

_,

то есть . Если обозначить, то предыдущее равенство перепишется так:.

Неограниченно увеличивая (при,), мы в пределе приходим к процессу возрастания денежной суммы при непрерывном начислении процентов:, то есть при непрерывном изменениизакон возрастания выражен дифференциальным уравнением 1-го порядка с разделяющимися переменными. Отметим, что здесь– неизвестная функция,– независимая переменная,– постоянная. Решение данного уравнения имеет вид, или, где черезобозначено.

Учитывая начальное условие , найдем:, следовательно,. Решение имеет вид

.

5. Однородные уравнения

Рассмотрим еще один класс уравнений, которые путем подстановки сводятся к уравнениям с разделяющимися переменными.

Функция называетсяоднородной измерения (степени) m (mÎR), если _. Так, x³ – 3xy² + +4y³ – однородная функция степени 3; ln x – ln y – однородная функция нулевой степени.

Дифференциальные уравнения , правая часть которых является однородной функцией нулевой степени, называютсяоднородными уравнениями. Если в некоторой области D Ì R²xy функции инепрерывные и однородные с одним измерением, то дифференциальное уравнение первого порядкаявляетсяоднородным дифференциальным уравнением в области D.

Однородное уравнение, которое можно записать в форме

,

может быть сведено к уравнению с разделяющимися переменными для функции . При этоми уравнение дляt примет вид: уравнение с разделяющимися переменными.

6. К однородному уравнению, в свою очередь, можно привести уравнение вида

при условии . При этом производится параллельный перенос в плоскости (х, у) – такой, чтобы начало координат совместилось с точкой (x₀; y₀) пересечения прямых ax + by + c = 0 и a₁x + b₁y + c₁ = 0. Тогда в

новых координатах уравнение будет выглядеть как

, или – однородное уравнение.

Типовой пример

Найти общий интеграл уравнения .

►Разделим обе части равенства на х:

и сделаем замену . Тогдаобщий интеграл уравнения. ◄

Типовой пример

Найти общее решение:.

►Так как функциии— однородные второго измерения

то данное уравнение – однородное. Сделаем замену: где– новая неизвестная функция.. Тогда,. Далее имеем,.

Это уравнение с разделяющимися переменными. Решаем его:

, ,.

В последнее выражение вместо подставим значение.

Получим общий интеграл: . Выразив отсюда, найдем общее решение исходного уравнения:. ◄

Типовой пример

Найти общее решение уравнения .

►Решим систему уравнений 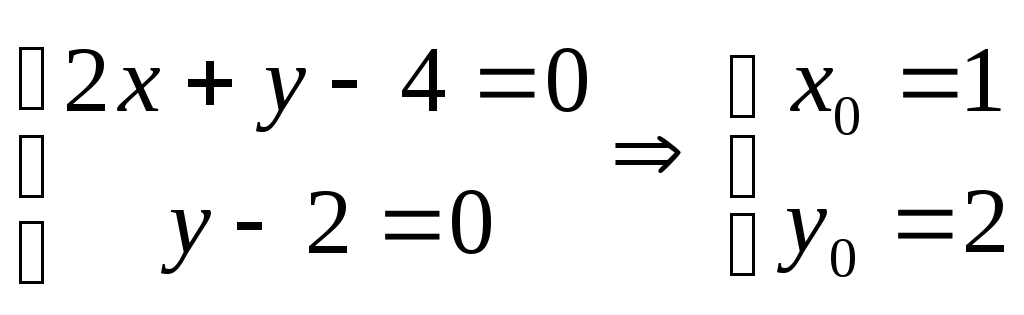. Тогда, и в новых переменных (с учетом того, что) получаем уравнение.

Замена приводит к уравнению

После упрощения и обратной замены получаем общее решение в виде:

. ◄