
14-es / ЭС - Информатика (ИСФ) / умк_Спиридонов_Информатика_ч.1_2013
.pdf
Корень уравнения геометрически представляет собой абсциссу точки пере- сечения, касания (рис. 6.1) или другой общей точки (рис. 6.2) графика функции у = f(х) и оси OX.
Рис. 6.1. Графики функции y = f(x)
Отделить корень уравнения – значит найти такой конечный промежу- ток, внутри которого имеется единст- венный корень данного уравнения. От- деление корней уравнения можно выполнить аналитически, исследовав данную функцию или графически, по- строив график функции у = f(х), по ко- торому можно судить о том, в каких промежутках находятся точки пересе- чения его с осью ОX.
Рис. 6.2. Пример отделения корня методом разбиения функции на 2
6.2.2. Уточнение корня методом половинного деления
Допустим, что искомый корень уравнения отделен, т.е. найден отре- зок [а, b], на котором имеется один и только один корень уравнения. Лю- бую точку этого отрезка можно принять за приближенное значение корня. Погрешность такого приближения не превосходит длины [а, b]. Следова- тельно, задача отыскания приближенного значения корня с заданной точ- ностью ε сводится к нахождению отрезка [а, b], содержащего только один корень уравнения. Эту задачу обычно называют задачей уточнения корня.
Задача уточнения корня сводится к делению отрезка пополам, с каж- дым шагом выделяя новый кусок отрезка [a, c] или [c, b] до тех пор, пока значение не будет x ≈ 0. Примерная схема алгоритма решения уравнения f(x) = 0 методом половинного деления представлена на рисунке 6.3.
141

Рис. 6.3. Блок-схема алгоритма решения нелинейного уравнения методом половинного деления
6.2.3. Метод хорд (секущих)
Метод хорд, или метод секущих, приближенного решения уравнения y = f(x) имеет следующую геометрическую иллюстрацию: вместо точки пересечения оси ОХ и графика функции f(x), входящей в это уравнение, рассматривается точка пересечения данной оси и отрезка прямой, соеди- няющей концы дуги графика (рис. 6.4). Если известно (n – 1)- е приближе- ние, то n-е вычисляется по формуле
xn = |
bf (xn−1) − xn−1 f (b) |
|
при f(b)f ²(x) > 0 |
|||
|
f (xn−1) - f (b) |
|||||
|
|
|
|
|||
где n = 1, 2, 3, …, |
|
af (xn−1) − xn−1 f (a) |
|
|||
или xn |
= |
при f(a)f ²(x) > 0. |
||||
f (xn−1) - f (a) |
|
|||||
|
|
|
|
|||
Оценка абсолютной погрешности определяется формулой
ξ − xn |
|
≤ |
|
f (xn ) |
, μ = max |
|
′ |
|
|
′ |
|
|
|
|
|||||||
|
|
|
|
f (x) |
|
, |
f (x) ¹ 0 . |
|||
|
|
μ |
||||||||
|
|
|
|
142 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Рис. 6.4. Графики, иллюстрирующие метод хорд
6.2.4. Метод касательных
Метод касательных (или метод Ньютона) отличается от метода хорд тем, что здесь рассматривается не секущая, соединяющая концы дуги гра- фика, а касательная к графику. Точка пересечения касательной с осью OX дает приближенное значение корня (рис. 6.5).
В методе касательных (n + 1)-е приближение вычисляется по формуле
xn +1 = xn - |
|
f ( xn ) |
||
|
|
|
, (n = 1, 2, 3, …), |
|
|
/ |
|
||
|
f |
( xn ) |
||
в которой за нулевое приближение x0 принимается такое значение из отрез- ка [а, b], для которого выполняется условие при f(x0)f ²(x) > 0.
Оценка погрешности, как и в ме- тоде хорд, определяется формулой
Рис. 6.5. График, иллюстрирующий метод касательных
x - xn |
|
£ |
|
f (xn ) |
, где m = max |
|
′ |
|
|
|
′ |
|
|
|
|
|
|||||||
|
|
|
f |
(x) |
|
, |
f |
(x) ¹ 0 . |
|||
|
|
m |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
143

6.2.5. Метод итераций
Если каким-либо способом получено приближенное значение х0 кор- ня уравнения f(x) = 0, то уточнение корня можно осуществить методом по- следовательных приближений или методом итераций (рис. 6.6). Для этого уравнение f(x) = 0 представляют в виде
х = ϕ(х),
что всегда можно сделать и притом многими способами, например
х = х + сf(х),
где с – произвольная постоянная,
xn = ϕ(xn-1).
Процесс последовательного вычисления чисел xn (n = 1, 2, 3, ...) по этой формуле называется методом последовательных приближений или методом итераций. Процесс итераций сходится, если выполнено условие ϕ′(x) ≤ q < 1на отрезке [а, b], содержащем корень.
а)
б)
Рис. 6.6. Графики, иллюстрирующие условия итерационных процессов: а – сходимости; б – расходимости
144

6.3. Методы решения систем линейных уравнений
Инженеру часто приходится решать алгебраические и трансцендент- ные уравнения, что может представлять собой самостоятельную задачу или являться частью более сложных задач. В обоих случаях практическая ценность метода в значительной мере определяется быстротой и эффек- тивностью полученного решения. Выбор подходящего метода для решения уравнений зависит от характера рассматриваемой задачи. Задачи, сводя- щиеся к решению алгебраических и трансцендентных уравнений, можно классифицировать по числу уравнений (рис. 6.7) и в зависимости от пред- лагаемого характера и числа решений.
Рис. 6.7. Классификация уравнений
Одно уравнение будем называть линейным, алгебраическим или трансцендентным в зависимости от того, имеет ли оно одно решение, n решений или неопределенное число решений. Систему уравнений будем называть линейной или нелинейной в зависимости от математической при- роды входящих в нее уравнений.
Способы решения систем линейных уравнений делятся на две группы:
1)точные методы, представляющие собой конечные алгоритмы для вычисления корней системы (решение систем с помощью обратной матрицы, правило Крамера, метод Гаусса и др.),
2)итерационные методы, позволяющие получить решение систе- мы с заданной точностью путем сходящихся итерационных процессов (ме- тод итерации, метод Зейделя и др.).
145
Вследствие неизбежных округлений результаты даже точных мето- дов являются приближенными. При использовании итерационных мето- дов, сверх того, добавляется погрешность метода. Эффективное примене- ние итерационных методов существенно зависит от удачного выбора начального приближения и быстроты сходимости процесса.
Пусть дана система линейных алгебраических уравнений (СЛАУ) с n неизвестными:
|
|
|
a11x1 + a12 x2 + ... + a1n xn = a1n +1 |
||||||||||||
|
|
|
|
|
+ a |
|
|
|
|
+ ... + a |
|
|
|
= a |
|
|
|
|
a |
x |
22 |
x |
2 |
2n |
x |
n |
2n +1 |
||||
|
|
|
|
21 1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.1) |
|
|
|
..................................................... |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an1x1 + an2 x2 + ... + ann xn = ann +1 |
||||||||||||
или в матричной форме АХ = В, |
|
|
|
|
|
|
|
||||||||
|
|
a11 |
_ a12 ...a1n |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
a21 |
_ a22 ...a2n |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
A = (aij) = ..................... |
|
– есть матрица коэффициентов; |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
an1 |
_ an2 ...ann |
|
|
|
|
|
|
||||||
|
|
a1n +1 |
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2n +1 |
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
B = |
|
|
X = |
|
|
|
– соответственно столбец свободных членов |
|||||||
|
... |
и |
... |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ann +1 |
|
|
xn |
|
|
|
|
|
|
|
|
|
|
и столбец неизвестных.
Если матрица А неособенная, т.е. det A ¹ 0, то система имеет единст- венное решение. Методы решения таких систем разбиваются на две груп- пы: точные и приближенные.
6.3.1. Метод Гаусса
Пусть в системе (6.1) коэффициент а11 ¹ 0. Назовем а11 ведущим элементом первой строки. Умножив первое уравнение системы (6.1) на
– а21/а11 и прибавив ко второму, получим новое уравнение, в котором коэффициент при x1 обращается в нуль. Умножив первое уравнение сис-
146
темы на – а31/а11 и прибавив к третьему, получим новое уравнение, в кото- ром коэффициент при x1 обращается в нуль. Аналогично преобразуем ос- тальные уравнения.
Полагая, что в полученной системе коэффициент а¢22 ¹ 0. Умножив второе уравнение новой системы на – а¢32/а¢22 и прибавив к третьему, полу- чим новое уравнение, в котором коэффициент при x2 обращается в нуль. Аналогично преобразовываем остальные уравнения. В конечном итоге по- лучим систему, эквивалентную треугольной матрице:
x1 + a12¢ x2 + ... + a1¢n xn = a1¢n+1
x2 + ... + a2¢ n xn = a2¢ n+1
..........................
xn = a¢nn+1
6.3.2.Метод простой итерации
Пусть задана система линейных уравнений:
|
a11x1 + a12 x2 + ... + a1n xn = a1n+1, |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a21x1 + a22 x2 + + a2n xn... = a2n+1, |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
..................................................... |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a x + a x + + a x... = a . |
|
||||||||||||||||
|
n1 1 n2 2 |
|
|
nn n |
nn+1 |
|
|
|||||||||||
Для реализации метода итераций необходимо привести систему к виду |
||||||||||||||||||
|
x = - |
1 |
(a x + + a x - a |
|
|
|||||||||||||
|
), |
|||||||||||||||||
|
|
|||||||||||||||||
1 |
12 2 |
|
|
|
1n n |
1n+1 |
|
|
||||||||||
|
|
a11 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x2 = - |
|
|
|
|
(a21x1 |
+ + a2n xn... - a2n+1), |
||||||||||||
|
|
|
||||||||||||||||
|
|
|
a22 |
|
|
|
|
|
|
|
|
|
||||||
..................................................... |
|
|
||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
x = - |
|
(a x + a x + - a... |
|
). |
||||||||||||||
|
|
|
||||||||||||||||
|
n |
|
|
|
|
n1 1 |
|
n2 2 |
nn+1 |
|
||||||||
|
|
|
ann |
|
|
|
|
|
|
|
|
|
||||||
Коэффициенты полученной системы должны удовлетворять сле- |
||||||||||||||||||
дующему условию сходимости: |
|
aii |
|
> ∑ |
|
aij |
|
, |
i = 1… |
n, т.е. модули диаго- |
||||||||
|
|
|
|
|||||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i¹ j |
|
|
|
|
|
|
|
|
нальных коэффициентов для каждого уравнения должны быть больше мо- дулей остальных коэффициентов, не считая свободных членов.
147

6.4. Приближенное вычисление определенных интегралов
6.4.1. Формулы прямоугольников
Формула левых прямоугольников (рис. 6.8, а)
b |
n−1 |
= h( y0 + y1 + y2 + ... + yn−1) ; |
∫ f (x)dx ≈ h ∑ yk |
||
a |
k =0 |
|
формула правых прямоугольников (рис. 6.8, б)
b |
n |
= h( y1 + y2 + ... + yn ) , |
∫ f (x)dx ≈ h ∑ yk |
||
a |
k =1 |
|
где h = (b – a) /n, yk = f(xk), |
xk = a + kh, (k = 0, 1, 2, …, n). |
|
Абсолютная погрешность метода прямоугольников определяется не- равенством
|
|
|
≤ |
(b − a)2 M |
, где M = max |
|
′ |
|
|
|
|
|
|
|
|
||||||
|
Rn |
( f ) |
|
|
f (x) |
|
. |
|||
2n |
||||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.8. Метод прямоугольников
6.4.2. Формула трапеций
b
∫ f (x)dx ≈ h( y0 / 2 + y1 + y2 + ... + yn / 2) ,
a
где h = (b – a )/n, yk = f(xk), xk = a + kh, (k = 0, 1, 2, …, n).
Правая часть этой формулы выражает площадь фигуры, состоящей из трапеций, высота каждой из которых равна h (рис. 6.9). Остаточный член приближенной формулы трапеций
|
≤ |
(b − a)3 M |
|
где M = max |
|
′′ |
|
. |
|
|
|
|
|||||||
Rn |
, |
||||||||
|
f (x) |
|
|||||||
|
|
12n |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
148
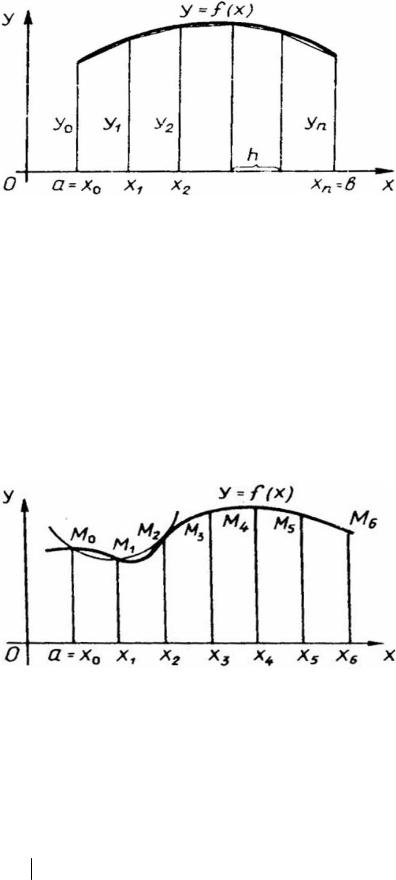
Рис. 6.9. Метод трапеций
6.4.3. Формула парабол
Формула парабол (или формула Симпсона) имеет вид
b |
|
h |
|
|
|
∫ f (x)dx ≈ |
( y0 + 4( y1 + y3 + ... + y2n−1) + 2( y2 + y4 + ... + y2n−2 ) + y2n ) , |
||||
|
|||||
a |
3 |
|
|
||
|
|
|
|
||
где h = (b-a) / (2n), yk = f(xk), xk = a + kh, (k = 0, 1, 2, …, 2 |
n). |
||||
|
Правая часть формулы парабол выражает площадь фигуры, состав- |
||||
ленной из параболических трапеций x0M0M2x2, x2M2M4x4 |
(рис. 6.10). |
||||
Рис. 6.10. Метод парабол
Дуга M0M1M2 графика подынтегральной функции здесь заменена ду- гой параболы, проходящей через точки M0 M1 M2. Аналогичная замена произведена и остальных дуг. Для остаточного члена формулы парабол выполняется неравенство
R |
|
≤ |
(b − a)5 M |
, |
где M = max |
|
f (IV ) (x) |
|
. |
|
|
|
|||||||
|
|
|
|||||||
|
|
|
|
||||||
n |
|
|
180(2n)4 |
|
|
|
|
|
|
|
|
|
|
149 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.5. Приближенное решение дифференциальных уравнений
6.5.1. Интегрирование дифференциальных уравнений с помощью рядов
Решения многих дифференциальных уравнений не выражаются в эле- ментарных функциях. В этих случаях пользуются приближенными методами интегрирования дифференциальных уравнений. Одним из таких методов яв- ляется представление решения уравнения в виде степенного ряда; сумма ко- нечного числа членов этого ряда будет приближенно равна искомому реше- нию. Указанный степенной ряд находят способом неопределенных коэф- фициентов или способом, основанным на применении ряда Тейлора.
Способ неопределенных коэффициентов особенно удобен в применении к линейным уравнениям и состоит в следующем. Если все коэффициенты уравнения и свободный член разлагаются в ряды по степе- ням, сходящиеся в интервале (а – h, а + h), то искомое решение у = у{х) также представляется степенным рядом сходящимся в том же интервале
y(x) = C0 + C1(x − a) + C2 (x − a)2 + ... + Cn (x − a)n .
Подставляя в уравнение функцию у(х) и ее производные, приравни- вают коэффициенты при одинаковых степенях. Из полученных при этом уравнений и заданных начальных условий находят коэффициенты. Способ, основанный на применении ряда Тейлора – Маклорена, заключается в по- следовательном дифференцировании данного уравнения
′ |
|
′′ |
|
2 |
|
|
y |
(n) |
(a) |
|
n |
|
|
|
y (a) |
|
|
|
|
|
|
||||||
y(x) = y(a) + y (a)(x − a) + |
|
(x − a) |
|
+ |
... + |
|
|
|
(x − a) |
|
. |
||
2! |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
n! |
|
|
|
|||
Это дает возможность |
найти |
значения |
производных, |
входящих |
|||||||||
в выражения для коэффициентов ряда, являющегося решением уравнения.
6.5.2. Метод Эйлера
Пусть требуется решить задачу Коши: найти решение дифференци- ального уравнения
у' = f(х,у),
удовлетворяющее начальному условию у(х0) = у0.
При численном решении этого уравнения задача ставится так: в точ- ках х0, x1, х2, ..., xn найти приближения уk (k = 0, 1, 2, ..., n) для значений точного решения y(хk). Разность хk = хk-1 – хk называется шагом сетки. Во многих случаях величину хk принимают постоянной h, тогда
хk = хk – 1 + kh (k = 0, 1, 2, ..., n).
150
