
Мальханов - Общая Физика
.pdf

ли расстояние от щелей до экрана выбирать много больше расстояния между щелями, тогда интерференционные полосы на экране становятся практически прямолинейными. Рассмотрим интерференцию от двух таких щелей.
x
|
|
A |
r2 |
r1 |
x |
S2 |
|
O2 |
d |
|
O |
S1 |
D |
O1 d/2 |
Найдем разность хода лучей в точке A
r12 = D2 + (x + d/2)2, r22 = D2 + (x - d/2)2.
Вычтем почленно эти равенства
r12 – r22 = 2xd, r1 + r2 2D ∆ = r1 – r2 = x d / D.
Угол α , под которым из точки A , а вообще из произвольной точки экрана видно расстояние между щелями называют углом схождения интерферирующих лучей.
α ≈ Sin α ≈ d / D ∆ = x α.
Используем соотношение, связывающее разность фаз и разность хода лучей, имеем
δ = 2π∆ / λ = 2πxα / λ.
Подставим разность фаз в формулу для результирующей интенсивности, имея в виду, что I1 = I2 = I′
I = 2I′ [ 1 + Cos (2παx/λ) ].
Таким образом данная формула применительно к конкретной экспериментальной схеме позволяет проследить зависимость интенсивности интерфе-
341


2 1
|
S1 |
ϕ |
d tg ψ |
n ψ
ψ |
S2/2 = d/Cos ψ d |
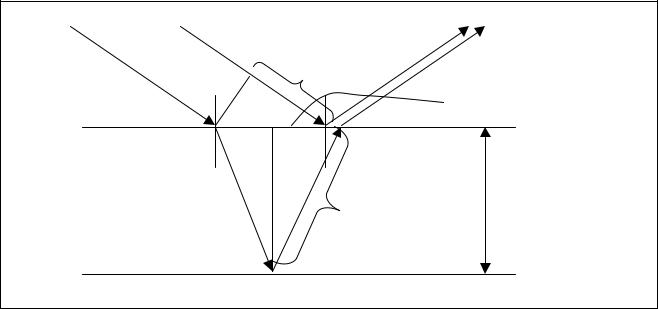
∆ = n S2 – S1
S1 = 2 d tg ψ Sin ϕ, S2 = 2 d n / Cos ψ. (Sin ϕ/Sin ψ = n Sin ϕ = n Sin ψ (исключим угол ϕ).
∆ = 2 d n (1 – Sin2 ψ) / Cos ψ = 2 d n Cos ψ.
С учетом эффекта Ллойда формула приобретает вид такой же как и в варианте
1 .
∆ = 2 d n Cos ψ + λ/2.
Разность хода можно выразить также через угол падения
n Cos ψ = n (1 – Sin2 ψ)1/2 = (n2 – n2 Sin2 ψ)1/2 = (n2 – Sin2ϕ)1/2. ∆ = 2 d ( n2 – Sin2 ϕ)1/2 + λ/2.
Зная разность хода лучей, можно рассчитывать координаты минимумов и максимумов в чем и состоит иногда задача интерференции.
§ 13 Дифракция
1-е определение. Отклонение от прямолинейного распространения электромагнитного излучения, если оно не может быть истолковано как результат
344

отражения, преломления или изгибания электромагнитного излучения в средах с непрерывно меняющимся показателем преломления.
Всякая дифракционная задача, если ее рассматривать более строго сводится к нахождению решений уравнений Максвелла при наличии начальных и граничных условий.
2-е определение. Совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонениями от законов геометрической оптики. К условиям наблюдения дифракционных явлений необходимо отнести, кроме наличия собственно волнового процесса и неоднородностей, одинаковый порядок величин размеров неоднородностей и длины волны. По характеру волнового фронта дифракцию разделяют на
1.Дифракцию Фраунгофера (Ф. Йозеф, немецкий физик, 1787-1826 гг.) – практически плоский волновой фронт (далеко от источника и относительно малая поверхность).
2.Дифракция Френеля (Огюстен Жан Ф., Франция, 1788-1827гг.) – волновой
фронт, имеющий ярко выраженную сферичность. Зоны Френеля.
Согласно принципу Гюйгенса-Френеля интенсивность волн в данной точке можно найти суммирую действие каждой точки волнового фронта, а в пределе интегрируя по всей волновой поверхности. Однако, такая процедура практически чрезвычайно сложна, поэтому понадобились иные методы. Один из них является метод зон Френеля
|
|
|
… … … |
|
|
|
|
r + 4λ/2 |
|
|
|
|
r + 3λ/2 |
|
|
|
|
r + 2λ/2 |
|
|
|
|
r + λ/2 |
|
|
|
S |
O |
P |
|
|
a |
b = r |
|
Определим (вслед за Френелем) амплитуду волнового процесса, возбуждаемого |
||||
в ( ) |
P |
сферической волной, распространяющейся в однородной изотропной |
||
|
|
|
345 |
|



1. |
2. |
3.
2.Откроем две первые зоны Френеля (m = 1 и 2 ). Получим внутри темное пятно, окруженное световым кольцом.
3.Откроем три первые зоны. Получим чередование светлых и темных колец, начиная от центрального светлого пятна.
И так далее … . Можно отметить закономерность:
m – нечетное – светлое пятно в центре, m – четное - в центре темное пятно.
Если закрыть все четные или нечетные зоны Френеля, то оставшиеся зоны усилят действие друг друга.
Рассчитаем связь между размерами отверстия и числом зон Френеля, укладывающихся в этом отверстии. Пусть D – диаметр отверстия, a и b соответственно расстояния от отверстия до источника и точки P на экране. С центрами в точках S и P проведем сферические поверхности волновых фронтов, укладывающихся в размер отверстия.
Рассмотрим треугольник OSA согласно рисунку. Здесь h = OF – расстояние от волновой поверхности до отверстия вдоль прямой SP .
348

|
A |
|
h << a, b |
|
|
|
h |
|
|
|
E |
F |
|
|
S |
O |
|
P |
|
a |
|
|
b |
|
(D/2)2 = a2 – (a – h)2 2 a h = 2 a OF, (D/2)2 2 b OE |
|
|||
OF = D2 / 8a, OE = D2 / 8b EF = OF + OE = D2 (1/a + 1/b) / 8. |
|
|||
Если разделить отрезок EF на |
λ/2 |
, то получим число зон Френеля, уклады- |
||
вающихся в нем. Если |
m получится целым, то D/2 = R m – есть радиус |
m – й |
||
зоны. |
|
|
|
|
m = EF / (λ/2) = D2 (1/a |
+ 1/b) / 8 (λ/2) = R m2 (1/a + 1/b) / λ |
|
||
R m2 = m λ / (1/a + 1/b). |
|
|
|
|
Пусть λ = 0.6 мкм, m = 1, a = b = 1 см R m = 5.5 10 – 5 м = 55 мкм. Для a = b |
||||
= 1 м Rm = 5.5 10 – 4 м = 0.55 мм. |
|
|
||
Плоская волна (дифракция в смысле Фраунгофера) может быть аппрок- |
||||
симирована удалением источника S |
на бесконечность (a → ∞). |
|
||
S |
|
|
P |
|
|
|
|
349 |
|
