CHAPTER 6

Subroutines and Modules

Good software should be configured as a set of interacting modules rather than one large program working straight through from beginning to end. There are many advantages to modular programming, which is almost mandatory when code lengths exceed a few hundred lines or when a project is being developed by a team.

What form should should such modules take? In order to answer this question we will look at the use of program structures designed to facilitate this modular approach and the instructions associated with it.

After completing this chapter you will:

•Appreciate the need for modular programming.

•Have an understanding of the structure of the stack and its use in the call–return subroutine and interrupt mechanisms.

•Understand the term nested subroutine.

•See how parameters can be passed to a subroutine, by copy or reference, and altered or returned to the caller.

•Be able to write a subroutine having a minimal impact on its environment.

•Be able to synthesize a software stack to open and close a frame in the Data store to pass parameters and provide a temporary workspace.

Take a look at the inside of your personal computer. It will probably look something like the photograph in Fig. 6.1, with a motherboard hosting the MPU, assorted memory and other support circuitry, and a variable number of expansion sockets. Into this will be plugged a disk controller card and a video card. There may be others, such as a soundboard, modem or network card. Each of these plug-in cards has a distinct and separate logical task and they interact via the services supplied by the main board – the motherboard.

There are many advantages to this modular construction.

•Flexibility; that is it is relatively easy to upgrade or reconfigure by adding or replacing plug-in cards.

•Can reuse from previous systems.

•Can buy in standard boards or design specialist boards in-house.

•Easy to maintain.

140 The Quintessential PIC Microcontroller

100 ms delay

Subroutine return

Program call More program call Even more program

Main flow

Fig. 6.2 Subroutine calling.

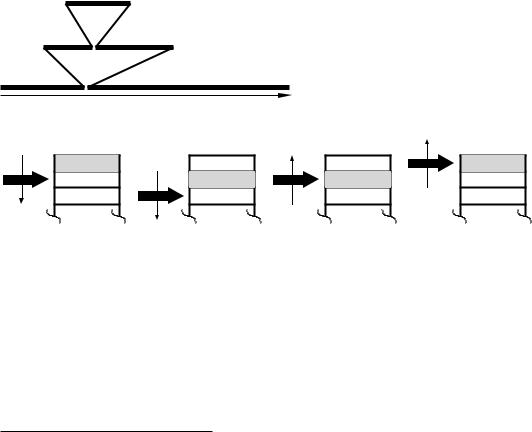
The problem really is how to get back again! Somehow the MPU has to remember from where in the caller program the subroutine was entered so that it can return to the next instruction in the caller’s sequence. This can be seen in Fig. 6.2, where the jumping-o point can be from anywhere in the main program, or indeed from another subroutine – the latter process is called nesting – see Fig. 6.4.

One possibility is to place this address in a designated Address register or memory location prior to jumping o . This can then be moved back into the PC at the end of the subroutine as the return mechanism. This approach breaks down whenever one subroutine wishes to call another. Then the secondary subroutine will overwrite the return address of the first, and the main program can never be regained. To get around this problem, more than one register or memory location could be used to hold a stack of return addresses. This last-in first-out stack structure is shown in Fig. 6.3(a).

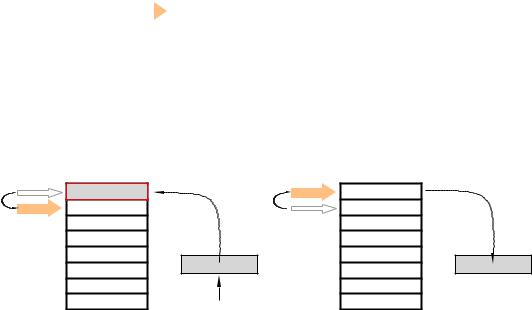
The 14-bit core PICs have a stack of eight 13-bit registers which are exclusively used to hold subroutine return addresses.3 This structure, shown in Fig. 6.3, is known as a hardware stack. This stack is outside the PIC’s normal memory map, so its contents cannot be altered by any normal process.4

Associated with this stack is a 3-bit counter which points to the next available register in the stack. This Stack Pointer (SP) cannot be explicitly altered by any instruction but it is automatically incremented each time a call instruction is executed. call is similar to a goto instruction, but before the specified instruction address is put into the Program Counter the current value of PC is pushed into the stack. This is the address of the instruction after the call instruction, as the PC has already been

3The 12-bit core devices have only two 11-bit stack registers and the 16-bit core PICs have a 16-deep stack.

4Most MPU/MCUs use an area of normal RAM together with a dedicated address register to implement their stack. This is much more flexible than a dedicated hardware stack but needs a more complex instruction set to manipulate the Stack pointer and to push and pull/pop data into and out of the stack.

6. Subroutines and Modules 141

incremented and the PIC is fetching this next instruction into the pipeline at the same time as the call instruction is being executed – see Fig. 4.4 on page 87.

(a) Before

Fig. 6.3 Using the hardware stack hold return addresses.

In Fig. 6.3(b) the situation is shown after a call to a subroutine labelled DELAY_100MS. The execution sequence of this call DELAY_100MS is:

1.Copy the 13-bit contents of the PC into the stack register pointed to by the Stack Pointer. This will be the address of the instruction following the call instruction.

2.The Stack Pointer is decremented.

3.The destination address DELAY_100MS, that is the location of the entry point instruction of the subroutine, overwrites the original state of the PC. E ectively this causes the program execution to transfer to the subroutine.

Apart from the pushing of the return address into the stack in steps 1 and 2, call acts exactly like a plain goto. Thus call requires two bus cycles for execution as the pipeline needs to be flushed to remove the next caller instruction which is already in situ. This similarity also applies to the extension of its 11-bit absolute address in the call instruction word to a 13-bit Program store address using bits 3 & 4 of the PCLATH register, as shown in Fig. 5.4 on page 114. Far calls to subroutines located between

6. Subroutines and Modules 143

path. This pattern is matched by the last-in first-out (LIFO) structure of the stack mechanism, which can handle any arbitrary nesting sequence to any depth of eight subroutines automatically. It can even handle the (painful) situation where a subroutine calls itself! Such a subroutine is known as recursive. As we shall see in the next Chapter 7, the stack mechanism is also used to handle interrupts. Thus, in a system using both subroutines and interrupts the nesting depth will be somewhat less. The technique is so useful that virtually all MPU/MCUs support subroutines in this manner.

As the stack-Stack Pointer mechanism is part of the PICs hardware and requires no initialization, from the programmer’s perspective only the following points are relevant:

•The subroutine should be invoked using the call instruction.

•The entry point to a subroutine should be labelled, and this label is then the name of that subroutine.

•The exit point from the subroutine should be either return or retlw, with the latter being used when a known constant is to be in the Working register on return – see Program 6.4.

As an example, let us code the 0.1 second (100 ms) delay subroutine of Fig. 6.2. Creating a delay in software is simply a matter of doing nothing for the appropriate duration. A common way of doing this is to count down an initial constant to zero. By choosing an appropriate constant, the delay can be tailored to the desired value. Obviously, this delay will depend on the PIC’s oscillator rate. For the examples in this chapter we will assume a clock rate of 4 MHz, giving a bus cycle of 1 µs.

Consider the single-byte count code fragment:

This continually decrements the initial setting N of the register file labelled COUNT, dropping out when it reaches zero. The total delay is contributed by both instructions as:

1.The decfsz takes one cycle to execute, except when N reaches zero, in which case two cycles are needed as the pipeline needs to be flushed

– see page 127. This gives a total execution time of [(N −1) ×1] +2.

2.As the loop exits by skipping over the goto instruction, this is only executed N − 1 times; each time taking two bus cycles. This contribution is thus (N − 1) × 2.

6. Subroutines and Modules 147

that a subroutine should disturb its environment as little as possible. DELAY_K100MS is not very good in this respect, using three file registers for its internal use and altering the Working register. As an example of what could go wrong, Program 6.3 shows an implementation of the task list but calling the 100 ms block as the existing Program 6.1 subroutine; that is a nested subroutine. Here File 30h is used as a store for K oblivious to the fact the this register file is used by subroutine DELAY_100MS as one of its counters. The e ect of this interaction is to make K zero on return from DELAY_100MS, which when decremented at Task 2 will always give a non-zero outcome. Thus the delay is infinite and the system locks up! Simply changing K equ 30h to K equ 32h fixes the problem; but if another member of the team with responsibility for the DELAY_100MS subroutine alters its internal storage map without communicating this to other team members then catastrophe may occur! Thus even though each subroutine could have been passed when tested on its own, certain combinations of calling sequences could cause failure. We will return to this problem later.

Program 6.2 is still void in that no data was returned to the caller on exit. For our next example we will code a subroutine that will activate a decimal readout. Many numeric electronic displays are based on a selective activation of seven segments in the manner shown in Fig. 6.6.

Program 6.3 An alternative K × 100 ms delay subroutine.

; ************************************************************

; Task 1: DO 100ms delay DK_LOOP call DELAY_100MS

; Task 2: Decrement K

6. Subroutines and Modules 149

Table 6.2: The 7-segment lookup table showing byte[N] being extracted.

Although this approach does work, there are limitations. Any alteration of the PCL register will cause both these eight bits together with the lowermost five bits of the PCLATH to be moved into the 13-bit PC

– as described in Fig. 4.3 on page 86. This means that if the instruction addwf PCL,f causes the 8-bit PCL to overflow or if the contents of the PCLATH does not match the upper bits in the full PC, then the outcome stored into the PC will not be as the programmer wished – see Example 6.7. This is not easy to check, as the programmer is unlikely to know in advance where the subroutine is located in memory, that is what value the PC will have at the beginning of the subroutine. Even if he/she checks the assembler listing file (see Table 8.1 on page 206) for the value of SVN_SEG, this can change if subsequent alterations are made to other parts of the

Program 6.4 The software 7-segment decoder.

150 The Quintessential PIC Microcontroller

program. It is possible to devise code to allow this address boundary to be crossed, but at the expense of complexity – see Example 6.7. The Microchip application note AN556 Implementing a Table Read gives techniques for dealing with these problems.

The code in Program 6.4 takes no account of the possibility that the datum in W is greater than 09h. Of course it shouldn’t be, but robust code should cope with all contingencies even if it is technically erroneous. This is especially true if the code module is to be reusable for general-purpose applications. What would happen if this situation arose and how could you add to the code to gracefully return an error code, say −1, in this eventuality?

Using W to transfer information to and fro a subroutine is limited to a single byte datum each way. Where several pieces of information of byte or greater sizes are to be passed, then file registers must be pressed into service for this conduit. An example of this is shown in Program 6.5 where two byte datums, labelled MULTIPLICAND and MULTIPLIER are to be multiplied giving a 16-bit outcome labelled PRODUCT_L:PRODUCT_H.

Fig. 6.7 System diagram for the byte multiplication subroutine.

The principle of the multiplication algorithm coded in Program 6.5 is a generalized version of that used by previous multiplication routines, such as Program 5.11 on page 133. Here the multiplier ten was decomposed to ×2+×8 which could be implemented by shifting once and three times respectively. In the more general case the multiplicand is shifted left and the nth shifted word added to the product if bit n of the multiplier is 1. Doing this eight times gives:

7

Product = (multiplicand<<n) × bit n

n=0

where the << operator denotes shift left.

Using this shift and add algorithm gives the task list:

1.Zero double-byte product.

2.Extend Multiplicand to 16 bits.

3.DO

(a)Shift Multiplier right once.

6. Subroutines and Modules 151

(b)IF Carry bit is one THEN and Multiplicand to subproduct.

(c)Shift Multiplicand right once.

(d)Repeat WHILE product not zero.

4.End with 16-bit Product.

Program 6.5 declares the variables that are passed to and from the subroutine at the of the main program. Keeping all these global declarations in one part of the program and using a di erent file register for each overall global variable reduces the possibility of interaction but at the expense of rather extravagant use of scarce Data memory resources. Temporary local storage is declared within each subroutine as its need will be ‘thrown away’ after the subroutine is terminated. However, interaction can still occur in local storage where nested subroutine structures are used.

The coding follows the task list closely. The decision whether to add the left-shifted multiplicand to the subproduct is dependent on the state of the Carry flag when the multiplier is shifted right. This implements the conditional addition

product = product + (multiplicand<<n) × bit n

Rather than implementing this shift and conditional add process eights times, the summation loop is terminated whenever the multiplier residue is zero. This means that the execution time of the subroutine is variable, depending on the bit pattern of the multiplier. The worst-case scenario is when the multiplier is 255 (11111111b). This takes 142 cycles including the two cycle call.

In order to use this subroutine, the caller copies the multiplicand into File 20h and multiplier into File 21h. On return, the 16-bit product can be read at File 2E:Fh. As an example, consider that the bytes located at File 42h and File 46h are to be multiplied.

Most MPU/MCUs have software stacks which in addition to saving subroutine return addresses allow the programmer to push and pull data to and from memory to pass information between caller and subroutine. As the stack is a dynamic storage entity, growing where necessary to accommodate these passed and temporary variables and shrinking again when the subroutine terminates, this clearly is an e cient method of memory allocation. Furthermore, each call outwards in a nested structure opens a new stack frame for this dynamic storage as an extension to the

152 The Quintessential PIC Microcontroller

Program 6.5 The byte multiplication subroutine.

;The MULT subroutine

;************************************************************

;************************************************************

;Local declarations

MULTIPLICAND_H equ 30h

; Task 1: Zero double-byte product MUL clrf PRODUCT_L

clrf PRODUCT_H

; Task 2: Extend multiplicand to 16 bits clrf MULTIPLICAND_H

;Task 3: DO

;Task 3A: Shift multiplier right once

6. Subroutines and Modules 155

(b)Copy the Multiplicand from memory (we assume it is at File 46h as in our last example) into W and then indirectly into the frame using INDF as the target. Decrementing the FSR completes the push action.

(c)In a similar manner, the Multiplicand is pushed into the stack.

(d)Call the subroutine.

Coding of the subroutine MUL_S is given in Program 6.6. This implements items 2–4 of Fig. 6.8. Firstly, MULTIPLICAND_H, the temporary storage of the multiplicand overflow, is zeroed and then zero is pushed into the next two locations to create the initial value for the product. In item 4 the Pseudo Stack Pointer is reset to point to the next free byte below the frame. In this way, should the subroutine wish to call another, then there will be a new frame available for that next-level storage with the new TOF beginning just below the old frame. These two instructions may be omitted in this case as there are no further nested call outs, although Task 3C will have to be altered. This is done in Example 6.6.

The core of the subroutine, that is Task 3, is similar to Program 6.5 but the FSR has to be moved up and down the frame to access the appropriate level. The only non-obvious use of the FSR is at Task 3C. As there are two ways into this routine, depending on whether the shifted multiplicand is added to the product or not, the state of the FSR is unknown. It can however be reset from the PSP which is pointing to just below the frame at this point. By adding five to this PSR value, the FSR will always point to MULTIPLICAND.

Finally the subroutine ‘cleans up’ the stack by updating the Pseudo Stack Pointer to its previous value. In this case this is done by adding five, but in general by adding the frame depth n.

Program 6.6 requires 45 instructions as compared to 20 in Program 6.5. Its worst-case execution time of 274 cycles also compares unfavorably

156 The Quintessential PIC Microcontroller

with 142 cycles. Thus in all respects except reusability and robustness this stack-based model is clearly inferior. It may be more economical in

Program 6.6 Implementing a byte multiply using a stack model. (continued next page).

; ************************************************************

;************************************************************

;Tasks 1 & 2: Extend multiplicand and zero double-byte product

;Task 3: DO

;Task 3A: Shift multiplier right once

; Task 3B: IF Carry == 1 THEN add multiplicand to product btfss STATUS,C ; IF C == 1 THEN do addition

goto MUL_CONT ; ELSE skip this task

6. Subroutines and Modules 157

Program 6.6 (continued.) Implementing a byte multiply using a stack model.

its use of scarce data memory in large software systems. However, in programs running on low and mid-range PICs are often not very complex. Furthermore the small Program memory (1024 instructions for the PIC16F84) may further restrict the use of this relatively extravagant technique. Where real-time execution time is critical the additional burden of stack handling is unlikely to be worthwhile.

Examples

Example 6.1

The binary series approximation to the fraction 13 is:

1 1 1 1 1 1 1 1 3 = 2 − 4 + 8 − 16 + 32 − 64 + 128 · · ·

Using this series, write a subroutine that will divide a byte in the Working register by three with the quotient being returned in the same W register. The actual value of the summation up to 1281 is 0.3359375, which is within 0.78% of the exact value. With an 8-bit datum there is no point in including any further elements in the series, but where 16-bit operands are being processed then further elements up to the desired accuracy can be summed in the same manner.

158 The Quintessential PIC Microcontroller

Solution

The fractions 12 , 14 , 18 etc. can be easily generated by shifting right. The coding listed in Program 6.7 simply repetitively shifts the number as copied to a temporary location in register file File 33h right. Notice that it is necessary to clear the Carry flag before each shift as both the previous Rotate and Subtract instructions can alter its state. As the subwf instruction subtracts the contents of W (the sub quotient) from the datum in the specified file register then the outcome being built up in W will oscillate in sign as desired. In situations where the series element signs

Program 6.7 Dividing by three

; ************************************************************

;************************************************************

;Local declarations

160 The Quintessential PIC Microcontroller

Solution

For a delay as long as this we need to extend Program 6.1 to use a larger count. In the coding of Program 6.9 three file registers are used to give a triple loop.

File register COUNT2 is initialized to the value H whilst the other two file registers are cleared giving an e ective count range of 256. The outer loop exits the program when COUNT2 reaches zero. This single pass therefore contributes (H × 3) − 1 cycles to the total delay. Each pass through the COUNT1 loop takes (256 ×3) −1 cycles and there are H passes giving a contribution of H × [(256 × 3) − 1] cycles. In the same manner the inner loop based on decrementing COUNT0 runs H × 256 times each pass contributing (256 × 3) − 1 cycles to the total. Thus we have a total delay of:

(H × 3) − 1 + H × [(256 × 3) − 1] + H × 256 × [(256 × 3) − 1] + 6

Equating this to 106 ( µs per second) gives H ≈ 5. The actual delay with an H of 5 is 0.985615 s which is accurate to 1.4%. If desired the shortfall of 14,385 cycles can be made up by adding nop instructions to the middle count loop. Each such instruction gives an extra 1280 cycles. The

Program 6.9 A 1-second delay program.

; *************************************************************

; *************************************************************

DELAY_1_S movlw movwf clrf clrf

D_LOOP

decfsz goto decfsz goto decfsz goto return

6. Subroutines and Modules 161

maximum delay possible with this program is 50.46 s for H = 0 (e ectively 256).

Example 6.4

Design a subroutine to convert a binary byte passed in W to a 3-digit BCD equivalent in HUNDREDS (File 30h), TENS (File 31h) and UNITS (File 32h).

Solution

We have already coded a routine to implement this mapping in Example 5.3 on page 129. However this was restricted to a range 0–99, that is two digits. Nevertheless we can extend the technique used there by first subtracting and counting hundreds from the original binary byte. After this has been computed then the residue will be less than 100 and the rest of the coding will be the same, as shown in Program 6.10. Thus a suitable task list would be:

1.Divide by 100; the remainder is the hundreds digit.

2.Divide the quotient by ten; the remainder is the tens digit.

3.The quotient is the units digit.

Program 6.10 Binary to 3-digit BCD conversion.

;************************************************************

;* FUNCTION: Converts a binary byte in W to three BCD digits*

;************************************************************

;First divide by a hundred

6. Subroutines and Modules 163

root. An example giving √65 = 8 is given in Fig. 6.9(a) using this series approach. A flowchart visualizing the task list is also given in Fig. 6.9(b).

Program 6.11 Coding the square root subroutine.

;************************************************************

;* FUNCTION: Calculates the square root of a 16-bit integer *

;************************************************************

;Local declarations

;Task 3: DO

;Task 3(a): Number - I

; Task 4: Return loop count as the square root

SQR_END movf COUNT,w ; Copy into W return

164 The Quintessential PIC Microcontroller

The coding in Program 6.11 follows the task list closely. The maximum value of the loop count is FFh, as √65535 = 255. Thus a single byte at File 35h is reserved for this local variable. Similarly the maximum possible value of the magic number is 511 (1FFh) and so the two registers File 36:7h are reserved for this local variable. This of course means that Task 3(a) entails a double-byte subtraction. The coding is somewhat simplified as the high byte of I, that is I_H, is never more than 01h and so a borrow from the lower byte can be added to a copy of I_H before the high-byte subtract to return the borrow without overflow. If a borrow is generated from this high-byte subtraction the outcome is under zero and the loop is exited. Otherwise COUNT is incremented and I augmented by two. Actually the latter is always twice COUNT plus one, so COUNT is not needed. Instead, on return the 16-bit value I can be shifted once right. This divides by 2 and by throwing away the one that pops out into the carry, e ectively subtracts by one – I is always odd and so its least significant bit is always 1. Try coding this alternative arrangement.

Example 6.6

Repeat Example 5.5, which multiplies a byte by ten, but using a software stack for data storage and parameter passing. You may assume that the multiplicand byte is in memory at File 46h.

Solution

The global declarations for the subroutine of Program 6.12 and calling procedure is:

;..........................and so on

;Get ready to call up the X10 subroutine

movf PSP,w ; 1st point to current stack position

call X10 ; Now call subroutine

;On return PSP is returned to original position

;and product is at PSP+3:PSP+2

NEXT_MAIN ..... ... ; Continuation of main routine

6. Subroutines and Modules 165

Program 6.12 uses the same technique as the original routine. First the multiplicand is shifted left once to multiply by two and then two further shifts multiplies by eight. The two resulting 16-bit data are then added to give the product. In the same manner as Program 6.6, the File Select Register is moved up and down to point the the appropriate datum as the

Program 6.12 Using a software stack to pass parameters and to provide a workspace. (continued next page).

;************************************************************

;* FUNCTION: Xs byte XCAND by 10 giving double-byte product *

; ************************************************************

166 The Quintessential PIC Microcontroller

Program 6.12 (continued.) Using a software stack to pass parameters and to provide a workspace.

return

; ************************************************************

program progresses. The double-byte product can be accessed relative to the Pseudo Stack Pointer by the caller. Unlike Program 6.6 this PSP is not altered when pushing out the multiplicand nor in the subroutine. This is because the subroutine is a dead end in that it can never call another subroutine. Thus a new stack frame need not be formed.

Example 6.7

In order to ensure that the 7-segment decoder subroutine of Program 6.4 does not cause the PCL register to overflow when the o set is added, a programmer has used the directive org (ORiGin – see page 200) to tell the assembler to locate the subroutine at the absolute instruction address 700h – as shown in Program 6.13. When the subroutine is tested by calling from another part of the program in the store somewhere lower than 700h the system fails and performs unpredictably. What has gone wrong?

Program 6.13 The software 7-segment decoder revisited.

6. Subroutines and Modules 167

Solution

The system goes berserk because on reset the PCLATH register is zeroed. Summoning the subroutine using call 700h the value of the PC becomes 0700h but the value of the PCLATH register remains unaltered. Later when the addwf PCL,f instruction is executed the full 13-bit Program Counter is updated with the bottom eight bits from the PCL register and the top five bits from the PCLATH register – as described in Fig. 4.3 on page 86. Thus instead of the execution branching to one of the retlw instruction it will jump somewhere in Program memory in the area 0000

– 00FFh! This will happen even though adding the o set in W will not cause overflow of the PCL register, as was the original intention.

One way of avoiding this error would be to set the PCLATH to page 7 prior to the call, thus causing the Program Counter to be advanced to location 07NNh as desired instead of 00NNh.

Even with this kludge the table is limited to 254 entries before the addition overflows the PCL register causing a malfunction. In any case it is considered bad practice for the programmer to specify the absolute location of sections of program code, as it is possible to overwrite code that the assembler places itself. Anyway with large programs it is error prone to try and keep tabs on the location of a myriad of modules. One way around the problems of both large tables and ensuring that the PCLATH register is correctly set, is for the caller to calculate the proper addition of the 13-bit value of the beginning of the subroutine SVN_SEG to the o set and place the top byte of the outcome in the PCLATH register. Of course the PIC is only capable of doing 8-bit arithmetic at a time and so we need to be able to find the values of both the bottom and top bytes of the label SVN_SEG. Fortunately the Microchip assembler has the directives high and low which can be used to dismember a 13-bit address to facilitate address arithmetic.

168 The Quintessential PIC Microcontroller

In the code segment above the address of the start of the table; that is SVN_SEG+1 is used, as this will be the value of the PC after the opening addwf PC,f instruction. Of course the org 700h instruction used in Program 6.13 can be dispensed with.

This code segment can easily be extended to deal with o sets which are greater than one byte by doing a double-byte addition to update PCL. As before only the lower byte of the o set is sent to the subroutine. In this way look-up tables of any size and located anywhere in Program memory can be implemented subject to the limited size of the Program store.

Self-assessment questions

6.1Improve the accuracy of the 1-second delay Program 6.9 to within 0.2% by inserting nop instructions into strategic parts of the coding.

6.2Create a subroutine that will read Port B every hour. You can base it on a 30-second version of Program 6.9. Say why this may not be a good use of the PIC’s resources.

6.3Code a subroutine with the following specification:

•To divide a double-byte dividend by a byte divisor.

•Input DIVIDEND_H:DIVIDEND_L to be passed in File 2E:Fh.

•Input Divisor to be passed in the Working register.

•Output QUOTIENT_H:QUOTIENT_L to be returned in File 29:Ah.

•Output Remainder to be returned in W.

Use the subtract until underflow algorithm of Example 3.3 on page 67. Comment on the problem of doing this division in this way.

6.4Extend Program 6.4 to display A through F. Your solution can use a combination of lower and upper-case glyphs and should be robust.

6.5Readings of the state of a mechanical switch can be erratic as the contacts will bounce for several milliseconds when closed, thus giving a series of 1s and 0s. Similar considerations apply to electronic devices such as phototransistors when passing through a shadow. Although this problem can be fixed with hardware, it is usually more cost e ective to use a software solution.

Devise a subroutine that will return with the stable state of a switch connected to Port B bit 7 as bit 7 of the Working register. Stability is defined as 5000 (1388h) reads all giving the same value. The other bits of W are undefined.

6. Subroutines and Modules 169

6.6An analog to digital converter is connected to Port B. Repeat SAQ 6.5 but this time defining stability as 1000 identical reads, and returning with the stable digitized analog voltage in W.

6.7The subroutine in SAQ 6.6 returns the stable value of a noisy digitized signal, assuming 1000 identical values. Using this subroutine, code a main routine that will generate how this stable reading di ers from a previous value previously stored in location File 40h. Each bit that di ers is to be logic 1. Generate the position of the rightmost change bit in File 41h.

6.8The subroutine of SAQ 6.6 will not return a value when relatively high-frequency noise is present on the analog signal, as the resulting digital jitter will ensure that 1000 identical readings rarely occur. As an alternative, noise reduction can be obtained by taking the average

of multiple readings. If the noise is random then n readings will give a noise improvement of √n. Devise a subroutine that will read Port B 256 times and return the 8-bit average in W for an increase in signal to noise ratio of 16.