Genomics and Proteomics Engineering in Medicine and Biology - Metin Akay

184 ERROR CONTROL CODES AND THE GENOME

non-protein-coding, regulatory regions that control translation initiation, which is typically the rate-limiting aspect of the protein production process [32, 38, 39]. Given the importance of regulating protein synthesis and the redundancy present in regulatory regions such as the ribosome binding site (RBS), it seems plausible that regulatory information is error control encoded [40].

7.3. REVERSE ENGINEERING THE GENETIC ERROR CONTROL SYSTEM

The information produced by genome projects is key to understanding how an organism functions from geneticto cellular-level behavior. Identifying gene locations and regulatory regions is a fundamental step in this process. It is not feasible to experimentally annotate all of an organism’s regulatory regions—hence the need for computational tools for accurately deciphering the information contained in genetic sequences. The majority of gene annotation techniques rely on patterns and statistical characteristics of the genome for model construction. While these methods yield viable results, they do not offer insight into the underlying mechanics of the genetic process.

Coding theory algorithms can serve as powerful pattern recognizers for annotating biologically active sites of a genome and also as pattern generators that can mathematically represent the genetic process and macromolecules that operate on a genomic sequence of interest. The mathematical representation of a convolutional code is also the mathematical model for the digital system that produces that signal (or pattern) and all other signals associated with that system.

Development of coding-theoretic frameworks for molecular biology is an ongoing endeavor. Although the existence of redundancy in genetic sequences is accepted and the possibility of that redundancy for error correction and control is being explored and exploited, mathematically determining the encoding algorithm, particularly for regulatory regions, remains a major research challenge. Devising a method for reconstructing the error control code of a received, noisy signal is a challenge that if met will provide a way to construct mathematical models of molecular machines (macromolecules such as ribosome, RNA polymerase, and initiation factors) involved in the regulation of genetic processes. Reverse engineering the genetic ECC system requires thorough investigation of several issues, including:

1.Is there plausible and potentially quantitative evidence that ECC exists in genomic sequences.

2.What are the ECC characteristics of the genetic system (characteristics that parallel traditional communication systems such as channel capacity and coding rate)?

3.Assuming the existence of some type of genetic ECC, how can we computationally invert the system using potentially noisy sequence information?

7.3.1. Making a Case for Existence of Error Control in Genomic Sequence

Several researchers have moved beyond the qualitative models of biological communication and attempted to determine the existence of error control codes for genomic sequences [20, 31, 34, 41, 42]. Liebovitch et al. [41] and Rosen and Moore [34] both developed techniques to determine the existence of an error control code for genomic sequences. Neither found evidence of error control codes for the sequences tested. Given the computational limitations of the study, Liebovitch et al. suggest that a more comprehensive examination would be required. Both methods investigate a subset of linear block codes and do not consider convolutional coding properties or account for the inherent noise in genomic sequences. Extending beyond specific genomic regions and sequences, MacDonaill develops an ECC model for nucleic acid sequences in general [42]. He has proposed a four-bit, binary, parity-check error control code for genetic sequences based on chemical properties of the nucleotide bases.

Battail presents a more qualitative argument supporting the potential existence of a genetic error control system [30]. He argues, similar to Eigen [21], that for Dawkins’s model of evolution to be tractable, error correction or ECC must be present in the genetic replication process. According to Battail, proofreading, a result of the error avoidance mechanism suggested by genome replication literature, does not correct errors present in the original genetic message. Only a genetic error correction mechanism can guarantee reliable message regeneration in the presence of errors or mutations due to thermal noise, radioactivity, and cosmic rays [30].

Battail further asserts that the need for error protection becomes obvious when one considers that the number of errors in a k-symbol message that has been replicated r times is comparable to the number of errors in an unreplicated (r k)-symbol message. For a given error rate, the number of times an organism undergoes replication approaches an infinite number. Hence for a message to remain reliable within an organism’s life cycle (not to mention evolutionary information transmission which occurs over thousands of years), the message must have strong error protection. Battail points out that if there exists a minimum Hamming distance d between codewords, then almost errorless communication is possible if and only if the following holds:

where p is the error probability for the channel and n is the length of the codewords. If we take n to be the length of the gene or a portion of the gene, minimum-distance decoding may be used to produce a near errorless rule [30]. Eukaryotes’ tendency to evolve toward increasing complexity may parallel the connection between increasing word length and increasing reliability, which is stated in the fundamental theorem of channel coding [30]. The fundamental theorem of channel coding states that coding rates that are below the channel capacity result in arbitrarily small probabilities of error (ln ! 0) for sufficiently large blocks lengths n [43].

186 ERROR CONTROL CODES AND THE GENOME

FIGURE 7.5. Binary (7, 4) block code.

Taking a unique approach to the question of error control codes in genomic sequences, Schmidt and May [44] exploit graph-theoretic methods in their investigation of ECC properties of Escherichia coli K-12 translation initiation sequences. They discover that unlike binary random sequences, binary block codes form distinctive cluster graphs (see Figs. 7.5 and 7.6). Applying this graph-based method to a subset of E. coli K-12 initiation sites, they observe that while noninitiation sites fail to cluster into distinct groups (Fig. 7.7), there is evidence of cluster formation in valid initiation sequences (Fig. 7.8), suggesting the possibility of ECC-type characteristics for E. coli translation initiation sites.

7.3.2. System Characteristics

The capacity of the communication channel is a key system characteristic that governs the type of ECC used in transmission. The genetic communication system depicted in Figure 7.4 represents the error-introducing transmission

FIGURE 7.6. Binary random sequence.

channel as the replication process. Shannon’s channel coding theorem asserts that there exists a channel code with rate R ¼ k=n such that the probability of decoding error becomes arbitrarily small as n increases [4, 23, 43]. The capacity of a transmission channel (the maximum data transmission rate) is dependent on the error rate of the channel pi, j, the probability of the channel transforming symbol i into symbol j for i = j. In order to determine appropriate ECC parameters for genetic regulatory sequences, we must characterize the replication channel and the error or mutation rates associated with replication. Mutation-derived capacity values can suggest R and from that plausible n and k values for genetic systems.

Mutations are replication errors that remain or are missed by genetic proofreading mechanisms. Drake et al. [45–47] have performed extensive research and analysis of mutation rates in prokaryotic and eukaryotic organisms. Based on mutagenesis studies, they note that mutation rate in RNA viruses range from 1 per genome per replication for lytic viruses to 0.1 per genome per replication for retroviruses and retrotransposons. The DNA microbes, more complex and

188 ERROR CONTROL CODES AND THE GENOME

FIGURE 7.7. Graphical representation of ECC properties of E. coli K-12 noninitiating intergenic regions.

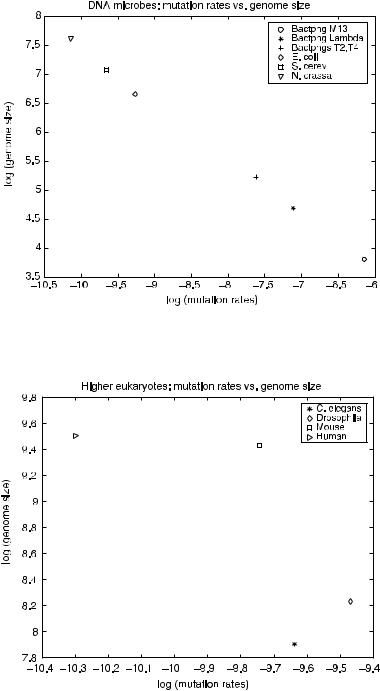
typically larger than RNA viruses, have mutation rates of 3001 per genome per replication. Moving higher still to the larger, more complex eukaryotic organism, higher eukaryotes have mutation rates ranging from 0.1 to 100 per genome per sexual generation and a mutation rate of 3001 per cell division per effective genome. The effective genome is the portion of the genome where mutations are most lethal (i.e., genes or exons) [45]. In general, while RNA viruses have significantly higher mutation or channel error rates, DNA microbes have error rates relatively similar to the mutation rate in the effective genome of higher eukaryotes. The question arises whether and how organism complexity (which we can loosely approximate using genome size) is related to replication channel fidelity. Drake investigates this for DNA microbes by analyzing the log-log plot of base mutation rates as a function of genome size [46]. These plots are reproduced using the base mutation and genome size data from Drake et al. [45] for both the DNA microbes and the higher eukaryotes.

FIGURE 7.8. Graphical representation of ECC properties of E. coli K-12 translation initiation sites, position 210 to 23.

Figures 7.9 and 7.10 show the log-log plots of genome size as a function of base mutation for DNA microbes and eukaryotic organisms, respectively. The log-log plots for the DNA microbes are equivalent to Drake et al.’s results, as would be expected. The relationship between the DNA microbes’ mutation rates and genome size exhibits power law behavior. Higher eukaryotes do not appear to exhibit

in Figure 7.9, there is an inverse relationship between genome size G and an organism’s base mutation rate mb. This inverse relationship is evident for the higher eukaryotes as well.

The genetic channel capacity is calculated using mutation rates reported in Drake et al. [45]. Assuming a discrete memoryless channel (DMC), the capacity of the channel, C, is the maximum reduction in uncertainty of the input X given knowledge of Y [43]:

The probability p( yj j xk) is the channel error probability. If p( y j x) is specified by the

mutation error rate mb, then p( yj j xk) ¼ mb 8y = x and p( yj j xk) ¼ 1 mb 8y ¼ x (where mb is the mutation rate per base per replication). The channel transition

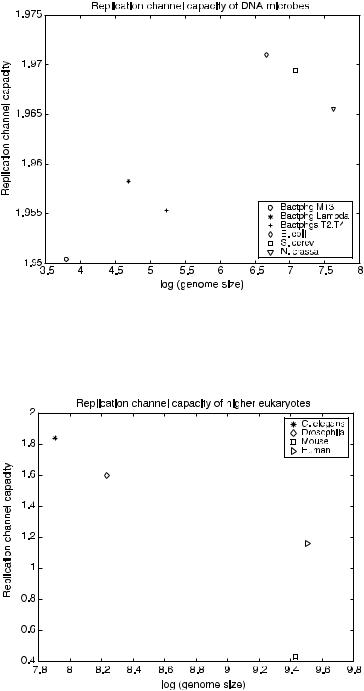
matrix (Table 7.2) assumes all base mutations are equal; hence a transition mutation [purine to purine, adenine(A) ! guanine(G), and pyrimidine to pyrimidine, cytosine(C) ! thymine(T)] and a transversion mutation [purine to pyrimidine, (A, G) ! (C, T), and pyrimidine to purine, (C, T) ! (A, G)] are equally probable. Additional capacity calculations are being performed using transition probability matrices where the probability of a transition mutation is greater than the probability of a transversion mutation, which is consistent with the biological evidence. Figures 7.11 and 7.12 show the replication channel capacity of the organism as a function of the log of the organism’s genome size for DNA microbes and higher eukaryotes, respectively, using mb values from Drake et al. [45] and channel transition probabilities from Table 7.2. The prokaryotic organisms have larger channel capacity than the higher eukaryotes. This suggests that for DNA microbes the coding rate R is closer to (n 1)=n, leaving few bases for ECC. In contrast, the channel capacity values for higher eukaryotes implies a distinctly smaller value for R. This implies that the eukaryotic genome has more bases available for ECC.

7.3.3. Inverse Error Control Coding Models

If the encoding algorithm for a received error-control-encoded sequence is unknown or part of the data are missing, designing a viable decoder for the received transmission is a significant but rarely addressed computational challenge. Communication engineers forward engineer ECC systems and do not encounter this situation often. In order to determine the ECC properties of genetic systems and the algorithm used by living systems to transmit vital genetic information, researchers are developing quantitative approaches to reverse engineering error-control-encoded data streams and genetic sequences.

7.3.3.1. Inverse ECC Model I: Ribosome as Block Decoder May et al. [48, 49] modeled mRNA as a noisy, systematic zero-parity encoded signal and the ribosome as an (n, k) minimum-distance block decoder (where the 16S ribosomal RNA is used as a template for generating all valid n-length codewords). The model was able to distinguish between translated sequence groups and nontranslated sequence groups from E. coli K-12 genome. When applied to mRNA leader regions of other prokaryotic organisms (Salmonella typhimurium LT2, Bacillus subtilis, and

Staphylococcus aureus Mu50), similar results were observed.

The original block code model was developed based on the last 13 bases of the 30 end of 16S ribosomal RNA [32] and consisted of a set of 33 and 26 codewords for the (5,2) and (8,2) codes, respectively. The codewords were constructed using heuristics based on RNA/DNA base-pairing principles and common features of bacterial ribosomal binding sites (such as the existence and location of the Shine–Dalgarno sequence). Although the original model can be used to distinguish between valid and invalid leader sequences, a deterministic representation would provide a quantitative model of the translation initiation system that can be used to algorithmically correct errors in the system and generate plausible leader sequences.

Toward this end, we revisit the algorithmic structure of linear block codes, previously described in Section 7.1.2. Each codeword v in an (n, k) linear block code’s codebook can be produced using a generator matrix G, which encodes the information vector u in a deterministic manner [25]. Recall the relationship

where G is k n, u is 1 k, and v is 1 n. The parity-check matrix H is a (n k) n matrix and relates to the generators as follows [23, 25]:

where HT is the transpose of the parity-check matrix. The parity-check matrix is used to check for transmission errors in the received sequence, r ¼ v þ e as previously discussed. In the absence of errors, e ¼ 0, the syndrome vector s will be an