
Konspekt_OTN
.pdf2.1.3. Вероятность безотказной работы в течение заданного интервала наработки
Рассмотрим два интервала наработки (0, t1) и (t1, t2). Вероятность без-
отказной работы на интервале (0, t2) определяется совместным появлением двух событий:
объект безотказно проработал на интервале (0, t1), вероятность пер-
вого события P(t1);
оставшийся работоспособным к моменту t1 объект безотказно про-
работал на интервале (t1, t2), вероятность второго события P(t1, t2). По правилу умножения вероятностей (прил. 1)
P t2 P t1 P t1,t2 .
Следовательно, |
|
P t1,t2 P t2 /P t1 . |
(1.3) |
2.1.4. Плотность распределения наработки до отказа
Плотность распределения наработки до отказа является дифферен-
циальной формой закона распределения наработки до отказа (прил. П.2)
q t |
dQ t |
|
dF t |
, |
(1.4) |
dt |
|
||||
|
|
dt |
|
||
|
|
причем, |
q t dt 1. |
|
0 |
В соответствии с известными соотношениями (прил. 2) функция надежности и функция ненадежности связаны с плотностью распределения наработки до отказа уравнениями:
t
F t 1 q x dx q x dx,
0 t t
Q t q x dx .
0
2.1.5. Интенсивность отказов объекта
Величина q(t)dt характеризует вероятность отказа за интервал наработки (t, t + dt) объекта, взятого наугад из множества одинаковых объектов. При
13
этом неизвестно, работоспособен ли этот объект к началу интервала или отказал ранее. Это не всегда удобно на практике. Поэтому чаще применяют другой показатель - интенсивность отказов. Это условная плотность вероятности возникновения отказа невосстанавливаемого объекта, определяемая для заданной наработки при условии, что до этой наработки отказ не возник. Интенсивность отказов можно рассматривать как относительную скорость уменьшения значений функции надежности с увеличением интервала наработки. При использовании показателя "интенсивность отказов" рассматриваются лишь остающиеся работоспособными к моменту t объекты, а отказавшие исключаются из рассмотрения.
|
|
|
q |
|
|
|
|
|
|
|
/dt |
|
||
t |
t |
|
|
dF t |
|
|
||||||||
|
|
|
|
|
. |
(1.5) |
||||||||
F t |
|
|
F t |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение этого уравнения при начальном условии F(0) = 1 дает для |
||||||||||||||
функции надежности формулу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
(1.6) |
||||||
F t |
|
exp |
|
|
x dx . |
|||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||
2.1.6. Средняя наработка до отказа
Средней наработкой до отказа объекта называется математическое ожидание наработки объекта до отказа:
|
|
dQ t |
|
|
T t q t dt t |
|
dt. |
(1.7) |
|
dt |
||||
0 |
0 |
|
|
|
Используя известные соотношения между формами представления закона распределения (прил. 2) можно записать
|
|
T F t dt. |
(1.8) |
0 |
|
Средняя наработка объекта до отказа есть площадь под кривой вероятности безотказной работы.
Перечисленные выше показатели надежности могут быть найдены разными способами в зависимости от типа расчета надежности - параметрического или непараметрического. Ниже рассмотрим несколько моделей отказов, опирающихся на оба из них.
14
Лекция №3
3. МОДЕЛЬ ОТКАЗА: НАГРУЗКА И ПРОЧНОСТЬ - СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
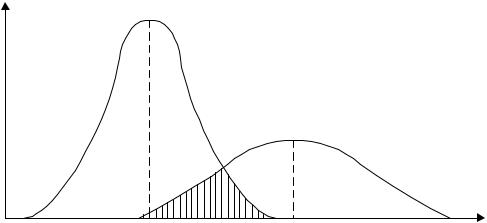
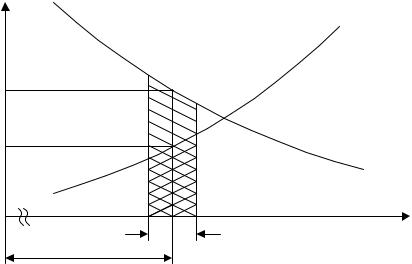
Обозначим через fп(x) - плотность распределения прочности, а через fн(x) - плотность распределения нагрузки (Рис. 1.1, а). Отказ наступает тогда, когда случайная величина прочности окажется меньше случайной величины нагрузки. Заштрихованный участок показывает область перекрытия распределений нагрузки и прочности, которая характеризуется определенной вероятностью отказа. Изобразим эту область в увеличенном масштабе, чтобы рассмотреть ее более детально (Рис. 1.1, б).
Предположим, что нагрузка находится в небольшом интервале dx
вблизи x0. Обозначим вероятность этого события fн x0 dx. Отказ в этом случае может произойти при условии, что прочность объекта будет меньше,
чем x0. Вероятность того, что прочность xп не превышает некоторое значение нагрузки x0 равна
|
x0 |
|
P xп x0 fп x dx. |
|
|
|
0 |
|
Нагрузка и прочность - случайные величины |
|
|
fH(x) |
fH(x) |
|
fП(x) |
|
|
|
fП(x) |
|
Н |
П |
x |
а) общий вид модели |
|
|
15
fH(x) |
fH(x) |
fП(x) |
fП(x) |
fH(x0) |
|
fП(x0) |
|
x0 |
x |
dx |
|
б) увеличенный масштаб области перекрытия |
|
Рис. 1.1
Но нагрузка xн может меняться в интервале (0, ). Поэтому для определения вероятности отказа необходимо проинтегрировать полученное вы-
ражение на этом интервале, заменив x0 на x
Q |
|
x |
|
(1.9) |
fн |
(x) |
(y)dy dx. |
||
|
fп |
|
|
|
|
|
0 |
|
|
Справедливо и другое уравнение
Q |
|
|
|
(1.10) |
fп |
(x) |
(y) dy dx. |
||
|
fн |
|
|
|
|
0 |
x |
|
|
Такие уравнения не имеют показателя наработки, поэтому модель отказа "нагрузка - прочность случайные величины" дает возможность рассчитать вероятность отказа или безотказной работы, но не позволяет определить функцию надежности и другие показатели, связанные с наработкой.
Не всегда удается проинтегрировать уравнения для вероятности отказа в элементарных функциях. В общем случае может потребоваться численное интегрирование. Ниже приводится ряд формул для нахождения вероятности отказа при различных законах распределения случайных величин нагрузки и прочности. Математические выкладки опущены.
16

Прочность и нагрузка имеют распределение Гаусса (нормальное)
|
|
1 |
|
|
z |
2 |
|
|
|
Q 1 |
|
|
|
exp( |
|
|
)dz, |
(1.11) |
|
|
|
|
2 |
||||||
2 |
|||||||||
|
|
|
a |
|
|
||||
|
|
|
|
|
|
|
|
||
где a = |
п |
н |
|
; |
|
|
|
|
|
||
|
|
п2 |
н2 |
||
п и н - соответственно параметры центра распределения (математические ожидания) случайной величины прочности и нагрузки;
п и н - соответственно параметры рассеяния (средние квадратические отклонения) прочности и нагрузки.
Вероятность отказа можно выразить через нормальное распределение нормированной случайной величины.
|
|
|
|
|
|
|
|
|
|
|
|
|
п н |
|
|
|
|
|
|
|
|
|
|
|
|
Q Фн |
|
|
|
|
, |
(1.12) |
|||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
п2 н2 |
|
|
||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
||||
где |
Фн(x) |
|
|
|
|
exp( |
|
z |
|
)dz . |
|
|
|
|
|
(1.13) |
||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Прочность и нагрузка имеют экспоненциальное распределение
Q 1 |
н |
, |
(1.14) |
|
п н
где н и п - соответственно параметры распределений нагрузки и прочности.
Прочность имеет распределение Гаусса, а нагрузка - экспоненциальное
|
|
|
|
п |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
2) |
|
||
Q |
|
|
|
|
exp |
|
(2 |
п |
|
|
н |
|
|
|
||||||||||
|
|
|
|
|
||||||||||||||||||||
|
Фн |
|
п |
|
|
|
|
2 |
|
|
|
|
|
н |
|
п |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.15) |
|||||
|
|
|
|
|
|
|
|
|
п |
|
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
н п |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 Фн |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
17
где п и п - соответственно параметр центра (математическое ожидание) и параметр масштаба (среднее квадратическое отклонение) прочности;
п - параметр распределения нагрузки.
Фн(x) - здесь и далее определяется по формуле (1.13).
Прочность и нагрузка имеют гамма - распределение
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
Г( |
п |
|
н |
) |
|
(1 r) |
|
|
1 |
|
|
|
1 |
|
|
Q 1 |
|
|
|
|
|
1-U |
п |
|
U |
|
н |
|
dU, |
(1.16) |
||
|
|
|
|
|
|
|
|
|||||||||
|
Г( п) Г( н) |
0 |
|
|
|
|
|
|
|
|
|
|||||
где Г(x) - гамма функция, см. прил. 2;
п и н - соответственно параметры формы распределения прочности и нагрузки;
r н п ;
п ;
п, н - соответственно параметры масштаба распределения прочности и нагрузки.
Нагрузка имеет распределение Гаусса, прочность - Вейбулла
|
|
|
|
|
|
|
|
x |
0п н |
|
|
|
|
|
1 |
|
|
п x0п |
|
|
|
|||||||
|
|
Q 1 Ф |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
н |
|
н |
|
|
|
|
|
|
2 |
|
|
|
|
н |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.17) |
||||||
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
2 |
|||||
|
|
|
|
|
|
|
0п |
|
|
|
0п |
н |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
exp |
|
y |
|
п |
|
|
|
|
п |
|
|
y |
|
|
|
|
dy, |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где x0п, п, п - соответственно параметры сдвига, формы и масштаба распределения прочности;
н, н - соответственно параметры центра и масштаба распределения нагрузки.
Прочность и нагрузка имеют распределение Вейбулла
|
|
|
|
п |
1 |
|
x0п x0н |
|
н |
|
||
|
|
|
|
|
|
|
|
|||||
Q |
|
exp( y) exp |
|
|
y |
п ( |
|
) |
|
dy, |
(1.18) |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
н |
|
|
н |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
18
где x0п, п, п - соответственно параметры сдвига, формы масштаба распределения прочности;
x0н, н, н - соответственно параметры центра и масштаба распределения нагрузки.
Рассмотрим влияние параметров и взаимного расположения кривых плотностей распределения нагрузки и прочности на вероятность отказа. Отношение математических ожиданий прочности и нагрузки принято называть коэффициентом запаса.
KЗ‚ |
|
п |
. |
(1.19) |
|
|
|||||
|
|
|
н |
|
|
|
|
|
|
||
Покажем, как влияют на вероятность отказа изменения математических ожиданий и коэффициентов вариации (см. прил. 2) распределений. Для простоты будем считать параметры распределения нагрузки неизменными.
Пусть имеются некоторые плотности распределений нагрузки fн(x) и прочно-
сти fп(x), показанные на рис. 1.2, а). При уменьшении математического ожидания прочности (Рис. 1.2, б) площадь перекрытия возрастает, а следовательно, возрастает и вероятность отказа. Фактически это означает, что снижение коэффициента запаса приводит к росту вероятности отказа. Теперь допустим, что прочность имеет такое же математическое ожидание, как на рис. 1.2, а), но коэффициент вариации выше. Эта ситуация показана на рис. 1.2, в). Коэффициент запаса прочности не изменился, но вероятность отказа возросла. Это произошло из-за того, что больший коэффициент вариации привел к большему перекрытию распределений. Указанные эффекты наглядно иллюстрирует рис 1.2, г), где показана зависимость вероятности отказа от коэффициента запаса при различных коэффициентах вариации, для случая, когда нагрузка и прочность имеют распределение Гаусса. Из рис. 1.2 можно сделать важный для практики вывод о значении высоких технологий. Высокие технологии позволяют изготовлять объекты с большой степенью точности, и, следовательно, с низким значением коэффициента вариации прочности. Это позволяет значительно снизить коэффициент запаса не увеличивая вероятность отказов и не снижая надежности объектов. Снижение коэффициентов запаса, в свою очередь, позволяет снижать массу, габариты и стоимость объектов.
19

Влияние параметров распределений на вероятность отказа в модели: нагрузка и прочность - случайные величины
fн(x) |
|
Кза |
fн(x) |
|
f (x) |
|
на |
f |
(x) |
п |
|
па |
п |
|
|
|
|
|
|
|
|
Qа |
|
|
н |
п |
x |
|
|
|
а) |
|
|
|
fн(x) |
|
Кзв = Кза |
|
|
fп(x) |
|
нв = на |
|
|
|
|
пв > па |
|
|
|
|
Qв > Qа |
|
|
н п x
в)
|
|
|
|
Кзб < Кза |
|
|
|
|
нб = на |
|
|
|
|
пб = па |
|
|
|
|
Qб > Qа |
|
н |
п |
|
x |
|
|
б) |
|
|
Q |
|
|
|
|
0,4 |
|
|
νП=νН |
|
0,3 |
|
|
||
0,2 |
|
|
|
νП=0,5 |
0,1 |
ν =0,01 |
|
νП=0,3 |
|
|
П |
|
|
|
|
1,2 1,4 |
1,6 |
1,8 |
2,0 КЗ |
|
|
г) |
|
|
Рис. 1.2
Лекция №4
4. МОДЕЛЬ ОТКАЗА: НАГРУЗКА И ПРОЧНОСТЬ - СЛУЧАЙНЫЕ ПРОЦЕССЫ
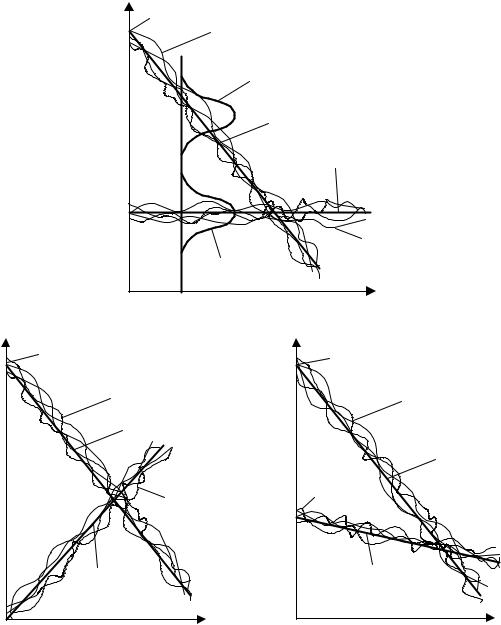
В реальных условиях нагрузка и прочность часто могут изменяться со временем. В этом случае можно говорить о случайных процессах ([1], прил. 4) изменения нагрузки и прочности. На рис. 1.3 показаны три характерных ситуации. Прочность и нагрузку будем считать случайными процес-
сами xп(t) и xн(t). Под действием нагрузки xн(t) прочность непрерывно уменьшается до тех пор, пока объект не выйдет из строя. Время безотказной работы объекта определяется функцией распределения Q(t). Функция Q(t) зависит от значений прочности и нагрузки, значений параметров их законов
распределений, а также от взаимосвязи функций xп(t) и xн(t).
20
Для получения аналитических зависимостей вероятности отказа объекта Q(t) и других показателей надежности выразим нестационарные случай-
ные функции xп(t) и xн(t) через более простые типы случайных функций. Для модели на рис. 1.3, а) нагрузка - стационарный случайный процесс с параметрами
Xн t Xн,
Xн t Xн.
Прочность - нестационарный случайный процесс с монотонно убывающим математическим ожиданием
xп t xп t , |
(1.20) |
где xп(t) - случайная величина;
п(t) - неслучайная функция усталости. Тогда п(t) = п(0) (t). Модель (вид) функции (t) зависит от характера физико-химических
процессов, протекающих в объекте под действием нагрузок. Например, это может быть экспоненциальная функция вида
t exp kt . |
(1.21) |
Свойства функции усталости:
t 0 1;
lim t 0. t
Модель отказа: нагрузка и прочность - случайные процессы
21
|
Xн(t) |
п(0) |
Xп(t) |
|
|
Xп(t) |
|
|
|
|
|
|
fп(x, t1) |
|
|
|
|
п(t) |
|
|
|
|
|
н(t) |
|
|
|
|
Xн(t) |
|
|
|
fн(x, t1) |
|
|
|
t1 |
а) |
t |
Xн(t) |
п(0) |
|
Xн(t) |
п(0) |
Xп(t) |
Xп(t) |
Xп(t) |
Xн(t) |
|
|
|
|
|
|
|
|
п(t) |
|
п(t) |
|
|
|
|
|
|
|
Xн(t) |
|
Xп(t) |
|
н(t) |
|
|
(t) |
|
|
|
|
н |
|
б) |
|
t |
t |
|
|
|
в) |
|
а) нагрузка - стационарный процесс: прочность - нестационарный процесс; |
||||
б) нестационарная возрастающая нагрузка; |
|
|||
в) нестационарная убывающая нагрузка. |
|
|||
Рис. 1.3
При независимых нагрузках и прочности, выражение для вероятности отказа имеет вид
22
