2. Абсолютно неупругий удар

Пусть абсолютно не упруго сталкиваются два тела с массами m₁иm₂, движущихся со скоростямии. Считаем, что тела образуют замкнутую систему. По закону сохранения импульса

.

Отсюда скорость после столкновения равна

.

Из этой формулы видно, что после столкновения тела двигаются вдоль диагонали параллелограмма, построенного на векторах и.

Закон сохранения суммарной энергии в случае абсолютно неупругого удара запишется в виде

+ А_деформ.

4.5. Задание для самоконтроля знаний

_{1. Определить скорость вагонов одинаковой массы после неупругого столкновения, если они двигались навстречу со скоростями и} .

2. На сколько изменится угловая скорость фигуриста при его вращении, если он изменит свой момент инерции в 2 раза.

_{3. Определить потенциальную, кинетическую и полную энергию тела массой 1кг падающего с высоты 2м на середине пути и в точке удара о Землю.}

_{4. Определить скорость второго шара u2 после упругого столкновения его с первым шаром, движущимся со скоростью υ1 = 10 м/с, если их массы равны, а до столкновения скорость второго шара υ2 = 0 м/с.}

_{5. Определить скорость двух вагонов массой 10т, движущихся вместе после их не упругого столкновения, когда один стоял, а другой двигался со скоростью 20 км/час.}

Глава 5. Механические волны

Лекция 7

5.1 Продольные и поперечные волны

Если какую-либо частицу или совокупность частиц упругой среды привести в колебательное движение, то колебания не останутся локализованными в том месте, где они возникли, а благодаря взаимодействию между частицами будут распространяться с некоторой скоростью по всем направлениям. Процесс распространения механических колебаний в упругой среде называется механической волной.

В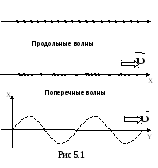волне частицы среды лишь совершают колебания около положений равновесия, причем соседние частицы, даже самые ближайшие, колеблются с некоторым сдвигом по фазе. Наличие сдвига фаз объясняется упругим взаимодействием между частицами которое распространяется в среде с конечной скоростью.

Различают поперечные и продольные волны. Волна называется поперечной, если колебания частиц среды происходят вдоль направлений, перпендикулярных к направлению распространения волны (например, колебания струны). Поперечные волны могут распространяться в тех средах, в которых возникают упругие силы при деформации сдвига.

Волна называется продольной, если колебания частиц среды происходят вдоль направлений, параллельных направлению распространения волны (например, звуковые волны). Продольные волны распространяются в упругих средах при их сжатии или растяжении

Расположение частиц в упругой среде в момент возникновения продольной или поперечной волны приведены на рис. 5.1. До появления волны частицы среды вдоль направления хнаходились на одинаковых расстояниях.

Распространение волны в упругой среде происходит с фазовой скоростью , частотой колебаний, периодом колебаний Т, циклической частотойи длиной.

Фазовая скорость, или скорость распространения волны , - это скорость с которой перемещается в пространстве фаза колебания. Фазовая скорость зависит от плотности среды и ее упругих свойств.

Частота колебаний - число полных колебаний частиц среды за единицу времени.

Период колебаний Т – промежуток времени, в течение которого частицы совершает одно полное колебание.

Циклическая частота - число полных колебаний, совершаемых за 2секунд.

Длина волны– расстояние между ближайшими частицами, с одинаковой фазой или сдвигом фаз равным 2.

Волновая поверхность – это геометрическое место точек, колеблющихся в одинаковой фазе. Волновые поверхности проводятся через равновесные положения частиц, колеблющихся в одинаковых фазах и поэтому они неподвижны. В зависимости от формы волновой поверхности различают плоские, сферические, цилиндрические, эллиптические волны и др.

Поверхность, отделяющая колеблющиеся частицы от частиц, находящихся в покое называется фронтом волны. Фронт волны в отличие от волновых поверхностей перемещается со скоростью, равной скорости распространения волны.

Нормаль восстановленная в точке фронта волны определят направление распространения волны.

Параметры волны связаны между собой соотношениями

(5.1)

Отношение называется волновым числом.