tezisu

УДК 517.983:519.642

СРАВНЕНИЕ ДВУХ АЛГОРИТМОВ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ ДВУМЕРНОЙ 2-ТЕНЗОРНОЙ ТОМОГРАФИИ

Светов Иван Евгеньевич Институт математики им. С.Л.Соболева СО РАН, г. Новосибирск, Россия

Новосибирский государственный университет, г. Новосибирск, Россия

заполненном средой с прямолинейным характером распространения лучей. По известным значениям продольного, и (или) смешанного, и (или) поперечного лучевых преобразований требуется восстановить 2-тензорное поле u .

преобразованию можно восстановить лишь соленоидальную часть d 2 , в то время как, по смешанному и поперечному лучевым преобразованиям

соответственно.

В данном докладе для построения аппроксимации соленоидальной и (или) потенциальной части искомого симметричного 2-тензорного поля использовались два алгоритма: 1) алгоритм, основанный на методе наименьших квадратов, а в качестве аппроксимирующей последовательности выступают соленоидальные и потенциальные симметричные 2-тензорные поля, построенные на основе двумерных B- сплайнов [1]; 2) алгоритм, основанный на методе сингулярного разложения операторов лучевых преобразований симметричных 2-тензорных полей [2].

Работа проводилась при поддержке РФФИ (проект 14-01-31491- мол_а).

Литература

[1]Светов И.Е., Полякова А.П. Восстановление 2-тензорных полей, заданных в единичном круге, по их лучевым преобразованиям на основе МНК с использованием B-сплайнов. // Сибирский Журнал Вычислительной математики. - 2010. - Т. 13, №2. - С. 183-199.

[2]Деревцов Е.Ю., Полякова А.П. Решение задачи интегральной геометрии 2-тензорных полей методом сингулярного разложения. // Вестник Новосибирского государственного университета. Серия: математика, механика, информатика. - 2012. - Т.12, No. 3. - С. 73-94.

УДК 519.217.2

311

МАРКОВСКАЯ МОДЕЛЬ ЗАБОЛЕВАЕМОСТИ САХАРНЫМ ДИАБЕТОМ

Валитов Д.И.

Башкирский государственный университет, г. Уфа, Россия

Многие операции, которые приходилось анализировать под углом зрения выбора оптимального решения, развиваются как случайные процессы, ход и исход которых зависит от ряда случайных факторов, сопровождающих эти операции. Для того чтобы вычислить числовые параметры, характеризующие эффективность таких операций, нужно построить некоторую вероятностную модель явления, учитывающую сопровождающие его случайные факторы. В марковском случайном процессе будущее развитие его зависит только от настоящего состояния и не зависит от «предыстории» процесса. При математическом моделировании на основе марковских процессов возникают две взаимно противоположные задачи. Прямая, задача состоит в расчете вероятностей соответствующих состояний и другие характеристики процесса. Параметры модели при этом предполагаются известными. Обратная задача состоит в определении параметров модели на основе известных из эксперимента результирующих характеристик процессов. При рассмотрении процесса заболевания сахарным диабетом имеем размеченный граф с 4 состояниями – 1)здоров 2)болен, инсулинонезависим 3) болен, инсулинзависим 4) мертв.

В марковской модели исходные параметры - это интенсивности, или силы, перехода из состояния в состояние.

Поставленные в работе задачи решены с использованием теории марковских процессов, теории графов, метода Рунге-Кутта для решения системы дифференциальных уравнений.

При анализе использовались реальных данных по заболеваемости сахарным диабетом, предоставленные Медицинским информационно – аналитическим центром (МИАЦ) при Министерстве Здравоохранения Республики Башкорстостан.

Литература

1.Кошкин Г.М. Основы актуарной математики. – Томск: Томский Государственный университет, 2002. – 116 с.

2.Свешников А.А. Прикладные методы теории марковских процессов. Уч.пособие. – М.: Лань, 2007. – 192

3.В.Н. Костин, Н.А. Тишина. Статистические методы и модели. - Оренбург: ГОУ ОГУ, 2004. -138 с.

312

УДК 538.7

ВЫЧИСЛЕНИЕ МАКСИМАЛЬНОЙ ТОЧКИ ПОВОРОТА С ПОМОЩЬЮ ВАРИАЦИОННОГО ПОДХОДА

Иванов А.А.

Башкирский государственный университет, г. Уфа, Россия

Рассматривается новая парадигма нахождения бифуркаций решений нелинейных задач, которая основана на обнаружении экстремальных значений вариационных функционалов нового типа, связанных с рассматриваемыми задачами. Вариационные функционалы получают конструктивно методом продолженного функционала, который может быть применен к широкому классу параметрических задач, включая нелинейные дифференциальные уравнения с частными производными. Главной особенностью данного подхода является то, что он позволяет рассматривать задачу нахождения бифуркаций с новой геометрической точки зрения, а именно с помощью метода продолженного функционала. С помощью этого подхода доказаны необходимые и достаточные условия, которые обеспечивают существование бифуркаций типа максимальной точки поворота. На их основе вводится алгоритм квазинаправления наискорейшего подъема. Для иллюстрации поведения метода и обсуждения его преимуществ и недостатков по сравнению с альтернативными методами проведены численные эксперименты.

Литература

1.Иванов А.А., Ильясов Я.Ш., Нахождение бифуркаций для решений

нелинейных уравнений методами квадратичного программирования // Ж. вычисл. матем. и матем. физ. 2013. Т. 53, №3, с. 350–364.

Иванов А.А., 2014 г.

313

СЕКЦИЯ «ГРУППОВОЙ АНАЛИЗ»

УДК 517.925.4

СИММЕТРИИ СКАЛЯРНОГО ОДУ ВТОРОГО ПОРЯДКА И ДВУМЕРНЫХ УРАВНЕНИЙ ГЕОДЕЗИЧЕСКИХ

Багдерина Ю.Ю.

Институт математики с вычислительным центром УНЦ РАН, Уфа, Россия

Геодезические двумерной поверхности с римановой метрикой

описываются уравнениями

(1)

Любой системе (1) может быть поставлено в соответствие скалярное ОДУ второго порядка

(2)

относительно y(x). Обратное неверно, т.е. не всякое уравнение

(3)

представимо в виде (2), где 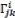− символы Кристоффеля некоторой невырожденной метрики. Например, уравнения Пенлеве, за исключением специальных случаев, такого представления не имеют. В данной работе получено необходимое условие представимости уравнения (3) в форме (2). Сопоставляются свойства симметрии уравнения (2) и системы (1). Показано, что уравнения (3), не имеющие представления (2), могут иметь симметрии.

314

УДК 512.54

ЭВАРИСТ ГАЛУА И ГРУППА ПОДСТАНОВОК

Макаримова Э.М.

Уфимский государственный авиационный технический университет, г. Уфа, Россия

До Галуа почти триста лет никому не удавалось решить общее уравнение пятой степени или выше. Он первым нашѐл те критерии, которые позволяли определить, существует ли решение данного уравнения в радикалах. Изложим результаты Галуа в современных терминах теории групп [1].

Каждое уравнение степени n можно связать с группой подстановок S(n) или какой-либо еѐ подгруппой. Такая группа отражает свойства симметрии уравнения и называется группой Галуа. Уравнение разрешимо в радикалах, только если его группа Галуа разрешима, то есть порождает последовательность вложенных нормальных подгрупп, для которых индексы (отношение порядка. основной группы к порядку еѐ подгруппы) будут являться простыми числами. Индексы, порожденные группой S(3) и двумя максимальными нормальными подгруппами, есть простые числа 2 и 3. Значит, и все уравнения третьей степени разрешимы. Можно доказать, что максимальная нормальная подгруппа группы A(n) есть единичная группа (I), состоящая только из нейтрального элемента. Поскольку A(n) — максимальная нормальная подгруппа группы S(n), не все индексы при n≥5 являются простыми числами. В частности, при n=5 индексы равны 2 и 60 [2]. Так что соответствующие уравнения неразрешимы в радикалах.

Вдохновленный идеями Галуа, норвежец Мариус Софус Ли вскоре обратился к решениям дифференциальных уравнений. Его исследования положили начало групповому анализу. Нахождение группы преобразований является способом проверки интегрируемости и получения семейства решений уравнения. Группу Галуа также можно трактовать как группу преобразований.[3]

Литература

1.Александров П.С. Введение в теорию групп. – М.:Наука, 1980. –

145 с.

2.Ротман, Тони. Короткая жизнь Эвариста Галуа // В мире науки., 1983, № 1, с. 84–93.

3.Ибрагимов Н.Х. Азбука группового анализа. – М.:Знание, 1989. –

48 с.

315

СЕКЦИЯ «МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЭКОНОМИКЕ»

УДК 51-77

МОДЕЛИРОВАНИЕ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ КОМПЛЕКСНОЗНАЧНЫМИ МОДЕЛЯМИ

Бекмурзина Г.Р., Смирнова Е.А.

Научный руководитель: доцент, к.ф.-м.н., Беляева М.Б.

СФ Башкирского государственного университета, г. Серлитамак, Россия Модели комплекснозначной экономики позволяют описать процессы, моделирование которых с помощью действительных переменных затруднено. [1] Важным преимуществом комплекснозначной является то, что моделируется зависимость сразу двух экономических показателей от других переменных. Наибольшую популярность описания таких зависимостей получили производственные функции, моделирующие зависимость производственного результата от производственных ресурсов при целом ряде исходных допущений. Для того чтобы произвести экономический анализ промышленности России, была построена степенная производственная функция комплексных переменных с действительными коэффициентами. Построенная модель имеет вид G iC 1.993(K iL)5.069 , где

G – месячная прибыль, C – затраты, K – стоимость ОПФ, L – средняя месячная заработная плата Оценки составляющих коэффициентов найдены

спомощью МНК по основе статистики за 2007-2013гг. Также были найдены переломные точки данной модели, и рассчитан уровень эффективности производственного процесса России. Расчѐт коэффициентов показал, что эффективность работы предприятий с каждым годом увеличивается, производство промышленности близко к оптимальному. При данной технологии производства предприятия могли бы получать большую прибыль и нести меньшие затраты. Полученная модель может быть использована руководителями предприятий для многовариантных расчѐтов

сцелью оптимизации производства. Таким образом, модель степенной производственной функции комплексных переменных показывает практическую применимость еѐ на макроуровне.

Литература

1. Светуньков И.С. Степенные производственные функции комплексных переменных//Экономика и математические методы. –2012г. – Т. 48. - №1. – С. 67-79.

316

УДК 519.865.5

МОДЕЛИ ФОРМИРОВАНИЯ ОПТИМАЛЬНОГО ПОРТФЕЛЯ ЦЕННЫХ БУМАГ

Буцык О.А.

Башкирский государственный университет, г. Стерлитамак, Россия

Развитие рыночной экономики и закрепление частной собственности в различных ее формах привело к тому, что наряду с денежными средствами широкое распространение в качестве средства платежа и инвестирования получили ценные бумаги. Необходимо учитывать, что вложения в ценные бумаги всегда сопряжены с определенным риском [1]. Рассмотрим несколько моделей формирования оптимального портфеля ценных бумаг.

Модель эффективного портфеля Г. Марковица (1952 г.)

Суть метода состоит в том, что инвестор в настоящий момент времени имеет конкретную сумму денег для инвестирования. В конце периода владения инвестор продает ценные бумаги, которые были куплены в начале периода, после чего либо использует полученный доход на потребление, либо реинвестирует доход в различные ценные бумаги) [1].

Модель Дж. Тобина (1950-1960 гг.)

Дж. Тобин преобразовал модель Г. Марковица за счет введения в портфель безрискового актива и возможности заимствования. Инвестор имеет возможность привлекать дополнительные заемные средства для увеличения своих вложений в портфель, составленный из рисковых, имеющих более высокую доходность, активов.

Модель оценки капитальных активов (У. Шарп (США) 1964 г., Дж. Линтер (США) 1965г.)

Модель оценки капитальных активов (capital asset pricing model, САРМ) была разработана с целью нахождения ответа на вопрос о том, какими должны были бы быть премии за риск, на которые согласны инвесторы в ситуации рыночного равновесия. [3].

Модель теории арбитражного ценообразования (С. Росс)

Главным предположением теории является то, что каждый инвестор стремится использовать возможность увеличения доходности своего портфеля без увеличения риска. Механизмом, способствующим реализации данной возможности, является арбитражный портфель.

Литература

1. Батяева Т.А., Столяров И.И. Рынок ценных бумаг: Учеб. пособие. – М.: ИНФРА-М, 2007. – 304 с.

2.Шарп У., Александер Г., Бэйли Дж. — ИНВЕСТИЦИИ: Пер.

сангл. — М.: ИНФРА-М, 2001. – 45 с.

317

УДК 330.142.211

ПРОБЛЕМЫ ИССЛЕДОВАНИЯ ДИНАМИКИ И МОДЕЛИРОВАНИЯ ОСНОВНЫХ ФОНДОВ

Хамитов Ильдар Шамилевич Башкирский государственный университет, г.Уфа, Россия

Измерение запасов и динамики основных фондов представляет собой серьезную проблему. В странах с переходной экономикой эти проблемы усугубляются изменением соотношением цен на инвестиционные товары и загрузки основных фондов, изменением спроса и конъюнктуры и другими трансформационными процессами [1]. Кроме того стоит отметить, что в России существует еще проблема перехода ведения статистики с номенклатуры ОКОНХ (Общесоюзного классификатора отраслей народного хозяйства) в 2005 г. к системе ОКВЭД (Общероссийского классификатора видов экономической деятельности). В результате была потеряна преемственность данных, что добавляет проблем в межотраслевой оценке основных фондов [2]. Изношенность основных фондов требует концентрация внимания государственных органов управления на проблемах воспроизводства основных фондов и на разработке комплекса мер [3]. Для решения данных задач, в которых необходим учет основных фондов можно выделить четыре подхода:1. Определение восстановительной стоимости основных фондов по результатам переоценок. Данный способ реализован в официальной статистике. 2. Оценка основных фондов на данных о загрузке мощностей промышленных предприятий 3. Определение динамики основных фондов через валовые инвестиции. 4. Подход основан на предпосылке о постоянстве срока службы основных фондов [1].

Последний подход позволяет учитывать искажения от переоценок и выявить динамику эффективных основных фондов. Реализовать данных подход можно на основе производственной функции Кобба-Дугласа, где в свою очередь основные фонды определяются как функция дожития.

Литература

[1]Воскобойников И.Б. О корректировке динамики основных фондов// Экономический журнал ВШЭ. 2004. Т. 8. № 1.– С.3-20.

[2]Ким И.А. Построение систем таблиц «Затраты – Выпуск» России для 1995–2003 гг. в «смешанной» номенклатуре ОКОНХ–ОКВЭД // Экономический журнал ВШЭ. 2011. Т. 15. № 3.– С.336–352

[3]Ахунов Р.Р., Юсупов К.Н., Янгиров А.В. О проблемах воспроизводства основных фондов в Республике Башкортостан//Экономика

иуправление: научно-практический журнал. 2013. № 6.– С.32-36.

318

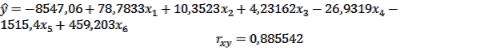
УДК 330.4

АНАЛИЗ ВРЕМЕННЫХ СВЯЗЕЙ И КОРРЕЛЯЦИЙ БИРЖЕВЫХ ИНДЕКСОВ МЕЖДУНАРОДНЫХ КОМПАНИЙ

Мухамадиева Алина Ильгизаровна Стерлитамакский филиал Башкирского Государственного Университета,

г.Стерлитамак, Россия

Функционирование и успешное развитие рынка ценных бумаг невозможно без наличия информации о биржевых процессах. В странах с развитой экономикой придается первостепенное значение анализу биржевой конъюнктуры, тенденций и деловой активности фондового рынка. Необходима постоянная оперативная информация о рыночной ситуации, о состоянии и изменении курсов акций и т.д. Эти экономические процессы разворачиваются во времени и их можно представить системой количественных и качественных показателей, зависящих от времени. В этой связи, при прогнозировании экономических явлений особое внимание уделяется изучению временных рядов. Пусть имеются биржевые индексы компаний «Лукойл», «Nikkei», «American Express Company», «DAX», «FTSE», «CAC-40» и «TOPIX» за последние 12 месяцев, согласно данным сайта moex.com. Проведем анализ данных индексов и построим регрессионную модель. Обозначим за y биржевые индексы компании

«Лукойл», 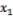– компании «Nikkei», 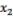– «American Express Company», –

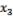«DAX», 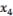– «FTSE», 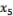– «CAC-40», 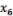– «TOPIX». Используя инструмент анализа данных Excel «Регрессия» найдем уравнение регрессии и коэффициент корреляции. Получим уравнение регрессии:

детерминации 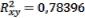говорит о хорошей взаимосвязи между результативным признаком и исследуемыми факторами, то есть уравнением регрессии объясняется 78,39% дисперсии результативного признака, а на долю прочих факторов около 22% ее дисперсии, и значит, модель регрессии хорошо аппроксимирует исходные данные.

Литература

1. Федосеев В.В и др. Экономико-математические методы и прикладные модели: Учеб.пособие для вузов/Под ред.В.В.Федосеева.-

М.:ЮНИТИ, 1999.- 391 с.

319

УДК 51-77

РЕШЕНИЕ ЗАДАЧ НЕЧЕТКОЙ ЛОГИКИ С ПОМОЩЬЮ ПАКЕТА

FUZZY LOGIC TOOLBOX MATLAB

Малышева К.А., Научный руководитель: доцент, к.ф.-м.н., Беляева М.Б СФ Башкирского государственного университета, г.Стерлитамак, Россия

В последнее время одной из наиболее активных и перспективных направлений прикладных исследований в области управления и принятия решений является нечеткое моделирование. Нечеткая логика более естественно описывает характер человеческого мышления и ход его рассуждений. Именно поэтому изучение и использование математических средств, представляющих нечеткую исходную информацию, позволяет строить модели, наиболее адекватно отражающие неопределенность окружающей нас реальности. [1]. В качестве иллюстрации практического применения Fuzzy Logic системы MATLAB была рассмотрена задача оценки финансовой состоятельности клиентов банка при выдаче долгосрочных кредитов на строительство зданий под залог. При этом в качестве нечеткой модели использована схема нечеткого вывода с входными и выходными переменными. Используя метод экспертных оценок, для оценки финансовой состоятельности клиентов были выбраны следующие характеристики: месторасположение строящегося здания, качество предполагаемого выполнения отделочных работ, оценка активов потенциального клиента, оценка дохода потенциального клиента за вычетом фиксированных расходов, величина подлежащих уплате процентов по кредиту. При этом финансовая состоятельность клиента оценивается его кредитоспособностью. Все рассматриваемые переменные измеряются в баллах в интервале действительных чисел от 0 до 10. В качестве схемы нечеткого вывода использован метод Мамдани.

После выполнения анализа построенной системы нечеткого вывода и разработки нечеткой модели, были введены данные экспертных оценок для входных переменных и получено значение выходной переменной.

Таким образом, разработка нечетких моделей позволяет адекватно оценивать и решать задачи в условиях неопределенности реального мира и мышления человека, дает возможность получения приемлемого решения.

Литература

1.Леоленков А.В. Нечеткое моделирование в среде MATLAB и fuzzyTECH. – СПб., 2003. – С.736.

2.Fuzzy Logic Toolbox. User‘s Guide, The MathWorks, Inc., 2014.

Малышева К.А., 2014 г.

320