tezisu

УДК 517.9

О РАЗЛОЖЕНИИ ФИШЕРА ДЛЯ ОПЕРАТОРОВ С ОДНОРОДНЫМИ ХАРАКТЕРИСТИЧЕСКИМИ ФУНКЦИЯМИ

Губайдуллина Эльвира Фанировна Институт математики с ВЦ УНЦ РАН, г. Уфа, Россия

Разложение Фишера - это представление заданного пространства функций в виде ядра дифференциального оператора и главного идеала. Характеристическая функция дифференциального оператора и функция, порождающая идеал, называются парой Фишера. Изучение пар Фишера началось с работы Фишера [1] 1917г., в которой получена следующая

Нам было сообщено, что в данной работе была допущена ошибка. Нами был найден новый метод доказательства теоремы Шапиро, опирающийся на оценки коэффициентов разложения целой функции в ряд.

Литература

[1]Fisher E. // J.Math. 148 (1917), p. 1-78.

[2]Shapiro H.S. An algebraic theorem of E.Fisher, and the holomorphic Goursat problem // Bull. London Math. Soc. 21 (1989), p. 513-537.

261

30H10; 47A15

INVARIANT SUBSPACES OF THE HARDY SPACE OVER THE

POLYDISC

Koca B.B.

Department of Mathematics

Istanbul University, Istanbul, Turkey

In the fundemantal work [1], Beurling established that every invariant subspace of the Hardy space over the disc H 2 under the multiplication operator by the independent variable is generated by a single inner function. It is clear that in the case of the Hardy space over the polydisc H 2 2 , the subspaces generated by inner functions are also invariant under the multiplication

multiplication operators by the independent variables is generated by two functions and can not be generated by any one function. Moreover Rudin [3] gave

an example of invariant subspace of H 2 2 that are not finitely generated.

Further, he showed that there are invariant subspaces of H 2 2 that contain no

bounded elements in contrast with one variable case, every invariant subspaces contains and generated by a bounded function. Therefore ‗‘one can ask for a classification or an explicit description (in some sense) of all invariant subspaces

of H 2 2 ‘‘. This question was asked by Rudin in his book [3, p.78]. In this

talk we describe invariant subspaces of the Hardy space over the polydisc under the multiplication operators by the independent variables which are generated by an inner function. Then we show that existence of invariant subspaces of the Hardy space over the polydisc under the multiplication operators by the independent variables which are generated by a non-inner function.

References

1.A. Beurling, On two problems concerning linear transformations in Hilbert space, Acta Math. 81, (1948).

2.C.A. Jacewicz, A nonprincipal invariant subspace of the Hardy space on the torus, Proc. Amer. Math. Soc. 31, 127-129 (1972)

3.W. Rudin, Function theory in polydiscs, W. A. Benjamin, Inc., New YorkAmsterdam, 1969, p.vii+188

262

УДК 538.1

ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ВЫПУКЛЫХ ФУНКЦИЙ

Рахимова А.И.

Башкирский государственный университет, г. Уфа, Россия

Литература

1. Луценко В.И., Юлмухаметов Р.С. Обобщение теоремы Пэли – Винера на весовые пространства // Математические заметки. 1990. Т. 48, № 5. С.

80 – 87.

© Рахимова А.И., 2014 г.

263

УДК 517.81

ОБ ОДНОЙ ЗАДАЧЕ ОПЕРАТОРА СВЕРТКИ НА ВЫПУКЛЫХ ОБЛАСТЯХ

Зименс Карина Раисовна, Напалков Валентин Васильевич Уфимский государственный авиационный технический университет,

Литература

[1] Левин Б.Я. Распределение корней целых функций. М.: Гос. издат. техн.-теоретич. лит-ры. 1956. 632 с.

264

СЕКЦИЯ «ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ»

УДК 517.955.8

АСИМПТОТИКА ЭЛЕКТРИЧЕCКОГО СОПРОТИВЛЕНИЯ

Ершов А.А.1, Гадыльшин Р.Р.2 1Челябинский государственный университет, г. Челябинск, Россия,

2Башкирский педагогический университет им. М. Акмуллы, г. Уфа, Россия

Пусть x (x1, x2 , x3 ) , – ограниченная односвязная область в 3 с

границей С . И пусть эта область имеет два конечных плоских участка, с которыми мы свяжем две декартовые координатные системы

где n – внешняя нормаль. Методом согласования асимптотических разложений [1] построено асимптотическое разложение функции u(x,е) по

Получена следующая формула для электрического сопротивления образца

g1 и g2 – некоторые функции, зависящие только от x и .

Работа первого автора поддержана РФФИ (проект № 14-31-50424-мол_нр) и "Фондом поддержки молодых ученых "Конкурс Мѐбиуса". Работа второго автора выполнена в рамках базовой части государственного задания в сфере научной деятельности Минобрнауки России.

Литература

1. Ильин А. М. Согласование асимптотических разложений решений краевых задач. – М.: Наука, 1989. – 336 с.

265

УДК 517.929.7:517.929.8

ЗАДАЧА ДИРИХЛЕ ДЛЯ ОПЕРАТОРА ШРЕДИНГЕРА С БЫСТРООСЦИЛЛИРУЮЩИМ И ДЕЛЬТООБРАЗНЫМ ПОТЕНЦИАЛАМИ

Гадыльшин Т. Р.

Уфимский государственный авиационный технический университет, г. Уфа, Россия

В работе рассматривается следующая краевая задача:

Литература

1.Ильин А. М., Данилин А. Р. Асимптотические методы в анализе – М.: Физматлит, 2009.

2.Альбеверио С., Гестези Ф., Хѐэг-Крон Р., Хольден Х. Решаемые модели в квантовой механике – М.: Мир, 1991.

Гадыльшин Т.Р., 2014 г.

266

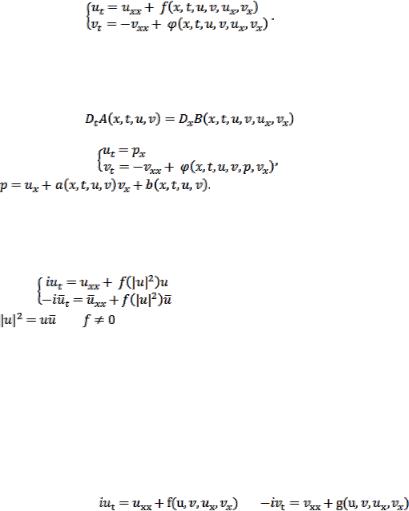
УДК 517.95

ЗАКОНЫ СОХРАНЕНИЯ НУЛЕВОГО И ПЕРВОГО ПОРЯДКОВ ДЛЯ ОДНОЙ ЭВОЛЮЦИОННОЙ СИСТЕМЫ УРАВНЕНИЙ.

Гайсина Регина Науфилевна Башкирский государственный университет, г. Уфа, Россия

В настоящей работе рассматривается система уравнений вида:

(1)

Определены системы уравнений (1),которые обладают законами сохранения нулевого и первого порядков.

Справедливо следующее утверждение.

Теорема. Система уравнений (1), которая имеет закон сохранения нулевого порядка

точечными преобразованиями приводится к системе вида:

(3)

где

Получены условия на правые части системы уравнений (3), при которых она обладает законом сохранения первого порядка:

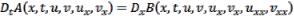. (4)

Также в работе рассмотрены частные случаи системы уравнений (1). Например, нелинейное уравнение Шредингера:

Законы сохранения нулевого и первого порядков имеют вид: 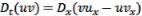и

.

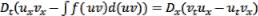Отметим, что в работах [1],[2] найдены классы уравнений типа (1), обладающие бесконечным набором законов сохранения.

Литература

[1] Михайлов А.В., Шабат А.Б. Условия интегрируемости систем двух

уравнений вида 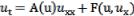.I //ТМФ. 1985. Т. 62, № 2. С. 163185.

[2] Шабат А.Б., Ямилов Р.И. О полном списке интегрируемых систем

ЗАДАЧА ДИРИХЛЕ ДЛЯ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ С ПЕРЕМЕННЫМ ПОКАЗАТЕЛЕМ НЕЛИНЕЙНОСТИ

Камалетдинов Александр Шамилевич (научный руководитель - Кожевникова Л.М.),

СФ БашГУ, г. Стерлитамак, Россия

Для анизотропного квазилинейного эллиптического уравнения второго

порядка в произвольной неограниченной области рассматривается задача Дирихле

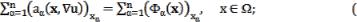1)

(2)

Предполагается, что функции 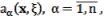каратеодоривы, пусть

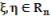справедливы неравенства

(3)

(4)

(5)

Здесь 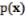измеримая и удовлетворяют условию

Теорема. Пусть выполнены условия (3) - (5), тогда существует единственное обобщенное решение задачи (1), (2)

268

УДК 159

ЧАСТНЫЕ РЕШЕНИЯ ОДНОГО УРАВНЕНИЯ В КОНЕЧНЫХ РАЗНОСТЯХ.

Хакимова Айгуль Ринатовна Башкирский государственный университет, г. Уфа, Россия

Данная работа посвящена методу обратной задачи рассеяния . К дискретной системе

были применены общие схемы построения явного частного решения. Заданная дискретная система является условием совместности пары

линейных уравнений вида: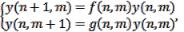

где 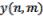матричная функция. Итак, имеется два уравнения на одну неизвестную функцию. В общем случае, такая система не имеет решений. В нашем случае система имеет решение, если она является условием

коммутирования двух дискретных операторов 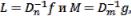где

- оператор сдвига по переменной , -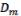

по 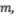иными словами выполняется следующее условие: 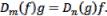Метод нахождения явного частного решения подробно описан в [1] и

применен к заданной динамической системе. В общем случае, решение

В некоторых случаях, 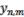можно записать компактно в удобной форме:

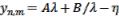, с помощью которой можно легко найти явные частные решения. В нашем случае решение имеет вид:

где м,з,p,q константы.

Литература

[1]И.Т. Хабибуллин, А.Г. Шагалов, Численная реализация метода обратной задачи рассеяния. Физика. Том 83, №3, июнь, 1990г.

[2]М. Абловиц, Х. Сегур, Солитоны и метод обратной задачи. М., 1987.

269

РАСПРЕДЕЛЕНИЕ ПОЛЮСОВ РЕШЕНИЙ УРАВНЕНИЯ ПЕНЛЕВЕ-4

Щелконогов Алексей Александрович Уфимский государственный авиационный технический университет,

г. Уфа, Россия

Работа посвящена изучению распределения полюсов специальных решений нелинейного уравнения Пенлеве-4. Эти решения представляют собой рациональные функции. Задача состоит в вычислении этого распределения в пределе при бесконечном числе полюсов. Впервые подобную задачу поставил и решил Т.Стилтьес в 1885 году на вещественной прямой, причем в его ответе координаты зарядов совпадали с нулями классических полиномов Эрмита.

В данной работе исследуется поведение полюсов решений уравнения Пенлеве-4 на комплексной плоскости в случае бесконечного числа полюсов. Методом скейлингового предела показано, что полюса решений уравнения Пенлеве-4 в предельном случае совпадают с нулями эллиптической функции Вейерштрасса, а также при определенных условиях с полюсами эллиптического синуса.

Литература

[1]И.Р. Итс, А.А. Капаев, В.Ю. Новокшенов, А.С. Фокас, «Трансценденты Пенлеве. Метод задачи Римана», Москва, Ижевск, 2005.

[2]Г. Бейтмен, А. Эрдейн. Высшие трансцендентные функции. Эллиптические и автоморфные функции. Функции Ламе и Матье, Москва, 1967, с. 9-68.

УДК 517.9

ФОРМАЛЬНАЯ ДИАГОНАЛИЗАЦИЯ ОПЕРАТОРА ЛАКСА И ЗАКОНЫ СОХРАНЕНИЯ ДИНАМИЧЕСКИХ СИСТЕМ1 Янгубаева Марина Валерьевна, УГУЭС, г.

Уфа, Россия

Исследуется динамическая система ε(DmDnu,Dmu,Dnu,u) = 0, пара Лакса

1 Работа выполнена при поддержке РФФИ: гранты № 13-01-00070 А, 14-01-97008 р_поволжье_а

270