4.1.3 Ітераційний метод Гауса - Зейделя

Даний метод виключно зручний для використання на ЕОМ, так як легко програмується, але не завжди дає послідовність значень невідомих, що наближаються до точного розв'язання системи (тобто не завжди сходиться). Проілюструємо його на прикладі системи з трьома невідомими. Якщо коефіцієнти ,, і, то систему (4.1) можна записати в наступному вигляді:

(4.19)

(4.20)

(4.21)

Задамося першим наближенням до вирішення цієї системи, позначивши його ,, (зазвичай вибирають). Підставивши цей розв’язок в (4.19), обчислимо нове значення:

(4.22)

Підставивши знайдене значення та значення в (5.20), обчислимо нове значення :

(4.23)

Аналогічно:

(4.24)

Цим закінчується перша ітерація. Замінивши значення ,,на,, відповідно, повторимо зазначений процес і отримаємо наступне наближення. У загальному випадку, для системи з рівнянь-е наближення до розв'язку системи буде обчислюватися по формулі:

(4.25)

де

Ітерації потрібно повторювати до тих пір, поки всі не стануть досить близькі до. Умова закінчення ітераційного процесу можна задати у вигляді:

, (4.26)

де - похибка розв’язання.

Ітераційний метод Гауса - Зейделя сходиться в тому випадку, якщо виконуються умови:

для всіх , і по крайній мірі ( 4.27 а)

для одного , (4.27 б)

де - модуль .

Іншими словами, кожний діагональний елемент матриці системи повинен бути більше суми елементів відповідної стрічки (по модулю). Наприклад, для системи:

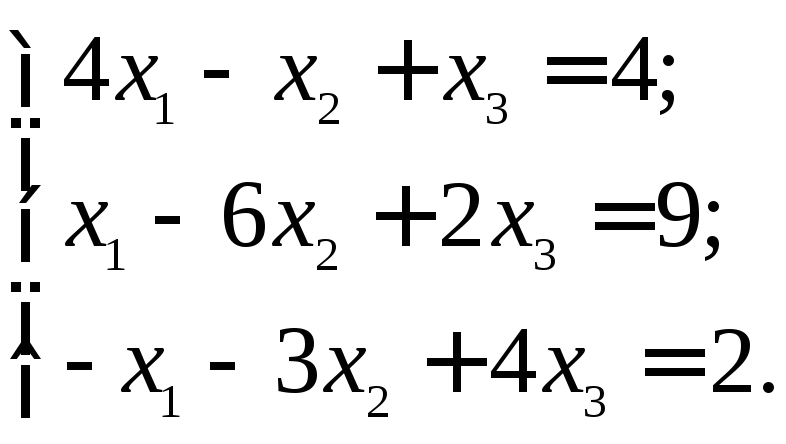
Для даної системи рівнянь метод Гауса-Зейделя є збіжним, оскільки виконуються умови (4.27):

.

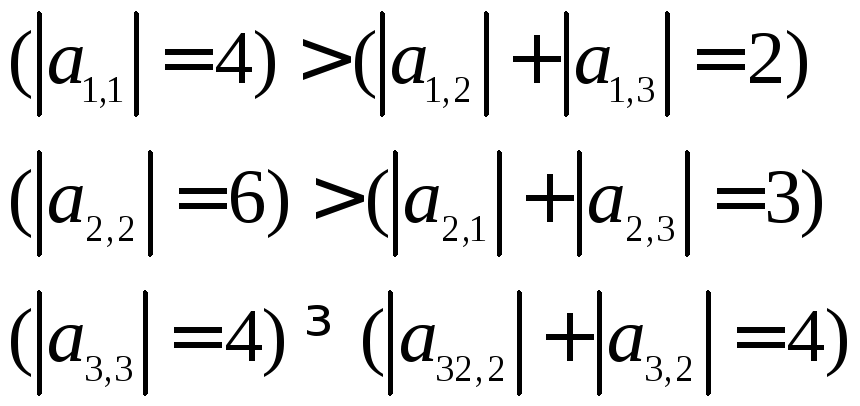Оскільки алгоритм методу Гауса–Зейделя нескладний, то його складові при виконанні лабораторної роботи виконуються самостійно.

5.2 Чисельні методи знаходження коренів поліномів

Як було показано в попередньому розділі, модель лінійної динамічної системи може бути представлена у вигляді передаточної функції у вигляді дробу, в якому чисельних і знаменник є поліномами оператора Лапласа s або оператора диференціювання p. Корені цих поліномів відіграють важливу роль у визначанні таких характеристик динамічних систем, як стійкість і точність, запас стійкості та інш. Нелінійни динамічні системи часто описуються математичними моделями у вигляді нелінійних і трансцендентних рівнянь. Тому важливо вміти використовувати комп’ютерні методи знаходження коренів поліномів заданого степеня та функцій однієї змінної інших видів.

5.2.1 Етапи знаходження наближених значень коренів рівняння

Будь-яке рівняння з одним невідомим можна записати у вигляді

. (5.28)

Коренем рівняння (5.28) називається всяке значення змінної х, яке перетворює в нуль. Знайти точні значення коренів можливо тільки в незначній кількості випадків, для яких відомі прості формули обчислення значень коренів (наприклад, випадок квадратного і кубічного алгебраїчних рівнянь). Для рівнянь вищого степеня, трансцендентних рівнянь, рівнянь з наближеними значеннями коефіцієнтами знаходження точних значень коренів неможливе. Тому для розв’язання більшості рівнянь виду (5.28) використовують методи наближеного (чисельного) знаходження коренів рівняння, зручні для комп’ютерної реалізації. Наближеним значенням кореня х₀ з точністю до ε будемо вважати будь-яке, що міститься між числами a і b, для якого виконується умова

. (5.29)

Наприклад, якщо корінь х₀ міститься між числами 2.118 і 2.119 (тобто 2.118<х₀ <2.119), то за наближене значення кореня з точністю до 0,001 можна прийняти числа 2.338, 2.119 і будь-яке число, що міститься між ними.

Процес знаходження наближених значень коренів рівняння складається з двох етапів:

1. Відділення коренів.

2. Уточнення значень коренів до заданого степеня точності.