Лабораторна робота №7 Тема: Методи комп’ютерної обробки результатів вимірювань Завдання на лабораторну роботу:

• ознайомитися з теоретичними відомостями;

• за методом найменших квадратів виконати апроксимацію експериментальних даних, для чого вибрати вид апроксимуючої функції і визначити її параметри; сексти програму апроксимації даних і визначити середньоквадратичну помилку апроксимації;

• скласти алгоритм і програму інтерполяції експериментальних даниза методом Ньютона; обчислити значення даних в точках 3,5; 5,5; 7,5. Під час побудови інтерполяційного полінома використати експериментальні дані в інтервалі [1-8].

7.1. Апроксимація результатів вимірювань.

Експериментальне дослідження деякого процесу проводиться шляхом вимірювання кількісних значень величин, що характеризують залежність параметрів процесу від зміни умов його протікання. Результати вимірів зазвичай записуються або у вигляді таблиць, або у вигляді точок на площині з координатами x, y. Під час прийняття рішення про характер процесу за результатами експерименту може виникнути ряд проблем.

Оскількирезультати експерименту зазвичай містять похибки, то виникає задача згладжування відхилень отриманих даних, зумовлених помилками експерименту.

Може з’явитися необхідність визначити характер протікання процесу в тих точках, в яких виміри не проводилися.

Часто потрібно екстраполювати знайдену експериментальну залежність, тобто визначити її поза областю експерименту.

При випадковому спостережуваному процесі потрібно знаходити закон розподілу виміряних випадкових величин.

Перші три проблеми вирішуються шляхом апроксимації и інтерполяції отриманих експериментальних залежностей, четверта – статистичною обробкою результатів вимірювань.

Апроксимація – знаходження аналітичного виразу відомого виду, який би максимально наближав отриману експериментальну залежність. На рис. 7.1 зображена геометрична інтерпретація апроксимації.

Як видно на рис. 7.1, є ряд експериментальних точок з координатами (x_i, y_i), за якими встановлюють функціональну залежність y=φ(x). Очевидно, що під час апроксимації, насамперед, потрібно вирішити два питання:

1. Який вигляд функції вибрати для апроксимації?

2. Як провести апроксимаційну криву, щоб вона була найкращим наближенням експериментальних даних?

Рисунок 7.1. – Геометрична інтерпретація апроксимації

Зазвичай апроксимацію проводять аналітичними виразами найпростішого вигляду, наприклад степеневими многочленами, тригонометричними рядами, експоненціальними функціями тощо. Що ж стосується критерію найкращого наближення, то найчастіше користуються критерієм найменших квадратів. Цей критерій зручний з точки зору практики обчислень, оскільки він в багатьох випадках зводить проблему апроксимації до вирішення системи лінійних рівнянь. Крім того, в теорії ймовірності дається обґрунтування наступного факту: для того, щоб дана сукупність спостережуваних значень y₁,y₂,…,y_n була найімовірнішою, потрібно обрати апроксимуючу функцію φ(x) так, щоб сума квадратів відхилень спостережуваних значень y_i від φ(x) була мінімальною:

(7.1)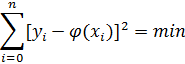

Вираз 7.1 відображає суть методу найменших квадратів. Апроксимуюча функція y=φ(x) в загальному випадку може бути записна у вигляді y=φ(x_i,a₀,a₁,…,a_i,…,a_m), оскільки вона залежить і від деяких числових параметрів a_i , що входять до неї.

Саме ці параметри потрібно визначити згідно методу найменших квадратів. Для мінімізації виразу:

(7.2)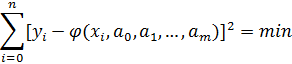

його ліву частину почергово диференціюємо по коефіцієнтах а_і і прирівнюємо до нуля. Отримуємо систему рівнянь з m невідомими, розв’язуючи її, визначаємо числові параметри а_і і тим самим знаходимо апроксимуючу функцію y=φ(x, a_і):

(7.3)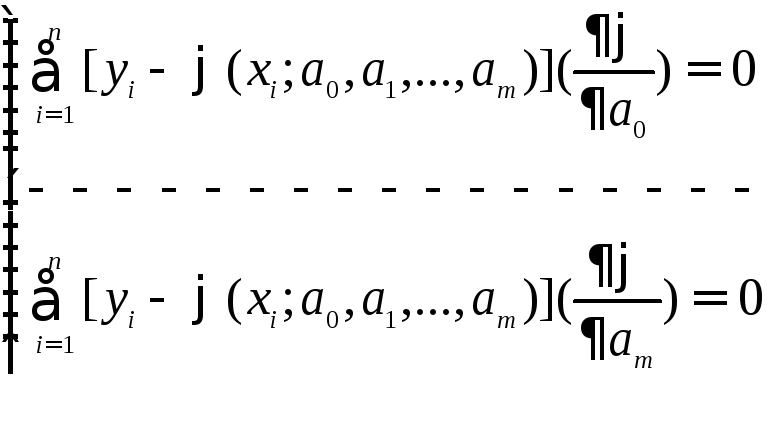

Система (7.3) записана в загальному вигляді. Для пояснення, до чого зводиться апроксимація за метод найменших квадратів з обчислювальної точки зору, розглянемо конкретний приклад.

Маємо функцію, задану в точках х_і:

Потрібно апроксимувати її поліномом другого степеня:

Визначимо коефіцієнти , використовуючи критерій найменших квадратів,

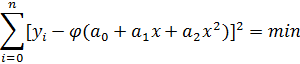
Знаходимо часткові похідні лівої частини по коофіцієнтам і прирівнюємо їх до нуля:

Розкриємо дужки и перетворимо вирази:

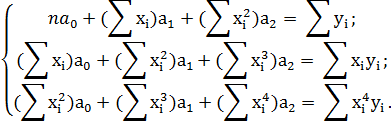
Дана система називається системою нормальних рівнянь. В загальному випадку для полінома m-ї степені система буде мати вигляд:

(7.4)

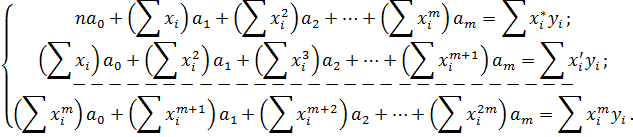
Таким чином, в обчислювальному плані задача апроксимації полягає в формуванні розширеної матриці рівнянь і її рішення за допомогою відомих чисельних методів, що розглянуті в попередніх лабораторних роботах. Вхідними даними для складення алгоритму апроксимації за методом найменших квадратів слугують масиви експериментальних даних x[n] та y[n], де (n+1) – кількість елементів в масиві; m – степінь апроксимуючого полінома.

В спрощеному вигляді алгоритм повинен складатись з чотирьох кроків: введення експериментальних даних; обчислення необхідних сум, визначення коефіцієнтів системи (6.4); рішення отриманої системи і друк результатів (числових значень коефіцієнтів поліному а_і). Більш детально алгоритм зображений на рис. 6.2. При обчисленні коефіцієнтів р_ij при невідомих (блок 6 алгоритму) використовується помічена в системі (12.4) закономірність

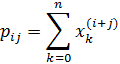
Вільні члени рівнянь обчислюються по формулі (блок 10 алгоритму)

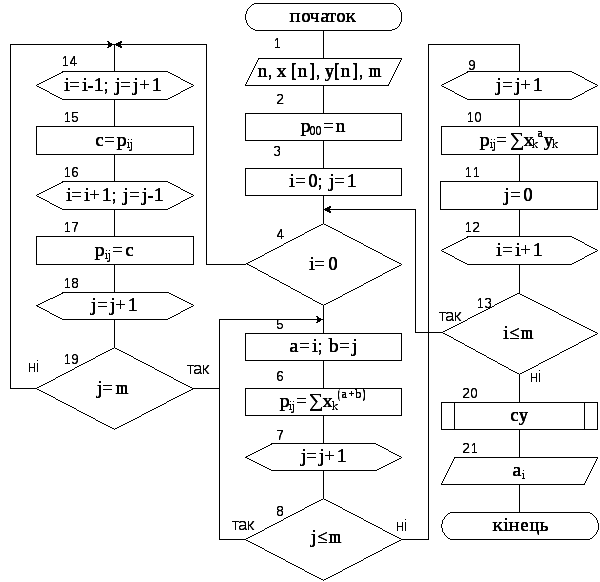
Рисунок 7.2. – Граф-схема алгоритму апроксимації експериментальних даних за методом найменших квадратів

Кількість обчислень скорочено за рахунок того, що повністю обчислюється тільки 1 стрічка, остання і передостання колонки матриці системи (блоки 4 і 13 алгоритму). Дії в блоках 1,6 і 10 представленні в спрощеному вигляді. Їх потрібно реалізувати в вигляді циклічних процесів. В алгоритмі прийняті наступні позначення:

i,j – індекси, що позначають номер стрічки и колонки відповідно; e – індекс, яким позначається номер елемента в масиві х або у; р_у – коефіцієнти, що заміняють відповідні суми в системі (12.4).