
- •Лабораторна робота №4
- •4.1.2 Метод Гауса (послідовних виключень)
- •4.1.3 Ітераційний метод Гауса - Зейделя
- •5.2 Чисельні методи знаходження коренів поліномів
- •5.2.1 Етапи знаходження наближених значень коренів рівняння
- •5.2.2 Відділення коренів рівняння
- •5.2.3 Уточнення коренів методом половинного ділення
- •Варіанти завдань на лабораторну роботу.
Лабораторна робота №4
Використання чисельних методів в комп’ютерному моделюванні
Чисельні методи розв’язання систем лінійних алгебраїчних рівнянь
і знаходження коренів поліномів
Завдання на лабораторну роботу:
• ознайомитися з теоретичними відомостями;
• розв’язати систему лінійних алгебраїчних рівнянь одним із методів;
• знайти корені заданого рівняння методом половинного ділення.
Теоретичні відомості
4.1 Чисельні методи розв’язання систем лінійних алгебраїчних рівнянь
4.1.1 Основі визначення
Системою лінійних алгебраїчних рівнянь називається система виду:
 (4.1)
(4.1)
де
![]() –
кількість невідомих.
–
кількість невідомих.
Розв’язком
системи (1) називається множина чисел
![]() ,
при підстановці яких на місце невідомих
,
при підстановці яких на місце невідомих
![]() всі
рівняння системи перетворюються в
тотожність.
всі
рівняння системи перетворюються в
тотожність.
У деяких практичних випадках система виду (1) складає задачу, яку необхідно вирішувати, в інших випадках задача зводиться до такої системи (наприклад, при апроксимації експериментальних даних деякої кривої за методом найменших квадратів) . Перш ніж приступити до розв’язання системи, її оцінюють на наявність розв’язку. Якщо при візуальному розгляді системи лінійних алгебраїчних рівнянь виявиться хоча б два рівняння з пропорційними коефіцієнтами при невідомих, то така система є виродженою (тобто має нескінченну безліч рішень або взагалі їх не має).
Відомий метод розв'язання систем лінійних алгебраїчних рівнянь за формулами Крамера критичний за обсягом обчислень до розмірності системи і практично стає неприйнятним, якщо система містить більше п'яти рівнянь. Тому з появою ЕОМ широке застосування отримали чисельні методи розв’язання таких систем. Їх можна розділити на точні (кінцеві) та ітераційні (нескінченні). Точні методи дають точне рішення (з точністю до помилок округлення) за допомогою кінцевого числа арифметичних операцій. Ітераційні методи вимагають нескінченного числа арифметичних операцій для отримання точного рішення. Тому на практиці обчислення закінчуються тоді, коли досягається прийнятна для задачі похибка, що називається похибкою обмеження. Кожен із зазначених методів має свої переваги і недоліки.
4.1.2 Метод Гауса (послідовних виключень)
Найбільш
відомим представником класу кінцевих
методів є метод Гауса. Він складається
з прямого і зворотного ходів. У процесі
прямого ходу вихідна система виду (4.1)
шляхом еквівалентних перетворень
приводиться до трикутного виду, y
зворотному ході обчислюються всі
невідомі системи, починаючи з останнього.
Для складання алгоритму розв'язання
системи
![]() -
лінійних алгебраїчних рівнянь з
-
лінійних алгебраїчних рівнянь з
![]() невідомими за методом Гауса розв’яжемо
систему з трьома невідомими і помічені
закономірності поширимо на загальний
випадок:
невідомими за методом Гауса розв’яжемо
систему з трьома невідомими і помічені
закономірності поширимо на загальний
випадок:
![]() (4.2)
(4.2)
![]() (4.3)
(4.3)
![]() (4.4)
(4.4)
Якщо![]() ,
то рівняння системи переставляємо так,
щоб в першому рівнянні коефіцієнт при
невідомому не був рівним нулю. Введемо
множники для рівнянь (4.3)
і (4.4):
,
то рівняння системи переставляємо так,
щоб в першому рівнянні коефіцієнт при
невідомому не був рівним нулю. Введемо
множники для рівнянь (4.3)
і (4.4):
![]()
Помножимо
перше рівняння системи спочатку на
![]() і
віднімемо його з рівняння (4.3), потім
помножимо перше рівняння на множник
і
віднімемо його з рівняння (4.3), потім
помножимо перше рівняння на множник
![]() і віднімемо його з рівняння (4.4). Отримаємо:
і віднімемо його з рівняння (4.4). Отримаємо:
![]() (4.5)
(4.5)
![]() (4.6)
(4.6)
Врахуємо,
що коефіцієнти при невідомому
![]() в рівняннях (4.5)
і (4.6)
дорівнюють нулю, і введемо нові позначення
коефіцієнтів при
в рівняннях (4.5)
і (4.6)
дорівнюють нулю, і введемо нові позначення
коефіцієнтів при
![]() і
і
![]() :
:
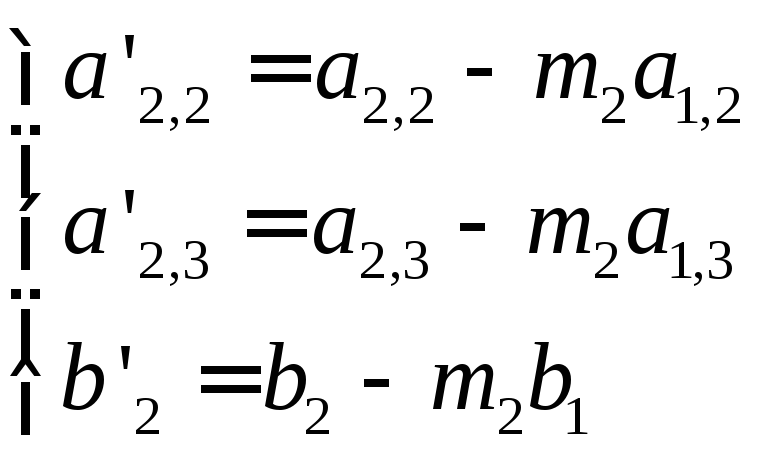 (4.7)
(4.7)
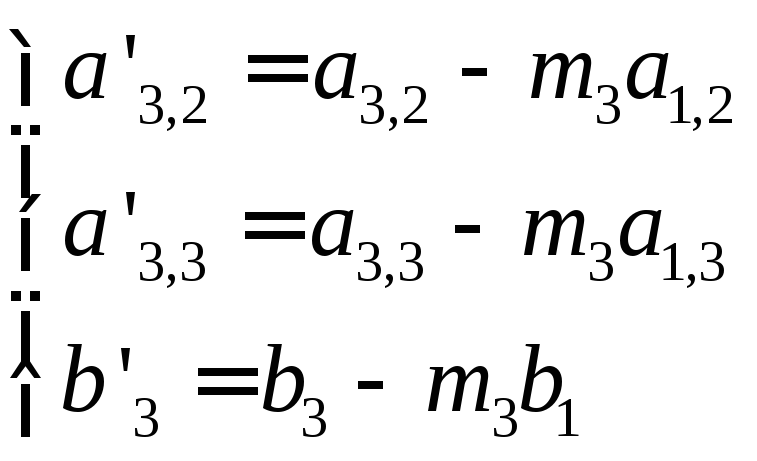 (4.8)
(4.8)
Тоді вихідну систему після виключення першого невідомого можна переписати в наступному вигляді:
![]()
![]() (4.9)
(4.9)
![]() (4.10)
(4.10)
Виключимо
таким же чином невідоме
![]() з
рівняння (4.10).
Для цього рівняння (4.9)
домножимо на множник
з
рівняння (4.10).
Для цього рівняння (4.9)
домножимо на множник
![]()
і віднімемо з рівняння (4.10). Отримаємо
![]()
де
![]() (4.11)
(4.11)
Після цього система рівнянь отримує такий вид:
![]() (4.12)
(4.12)
![]() (4.13)
(4.13)
![]() (4.14)
(4.14)
У
такому вигляді система легко вирішується.
Для цього з рівняння (4.14)
визначають
![]() ,
підставляють його значення в рівняння
(4.13)
і визначають
,
підставляють його значення в рівняння
(4.13)
і визначають
![]() ,
підставивши
,
підставивши![]() і
і
![]() в (4.12),
визначають
в (4.12),
визначають
![]() .
Цей процес зворотного ходу описується
для нашого прикладу наступними формулами:
.
Цей процес зворотного ходу описується
для нашого прикладу наступними формулами:
![]()
![]()
![]()
Як
видно, процес вирішення системи лінійних
алгебраїчних рівнянь в обчислювальному
плані зводиться до певних операцій над
коефіцієнтами розширеної матриці
системи. У загальному випадку, при
виключенні
![]() -го
невідомого з
-го
невідомого з![]() -го
рівняння системи, коефіцієнт
-го
рівняння системи, коефіцієнт![]() при
при![]() -му
невідомому і вільний член
-му
невідомому і вільний член
![]() обчислюються за наступними формулами
(див. вирази (4.7),
(4.8)
і (4.11):
обчислюються за наступними формулами
(див. вирази (4.7),
(4.8)
і (4.11):
![]() (4.15)
(4.15)
![]() (4.16)
(4.16)
де
![]() (4.17)
(4.17)
Невідомі
![]() в
процесі зворотної підстановки обчислюють
за формулою
в
процесі зворотної підстановки обчислюють
за формулою
![]() .
(4.18)
.
(4.18)
Граф-схема алгоритму розв'язання системи лінійних алгебраїчних рівнянь методом Гауса наведена на рис. 4.1.
На
граф-схемі прийнято такі позначення:
![]() -
кількість рівнянь в системі;
-
кількість рівнянь в системі;![]() -
номер невідомого, яке виключається із
решти
-
номер невідомого, яке виключається із
решти![]() рівнянь;
рівнянь;![]() -
номер рівняння, з якого в даний момент
виключається невідоме;
-
номер рівняння, з якого в даний момент
виключається невідоме;![]() -
номер
стовпця. Граф-схема точно відповідає
розібраному вище процесу, тому особливого
пояснення не вимагає.
-
номер
стовпця. Граф-схема точно відповідає
розібраному вище процесу, тому особливого
пояснення не вимагає.

Рисунок 4.1 - Граф-схема алгоритма розв’язання системи лінійних рівнянь методом Гауса
