6.2. Інтерполяція.

Досить часто при табличному заданні залежностей виникає необхідність визначення значення функції від аргументу, що відсутній в таблиці. Ця проблема вирішується інтерполяцією (знаходженням аналітичного виразу для функції, заданої таблично таким чином, щоб значення інтерполяційної функції співпадали зі всіма табличними значеннями заданої функції).

Суть інтерполювання можна наочно продемонструвати за допомогою рис. 6.3.

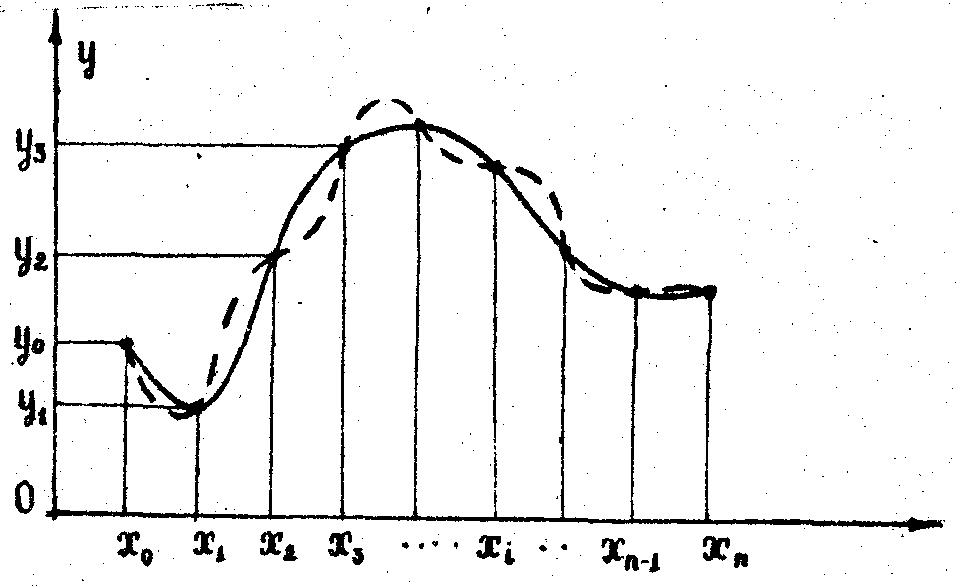
Рисунок 6.3 - Геометрична інтерпретація задачі інтерполяції

Інтерполяція, на відміну від апроксимації, передбачає збіг інтерполюючої функції з заданою у вузлах інтерполяції. Як видно з рис. 6.3, таких функцій можна отримати безліч, тому, щоб отримати єдину функцію, накладають на неї додаткові обмеження. Так, при інтерполяції поліномом, його степінь не можна обирати довільно (як при апроксимації), він повинен бути на одиницю меншою від числа вузлів інтерполяції.

Найбільш відомі методи інтерполяції – методи Лагранжа, Ньютона, Гауса та ін. Розглянемо один із них, а саме інтерполяцію для таблиць з рівним кроком зміни аргументу по інтреполюючій формулі Ньютона. При цьому, для функції, заданої таблично:

інтерполяційна функція шукається в вигляді поліному зі степенем n:

(6.5)

Поліном вважається заданим, якщо відомі коефіцієнти а_і. Їх будемо знаходити, виходячи з умови . Для цього в вираз (6.5) замість х будемо почергово підставляти значення x₀, x₁, …, x_i, … ,x_n-1.

Отримаємо

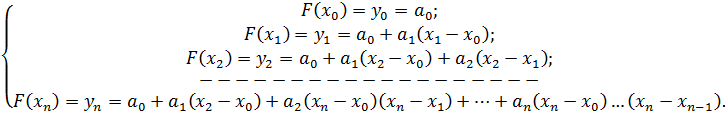
Враховуючи, що , отримуємо систему рівнянь з n невідомими (невідомі коефіцієнти поліному а_і):

Розвязавши систему, знайдемо

і т.д. В загальному випадку k-ий коефіцієнт інтерполяційного полінома знаходиться по формулі

(6.6)

і інтерполяційний поліном запишеться у вигляді

Величина називається кінцевою різницею k-го порядку і може бути обчислена через табличні значення функуції по формулі

Але в таких складних обчисленнях немає необхідності, що слідує зі з’ясування сенсу поняття «кінцева різниця». Розглянемо табл. 6.1.

Таблиця 6.1

x	y	∆y	∆2y	∆3y	∆4y	∆5y
x0	y0	∆y0	∆2y0	∆3y0	∆4y0	∆5y0
x1	y1	∆y1	∆2y1	∆3y1	∆4y1
x2	y2	∆y2	∆2y2	∆3y2
x3	y3	∆y3	∆2y3
x4	y4	∆y4
x5	y5

В 1-й і 2-й колонках таблиці записані початкові дані, в решті колонок – кінцеві різниці різних порідків, починаючи з першого і закінчуючи п’ятим. Вони обчислюються послідовно:

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

В

(6.7)

загальному випадку, і-у кінцеву різницю k-го порядку можна вичислити по рекурентній формулі

Зазвичай для інтерполяції використовують не поліном виду (12.6), а поліном, отриманий заміною змінної t=(x-x₀)/h:

(6.8)

де

(6.9)

Таким чином, знаходження інтерполюючого поліному (6.8) в обчислювальному плані зводиться до обчислення кінцевих різниць по формулі (6.7), до n-го порідяку включно, обчисленню коефіцієнтів С_k по формулі (6.9) і нокопиченню суми доданків, рівних похідним С_k∆^ky₀. Початковими даними для алгоритму інтерполювання по формулі (6.8) є масив y[n], що відповідає заданим табличним значенням функції; число елементів в масиві n; значення аргументу x, для якого знаходиться значення функції; табличний крок зміни аргументу h і початкове значення аргументу в таблиці x₀=a. Алгоритм інтерполяції зображений в вигляді граф-схеми на рис. 12.4. Крім уже вказаних, в алгоритмі використані і другі позначення: S – значення інтерполюючого полінома; d_i – і-та кінцева різниця k-го порядку; t – змінна, t=(x-x₀)/h; k – індекс коефіцієнту С і порядок кінцевох різниці.

Алгоритм містить основн кроки: введення початкових даних – блоки 1,2; задання початкових значень параметрів циклу – блок 3; обчислення кінцевих різниць – блок 4 і 6; обчислення k-го коефіцієнту С – блоки 7,8; накопичення числового значення поліному в вигляді суми S – блок 10; підготовка обчислень кінцевих різниць (k+1)-го порядку – блок 10 і 15; друк значень функції F(x) – блок 16.