§ 5. Системы линейных алгебраических уравнений

Системой линейных алгебраических уравнений, содержащей уравнений снеизвестными, называется система вида:

(5.1).

Эту систему удобно записывать в виде одного матричного уравнения

(5.2).

Здесь - матрица системы,

- вектор-столбец неизвестных,

- вектор-столбец свободных членов.

Величины , называемые коэффициентами системы, и величины, называемые свободными членами, предполагаются известными.

Система (5.1) называется однородной, если все ее свободные члены равны нулю. Если хотя бы один из свободных членов отличен от нуля, то система называется неоднородной.

Система (5.1) называется квадратной, если число уравнений равно числу неизвестных.

Решением системы (5.1) называется такая совокупность чисел, которая при подстановке в систему (5.1) на место неизвестныхобращает все уравнения системы в тождества.

Система (5.1) имеющая хотя бы одно решение, называется совместной системой. Система не имеющая решений называется несовместной.

Совместная система, имеющая единственное решение называется определенной. Система называется неопределенной, если она имеет более одного решения.

Рангом матрицы Аназывается наивысший порядок отличного от нуля минора.

Справедлива теорема Кронекера-Капелли.

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

Здесь - расширенная матрица.

Если ранг матрицы Аравен рангу расширенной матрицыи равен- числу неизвестных, то система имеет единственное решение.

Если система совместна и ранг матрицы Аменьше числа неизвестных, то система имеет множество решений.

§6. Методы решения системы линейных алгебраических уравнений

1. Матричный метод.

Пусть дана система - уравнений с- неизвестными.

Запишем систему в виде одного матричного уравнения:

(6.1).

Если определитель системы , то существует обратная матрица. Тогда, умножая (6.1) наполучим:

или.

Запишем решение системы в расширенном виде:

Рассмотрим полученные равенства:

, где

- определитель, полученный из основного определителя путем замены первого столбца столбцом свободных членов. Аналогично для всехот 2 дот.е.:

(6.2).

Формулы (6.2) носят название формул Крамера.

2. Метод Гаусса.

Суть этого метода состоит в последовательном исключении неизвестных.

Пример 9.Решить систему

Решение. Выразим из первого уравнения системы:

,

Подставим во второе и третье уравнения:

Выразим из первого уравнения полученной системы:

.

Подставим во второе уравнение:

Тогда

§7. Векторы и линейные операции над ними

Вектор – это направленный отрезок прямой, обозначается или. Точка - начало вектора, точка- его конец. Длиной или модулем вектораназывается длина отрезкаи обозначается. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается. Вектор, имеющий направление вектораи длина которого равна 1, называется единичным вектором или ортом вектораи обозначается.

Векторы иназываются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Записывается так. Два вектора называются равными, если они одинаково направлены и имеют одинаковые длины.

Три вектора в пространстве называются компланарными, если они лежат в одной или параллельных плоскостях.

Под линейными операциями над векторами понимают операцию сложения векторов и умножение вектора на действительное число.

Суммой двух векторов иназывается вектор, соединяющий начало первого векторас концом второго вектора, при условии, что начало вектораи конец векторасовмещены. Обозначается сумма. Рис.4.

Рис. 4.

Такое правило сложения векторов называется правилом треугольника. Два вектора можно сложить и по правилу параллелограмма. Рис.5.

Рис. 5.

Разность двух векторовиназывается третий вектор, такой, что. Рис.6.

Рис. 6.

Произведение вектора на числоназывается вектор, длина которого равна, он коллинеарен векторуи имеет направление вектора, если, и противоположное, если.

Линейные операции над векторами обладают следующими свойствами:

1. 

2. 

3. 

4. 

5. 

Необходимым и достаточным условием коллинеарности двух векторов иявляется существование такого числа, что.

Линейной комбинацией векторов называется сумма произведений этих векторов на действительные числа:

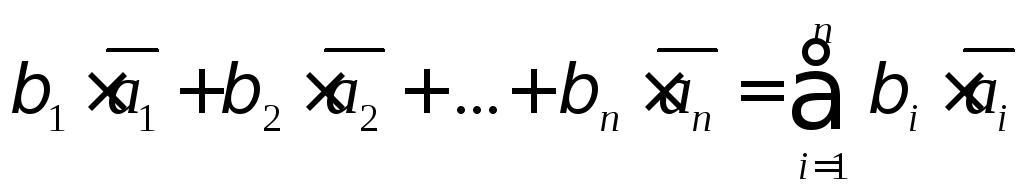(7.1).

Система векторов называется линейно независимой, если их линейная комбинация (7.1) равна нулю только при всеходновременно равных нулю.

Два вектора иобразуют базис на плоскости, если любой третий векторна плоскости можно представить в виде

(7.2).

Три вектора образуют базис в пространстве, если любой векторэтого пространства можно представить в виде:

(7.3).

Выражение (7.3) называют разложением вектора по базису из векторов, а числаназывают координатами векторав базисе. Условно это записывается.

Два неколлинеарных вектора образуют базис на плоскости, три некомпланарных вектора образуют базис в пространстве.

Если известны координаты векторов в некотором базисе, то линейные операции над векторами сводятся к обычным арифметическим операциям над координатами этих векторов.

Чтобы сложить два вектора нужно сложить их соответствующие координаты.

Чтобы найти разность двух векторов необходимо найти разность их соответствующих координат.

Чтобы умножить вектор на действительное число, необходимо умножить каждую его координату на это число.

Справедливы следующие утверждения. Два вектора равны, если равны их соответствующие координаты. Два вектора коллинеарны, если их координаты пропорциональны.

Пример 10.Даны векторы. Проверить, что векторыобразуют базис и найти координаты векторав этом базисе.

Решение. Составим линейную комбинацию векторов и приравняем ее к нулю:. Покажем, что это равенство справедливо лишь при условии. Из равенства векторов следует:

Найдем определитель полученной однородной системы:

Следовательно, система имеет единственное решение :

а это значит, что векторы - образуют базис.

Найдем координаты вектора в этом базисе.

Запишем векторное равенство:

.

Переходя к координатой форме, получим:

Решив эту систему, получим:

.

Тогда , илив базисе.

В прямоугольной системе координат любой векторможно представить в виде

(7.4),

где - взаимно ортогональные единичные векторы осей координат.

Координатами вектора в прямоугольной системе координат являются проекции этого вектора на соответствующие оси координат, то есть

(7.5).

- длина векторав прямоугольной системе координат.

Углы, которые вектор образует с осями координат, принято обозначать соответственно. Косинусы этих углов называют направляющими косинусами вектора. Направляющие косинусы равны соответственно:

(7.6),

Или в координатной форме:

.

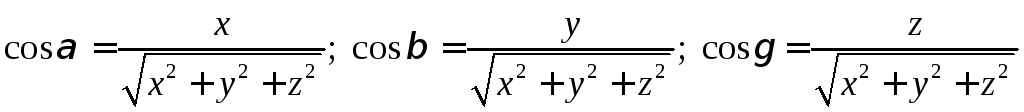Для направляющих косинусов выполняется равенство

(7.7).

Если известны координаты точек то координаты вектораопределяются формулами, то есть

.