Федеральное агентство по образованию
ГОУ ВПО
«Брянская государственная инженерно-технологическая академия»
Кафедра математики
Методические указания по выполнению расчетно-графической работы
«Линейная алгебра и аналитическая геометрия» для подготовки бакалавров по всем направлениям.
Утверждены
научно-методическим
советом академии
Протокол № __________
От _____ _________ 2011г.
Брянск 2011
§ 1. Линейные уравнения и неравенства с двумя неизвестными
Уравнением с двумя неизвестными называется выражение вида:
(1.1).
Если из уравнения (1.1) можно выразить
переменную
,
то получим уравнение вида
(1.2).
Если уравнение (1.2) имеет вид
или
(1.3),
то уравнение называют линейным, а графиком этой зависимости является прямая линия.
Из элементарной геометрии известно, что через две точки проходит единственная прямая. Это значит, что для построения прямой достаточно знать координаты двух точек, принадлежащих данной прямой.
Пример 1.Построить прямую
по ее уравнению
.
Решение.
Введем
систему координат
и определим координаты двух точек,
принадлежащих этой прямой: при
;
при
.
Нанесем эти точки на координатную
плоскость и проведем через них прямую
Рис.1.
Рис. 1.
Линейным неравенством с двумя неизвестными называют неравенство вида
, где
и
- действительные числа.
Точки плоскости
,
удовлетворяющие уравнению
(1.4) расположены на прямой, делящей всю
координатную плоскость на две полуплоскости
и
.
В одной из этих полуплоскостей выполняется
неравенство
,
в другой -
.
Пример 2.Решить неравенство
и изобразить область решения на плоскости
.
Решение. Построим прямую
Рис. 2.
Определим координаты двух точек,
принадлежащих прямой: при
;
при
.
Нанесем точки на координатную плоскость
и построим прямую, проходящую через
эти точки. Для определения области
решения неравенства, возьмем произвольную
точку плоскости, не лежащую на прямой,
например
и подставим ее координаты в заданное
неравенство:
,
т.е. неравенство не выполняется,
следовательно, областью решения заданного
неравенства служит полуплоскость, не
содержащая точку
.
Рис.2.
§ 2. Системы линейных уравнений и неравенств с двумя неизвестными
Системой двух линейных уравнений с двумя неизвестными называют совокупность двух уравнений вида:
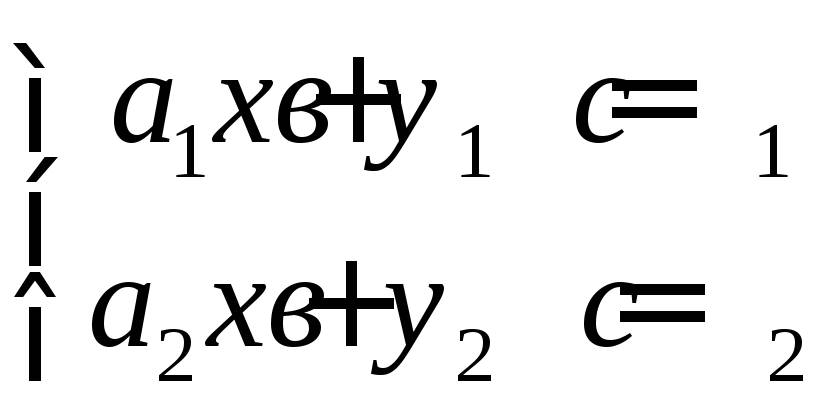(2.1).
Решением системы (2.1) называют
пару чисел 
,
удовлетворяющих каждому уравнению
системы т.е.:
.
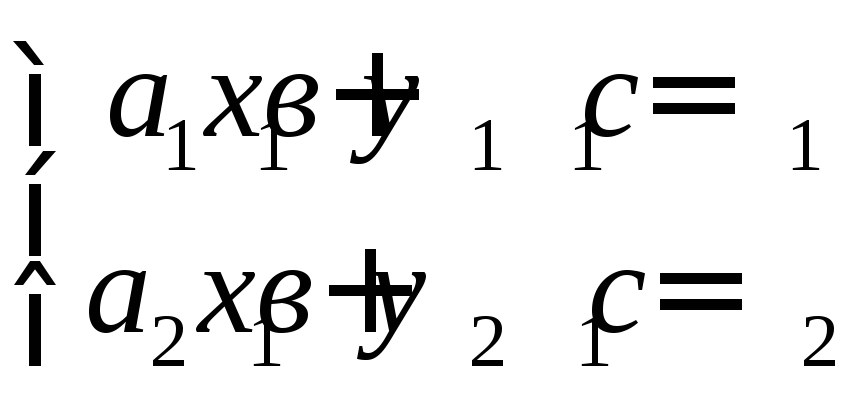Каждое уравнение системы определяет
прямую на плоскости, следовательно,
решение системы есть точка пересечения
этих прямых. Найдем координаты этой
точки. Выразим из первого уравнения
системы неизвестное
и подставим его во второе уравнение:
;
;
.
.
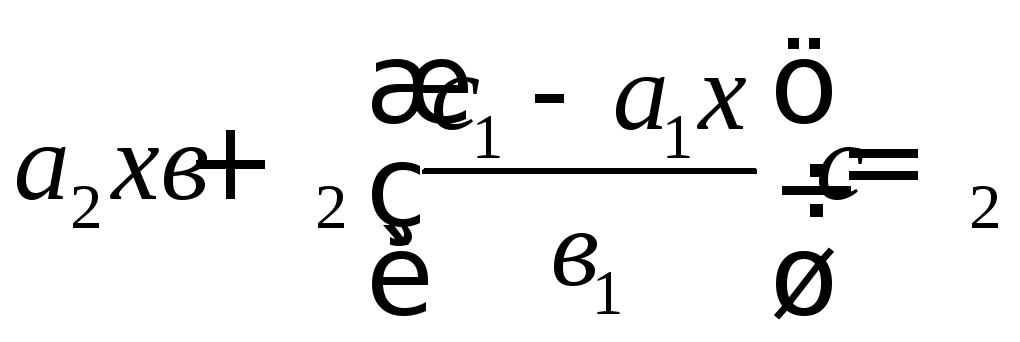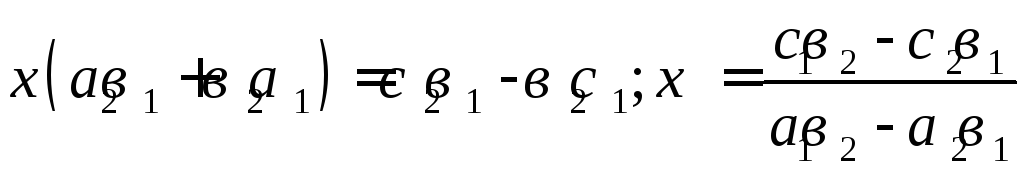Подставим значение
в выражение
,
получим: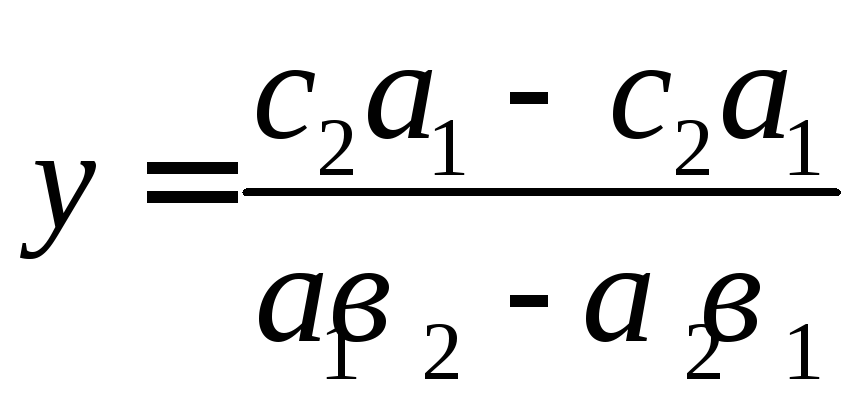
.
Введем обозначение:
.
Величину
будем называть определителем второго
порядка системы (2.1). Тогда
,
будем называть вспомогательными
определителями системы. Запишем
определители в виде таблиц, состоящих
из двух строк и двух столбцов:
.
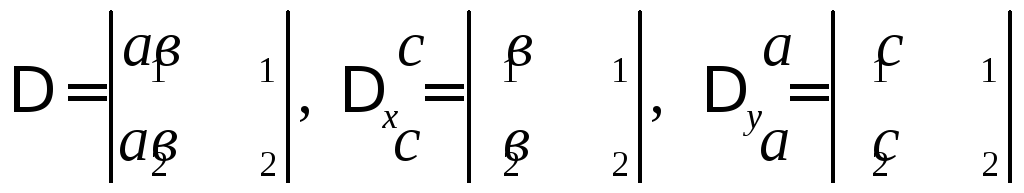Как видно, определитель системы составлен
из коэффициентов при неизвестных первого
и второго уравнений. Определители
и
получены из определителя
,
путем замены первого и второго столбцов,
соответственно, столбцом свободных
членов системы, что и оправдывает
обозначения
и
.
Очевидно, что решение системы (2.1) можно
записать в виде:
.
Пример 3.Решить систему:
.
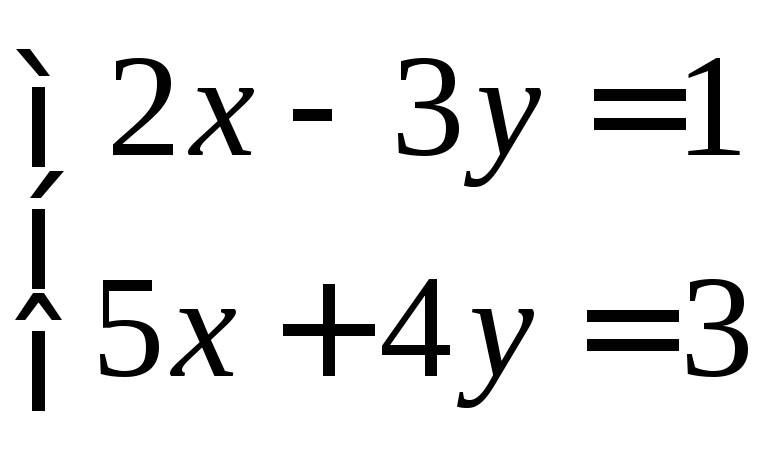Решение. Вычислим определитель
:
.
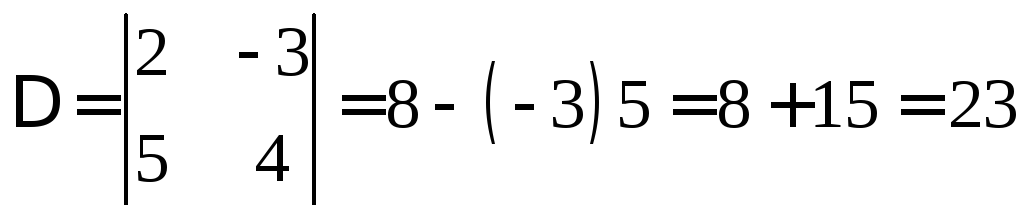Определитель
.
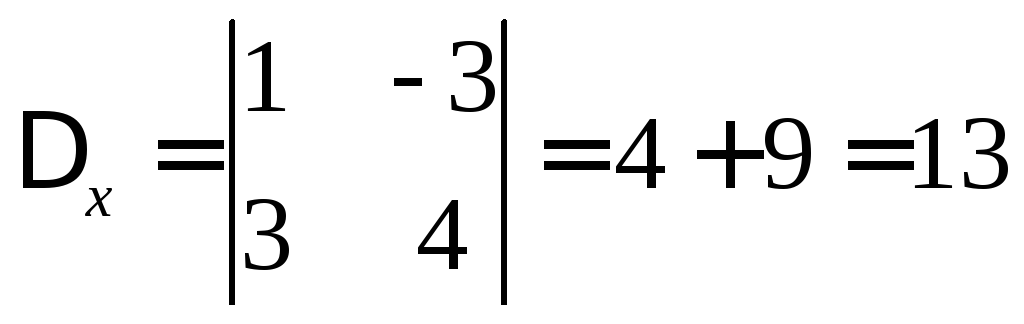Определитель
.
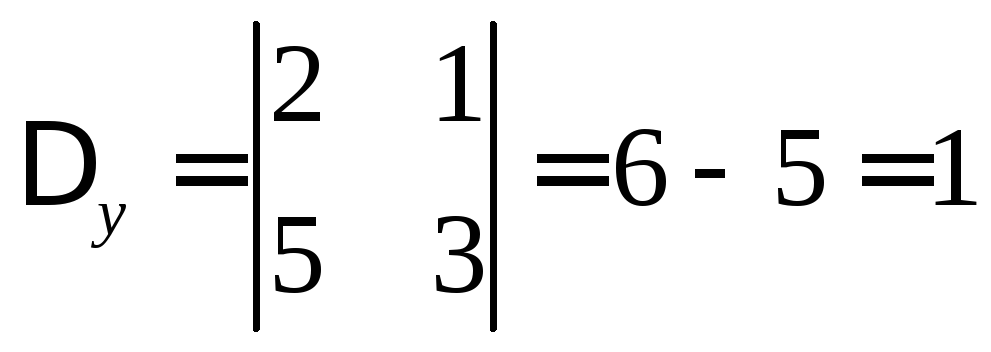Тогда: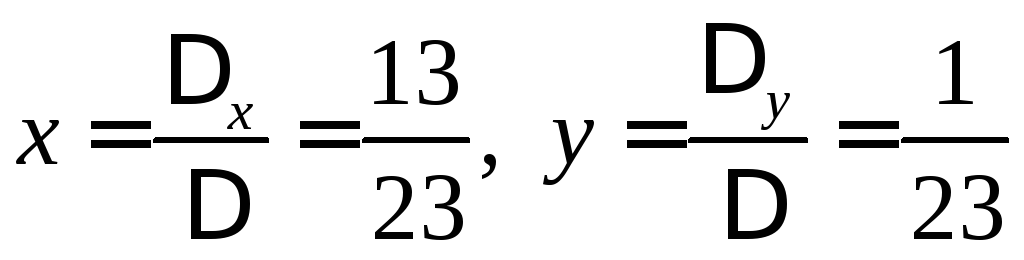
.
Ответ:
.
Система линейных неравенств с двумя неизвестными имеет вид:
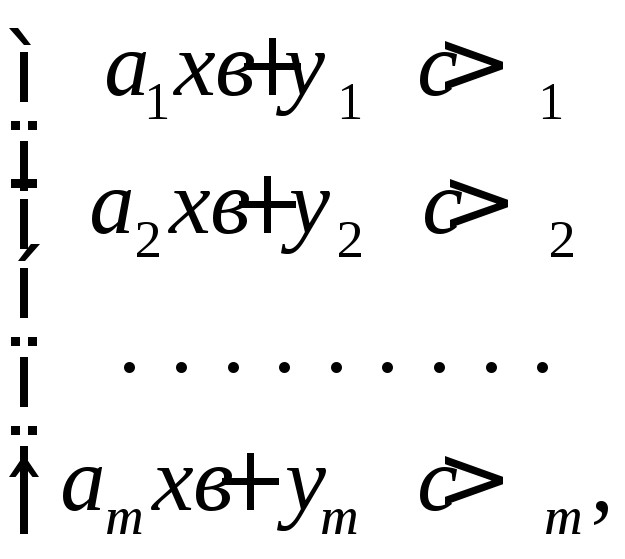(2.2)
где
- коэффициенты системы;
- свободные члены или правые части
неравенств, - действительные числа. Так
как решением каждого неравенства системы
является полуплоскость, то решением
системы служит многоугольник, координаты
точек которого удовлетворяют каждому
неравенству системы. Можно показать,
что этот многоугольник выпуклый.
Пример 4.Решить систему неравенств. Многоугольник решений изобразить на чертеже.
Решение. Найдем решение каждого неравенства системы. Заменим в каждом неравенстве знак неравенства на знак равно.
П
о
полученным уравнениям, построим прямые.
Рис.3
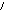
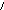
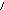
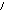
Рис. 3.
Решением служит многоугольник
.