Схемы Эйлера и Рунге-Кутта для систем уравнений

Будем считать, что задача Коши (9.2.7)  (9.2.8) имеет единственное решение на отрезкеи в дальнейшем будем называть еготочным решением этой задачи. Введём на отрезке сеткуи найдем на этой сетке приближённое решение задачи Коши. Приближённое решение представляет собой множество векторов

Каждый из этих векторов даёт приближённое значение вектор-функции в узле

.

Запишем это приближённое векторное равенство в координатах:

Абсолютная погрешность p-го компонента приближённого решения в узле представляет собой . Погрешностью всего приближённого решения (как вектор-функции) в узле сетки будем называть величину . Оценка погрешностиp-го компонента приближённого решения в узле сетки представляет собой любое положительное число , удовлетворяющее неравенству. Оценкой погрешности приближённого решения в узле сетки называется любое положительное число , удовлетворяющее неравенству.

Задача вычисления приближённого решения задачи Коши (9.2.7)  (9.2.8) с заданной точностью обычно ставится следующим образом. Для заданного положительного числа требуется подобрать сеткуи найти приближённое сеточное решение задачи Коши, абсолютная погрешность которого во всех узлах сетки не превышает заданной точности:.

Так как внешний вид задач (9.2.7)  (9.2.8), (9.1.1) почти одинаков, для приближённого решения задачи (9.2.7)  (9.2.8) строятся вычислительные схемы, аналогичные тем, которые были рассмотрены, только скалярные величины заменяются векторными. Например, схема Эйлера для приближённого решения задачи (9.2.7)  (9.2.8) будет иметь вид

, (9.2.9)

, . (9.2.10)

В координатах схема Эйлера для систем будет выглядеть более громоздко:

Аналогично строится и схема Рунге-Кутта четвертого порядка:

, (9.2.11)

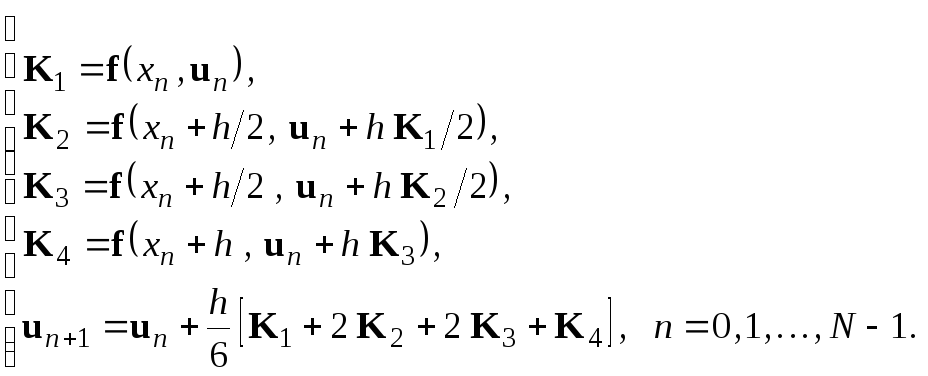(9.2.12)

Оценки погрешности вычислительных схем для векторного случая производятся так же, как и для скалярного. Можно доказать, что вычислительная схема Эйлера (9.2.9)  (9.2.10) имеет первый порядок точности, если функция f и ее частные производные непрерывны и ограничены. А вычислительная схема Рунге-Кутта (9.2.11)  (9.2.12) имеет четвёртый порядок точности, если функция f и ее частные производные до четвертого порядка непрерывны и ограничены.

Для получения приближённого решения задачи (9.2.7)  (9.2.8) с заданной точностью можно использовать правило Рунге. Строится последовательность сгущающихся (в 2 раза) сеток и для каждой пары сеток сравниваются приближённые решения на нихив совпадающих узлах . Практическая оценка погрешности приближённого решения в совпадающем узле по правилу Рунге принимает вид

. (9.2.13)

Процесс построения приближённых решений продолжается до тех пор, пока во всех совпадающих узлах двух последних сеток не будет выполнено условие

. (9.2.14)

Тогда последнее полученное приближённое решение будет иметь заданную точностьв совпадающих узлах двух последних сеток. Поскольку погрешность приближённого решения обычно принимает максимальное значение на правом конце отрезка, условие (9.2.14) обычно проверяется только при.