Оценка погрешности по правилу Рунге. Метод повторного счёта

Обычно для получения приближённых решений дифференциальных уравнений с заданной точностью используется правило Рунге (см. параграф 6.3).

Используем для приближённого решения задачи Коши (9.1.1) вычислительную схему, имеющую порядок точности k. Построим на отрезке две сетки:и. Вторую сетку получим из первой путём сгущения в 2 раза:

Тогда все узлы первой сетки будут совпадать с узлами второй сетки только с другими номерами (рис. 9.3):

.

О

Рис. 9.3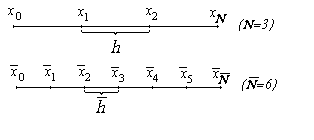

бозначимиприближённые решения, полученные на этих сетках, и сравним их с точным решением задачи Коши в совпадающих узлах. Так как, асимптотическая оценка погрешности (6.3.7) дляпримет вид

. (9.1.27)

Чтобы получить приближённое решение с заданной точностью , строится последовательность сгущающихся (в 2 раза) сеток и на каждой из них вычисляется приближённое решение. Для каждой пары сеток, в каждом совпадающем узле, проверяется выполнение неравенства

. (9.1.28)

Процесс построения сеток и приближённых решений на них продолжается до тех пор, пока условие (9.1.28) не будет выполняться во всех совпадающих узлах последней сетки. Последнее приближённое решение будет иметь заданную точность в этих узлах.

Поскольку погрешность приближённого решения обычно имеет наибольшее значение на правом конце отрезка , условие (9.1.28) нередко проверяется не во всех совпадающих узлах, а только в точке.

Многошаговые методы Методы Адамса

Рассмотренные вычислительные схемы Рунге – Кутта и Эйлера с алгоритмической точки зрения представляют собой циклы в которых последовательно вычисляются компоненты приближенного решения задачи Коши (9.1.1). Нулевой компонент определяется до начала цикла из начального условия задачи Коши (), а последующие компоненты,, …,вычисляются по рекуррентной формуле. Наn-м шаге цикла значение вычисляется по вычисленному на предыдущем шаге цикла значению(значениеn изменяется в цикле от 0 до N-1). Но если n достаточно велико, то будет вычислено ,,, …,. В этих значениях содержится дополнительная информация о точном решении задачи Коши, которую можно использовать при вычислении очередного приближенного значения. Можно ожидать, что использование полученных на предыдущих шагах цикла приближенных значений (,, …) приведет к повышению точности значения. В этом и состоит основная идея, приведшая к появлению многошаговых вычислительных схем.

Пусть имеется вычислительная схема приближенного решения задачи Коши, в которой вычисляется по вычисленным на предыдущих шагах цикла значениям,,, …,. Подобные вычислительные схемы получили названиеp-шаговых. Если p>1, то соответствующая p-шаговая схема называется многошаговой. В этой терминологии схемы Эйлера и Рунге-Кутта являются одношаговыми.

Построение многошаговых вычислительных схем сложнее, чем построение схем одношаговых. Цикл для p-шаговой вычислительной схемы начинается с . На первом шаге цикла для вычисления значениянеобходимо использовать значения,, …,. Они должны быть вычислены до основного цикла. При этом только значениеможно определить с помощью начального условия задачи Коши. Для того чтобы определить начальные компоненты приближенного решения,, …,, либо строят специальные разгонные формулы, либо используют одношаговые вычислительные схемы, например схемы Рунге-Кутта с мелким шагом, тем самым обеспечивая высокую точность этих начальных значений. Далее используется многошаговая вычислительная формула с крупным шагомh.

Н

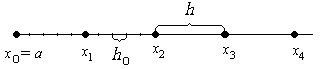Рис. 9.4

а рис. 9.4 показана сетка точек для многошаговой вычислительной схемы приp=3, . Крупно показаны узлы для многошаговой вычислительной формулы, а маленькими точками – узлы для одношаговой схемы, с помощью которой вычисляются начальные значения,,.

В дальнейшем мы не будем касаться вопроса вычисления начальных компонентов при-ближенного решения задачи Коши ,, …,, а обратимся к получению формул для вычисленияпо вычисленным на предыдущих шагах цикла значениям,,, …,.

Рассмотрим два семейства многошаговых вычислительных схем, получивших название схем Адамса. Схемы первого семейства обычно называют явными или схемами Адамса-Башфорта. Формула для вычисления вp-шаговых схемах Адамса-Башфорта имеет вид

. (9.1.29)

Если известны начальные значения ,, …,, то по явной формуле (9.1.29) последовательно и без каких-либо ухищрений вычисляются остальные компоненты приближенного решения задачи Коши:(приn=p-1), (приn=p), … , (приn=N-1). Простота использования является главным преимуществом явных схем.

Схемы второго семейства обычно называют неявными или схемами Адамса-Моултона. Формула для вычисления вp-шаговых схемах Адамса-Моултона имеет вид

. (9.1.30)

Неизвестная величина теперь находится и в левой, и в правой части равенства (9.1.30), причем под знаком функции. Решить уравнение (9.1.30) аналитически можно только для отдельных частных случаев дифференциальных уравнений (9.1.1). Для того чтобы использовать неявную схему в общем случае (для произвольного дифференциального уравнения (9.1.1)) приходится использовать для решения уравнения (9.1.30) относительноитерационные численные методы, рассмотренные в главе 2. Чаще всего используется метод простой итерации. Выбирается достаточно точное начальное приближение и проводится несколько итераций. Количество итераций обычно фиксировано и невелико, иначе схема потеряет свою вычислительную эффективность.

Несмотря на все эти неудобства, неявные схемы находят применение. Дело в том, что неявные схемы оказались менее чувствительными к вычислительным погрешностям, связанным с округлениями величин в ЭВМ, нежели явные. Все явные схемы вида (9.1.29), к которым относятся и схемы Рунге-Кутта, имеют ограничения на величину шага сетки, которых не имеют схемы неявные. Поэтому при использовании неявных схем, как правило, можно работать с более крупным шагом, не боясь разболтки. А соответственно, чем крупнее шаг сетки, тем меньше вычислительные затраты и тем быстрее будет получено приближенное решение задачи Коши. Неявные схемы могут оказаться полезными в сложных случаях, когда явные схемы работают плохо.

Рассмотрим получение многошаговых формул Адамса. Напомним, что рассматривается задача отыскания приближенного сеточного решения задачи Коши (9.1.1). Точное решение задачи Коши обозначим . На отрезкевведена сетка точекс постоянным шагом, где. Ищутся компоненты приближенного решения задачи Коши(), которые представляют собой приближенные значения. Так же как при выводе формулы Эйлера, проинтегрируем обе части дифференциального уравнения (9.1.1) на отрезкеи получим формулу (9.1.8)

.

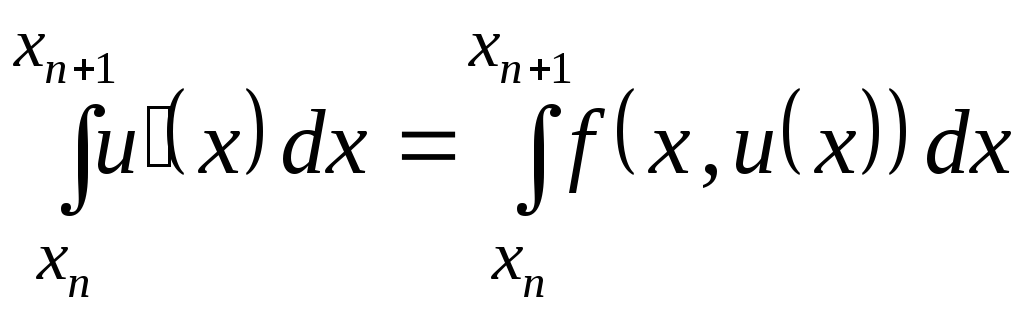Интеграл в левой части этого равенства найдем по формуле Ньютона-Лейбница

.

В результате чего получим формулу, позволяющую найти значение по известному значению:

. (9.1.31)

Будем считать, что точные значения ,, …,нам известны, и будем искать приближенное значение. Для этого построим интерполяционный многочленпо таблице значений функциив узлах,, …,

+. (9.1.32)

Кроме того, построим интерполяционный многочлен по таблице значений функциив узлах,, …,

+. (9.1.33)

Подставив в формулу (9.1.31) под знак интеграла вместо функции интерполяционный многочлен, получим первое приближенное равенство для вычисления приближенного значения

. (9.1.34)

А подставив в формулу (9.1.31) под знак интеграла вместо функции интерполяционный многочлен, получим второе приближенное равенство для вычисления приближенного значения

. (9.1.35)

Формула (9.1.34) порождает семейство формул Адамса-Башфорта, а формула (9.1.35)  семейство формул Адамса-Моултона. Получим их для некоторых значений k. При k=0 интерполяционные многочлены

, ,

а формулы (9.1.34) и (9.1.35) примут вид

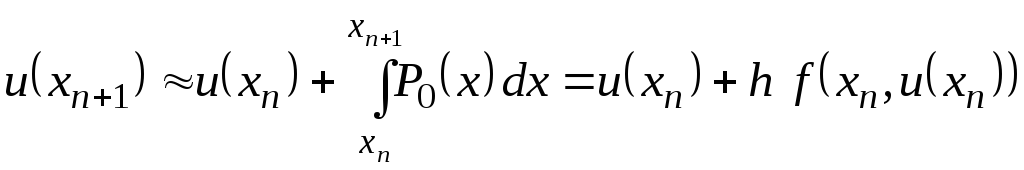, (9.1.36)

. (9.1.37)

Заменив в формулах (9.1.36) и (9.1.37) точные значения приближенными значениями, а приближенные равенства точными, получим формулу Адамса-Башфорта

(9.1.38)

и Адамса-Моултона

. (9.1.39)

При k=1 интерполяционные многочлены

,

,

а формулы (9.1.34), (9.1.35) принимают вид

, (9.1.40)

. (9.1.41)

Заменив в формулах (9.1.40), (9.1.41) точные значения приближенными значениями, а приближенные равенства точными, получим формулу Адамса-Башфорта

(9.1.42)

и Адамса-Моултона

. (9.1.43)

При k=2 аналогично получается формула Адамса-Башфорта

(9.1.44)

и формула Адамса-Моултона

. (9.1.45)

При k=3 формула Адамса-Башфорта принимаетт вид

. (9.1.46)

А формула Адамса-Моултона может быть записана в виде

. (9.1.47)

Отметим, что формулы Адамса (9.1.38), (9.1.39), (9.1.43) являются одношаговыми. Формула (9.1.38) совпадает с соответствующей формулой в вычислительной схеме Эйлера. Формулы Адамса (9.1.42), (9.1.45) являются двухшаговыми, формулы (9.1.44) и (9.1.47) – трехшаговыми, а формула (9.1.46) – четырехшаговой.

Как известно, вычислительная схема Эйлера имеет первый порядок точности. Очевидно, порядок точности вычислительных схем, основанных на формулах Адамса, зависит от порядка k используемых интерполяционных многочленов и. Конечно, он зависит и от степени гладкости функциии от порядка точности одношаговой вычислительной схемы, используемой для вычисления значений начальных компонентов приближенного решения. Можно показать, что при выполнении соответствующих условий, вычислительные схемы, основанные на формулах Адамса (9.1.38) (9.1.39), будут иметь первый порядок точности. Вычислительные схемы, основанные на формулах Адамса (9.1.42), (9.1.43), будут иметь второй порядок точности, вычислительные схемы, основанные на формулах Адамса (9.1.44), (9.1.45), будут иметь третий порядок точности, вычислительные схемы, основанные на формулах Адамса (9.1.46) и (9.1.47), будут иметь четвертый порядок точности.