
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Задание 1
- •Задание 2
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 1
- •Задание 2
- •Задание 1
- •6. Найти точное решение краевой задачи:

43
2.Повторение понятия точного и приближенного сеточного решения задачи Коши, схем Эйлера и Рунге-Кутта 4-го порядка как для одного уравнения, так и для системы уравнений.
3.Повторение многошаговых методов Адамса.
4.Повторение метода пристрелки и разностного метода решения краевых задач.
5.Решение примеров.
6.Консультирование студентов по выполнению домашней
работы.
Рассматриваемые примеры:
1. Составить алгоритм для вычисления приближённого решения задачи Коши
u′ = f ( x,u), x [a;b], u(a) =u
методом Рунге-Кутта четвертого порядка точности (число отрезков разбиения N считается заданным). Записать его на алгоритмическом языке.
Решение:
Исходными данными для алгоритма являются: N, a, b, u , а также функция f (x , u). Результаты: un - приближенные значения u( xn ) . Здесь xn = a + hn , h = (b − a) N , n = 0,1, , N .
N , n = 0,1, , N .
Вычислительная схема метода Рунге-Кутта 4-го порядка точности записывается в виде
|
|
|
|
|
|
|
u0 = |
u |
, |
|
|
||
|
|
|
|
éK1 = f ( xn ,un ) , |
|
|
|
|
|
|
|||
|
|
|
|
ê |
= f ( xn |
+ h 2, un + hK1 2) , |
|||||||
|
|
|
|
êK2 |
|||||||||
|
|
|
|
êK3 = f ( xn + h 2 , un + hK2 2) , |
|||||||||
|
|
|
|
ê |
= f ( xn |
+ h , un + hK3 ) , |
|||||||
|
|
|
|
ëK4 |
|||||||||
u |
n+1 |
= u |
n |
+ h [K + 2K |
2 |
+ 2K |
3 |
+ K |
4 |
], n = 0,1, , N −1. |
|||
|
|
6 |
1 |
|
|
|
|
||||||
Поскольку значение N может быть достаточно велико и заранее не известно, в алгоритме мы не будем использовать табличные переменные xn , un . Для текущих расчетов мы введем простые переменные x и u, а результаты будем записывать в файл вывода в следующей последовательности:
x0 u0
x1 u1
………
xN uN

44
Кроме того, мы используем в качестве результата в заголовке алгоритма величину z = uN . Нам это понадобится в дальнейшем при записи алгоритма повторного счета в примере 3. Для записи в файл значения любой величины p мы введем команду запись (p), а для перевода строки – команду перевод.
Запишем теперь алгоритм вычисления приближенного решения задачи Коши.
алг Метод Рунге-Кутта для 1 уравнения и с заданным шагом (арг вещ a, b, u , цел N, рез вещ z)
нач вещ x, u, h, K1, K 2 , K3 , K 4 ; цел n x:=a; u:= u ; h := (b − a) N ;
N ;
запись(x); запись(u); перевод | Запись в файл вывода x0 , u0 нц для n от 0 до N-1 | Начало цикла метода Рунге-Кутта.
K1 := f ( x ,u) |
| K1 := f ( xn ,un ) |
x := x +h 2 |
| x := xn + h 2 |
K2 := f ( x, u + hK1 2) |K2 := f ( xn + h
2) |K2 := f ( xn + h 2, un + hK1
2, un + hK1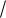 2)
2)
K3 := f ( x , u + hK2  2) | K3 := f ( xn + h
2) | K3 := f ( xn + h 2 , un + hK2
2 , un + hK2  2)
2)
x := x +h 2 |
| |
x := xn + h 2 + h 2 = xn + h = xn+1 |
K4 := f ( x , u + hK3 ) |
| |
K4 := f ( xn + h, un + hK3 ) |
u := u + h6 [K1 + 2K2 + 2K3 + K4 ]
запись(x); запись(u) | Запись в файл вывода xn+1, un+1 перевод | Переменные x и u здесь уже приняли значения,
| необходимые для выполнения следующего | шага цикла.
кц | Конец цикла метода Рунге-Кутта. z := u
кон
2. Составить алгоритм для вычисления приближённого решения задачи Коши
u′ = f ( x,u), x [a;b], u(a) =u
методом Рунге-Кутта четвертого порядка точности с погрешностью, не превышающей заданного положительного числа ε (число отрезков разбиения N вычисляется методом повторного счета). Записать его на алгоритмическом языке.
Решение:
Исходными данными для алгоритма являются: ε , a, b, u , а

также функция |
f (x , u). Результаты: un |
− приближенные значения |
u( xn ) . Здесь |
xn = a + hn , h = (b − a) N , |
n = 0,1, , N . Значение N |
вычисляется методом повторного счета. |
|
|
Метод повторного счета представляет собой цикл, в котором вычисляются приближенные сеточные решения задачи Коши. На каждом шаге этого цикла величина N увеличивается в два раза. Для записи приближенных решений мы будем использовать один и тот же файл вывода. При этом каждый раз мы будем решение записывать с начала файла. Таким образом, каждое новое приближенное решение будет автоматически стирать в файле решение старое (новое приближенное решение вдвое длиннее старого). Когда заданная точность будет достигнута и цикл повторного счета свою работу закончит, в файле будет записано последнее приближенное решение, имеющее заданную точность.
При реализации метода повторного счета мы будем использовать алгоритм из примера 1.
Введем в алгоритмический язык цикл с постусловием, аналогичный циклу repeat в языке Паскаль:
нц повторять
Команды, повторяемые в цикле кц пока не Условие окончания цикла
Запишем теперь алгоритм вычисления приближенного решения задачи Коши.
алг Метод Рунге-Кутта для 1 уравнения с автоматическим выбором шага (арг вещ a, b, u , ε )
нач вещ z1, z2 ; цел n, N
| Задание начального значения параметра N
Метод Рунге-Кутта для 1 уравнения и с заданным шагом (a,
b, u , N, z2 )
нц повторять | Начало цикла метода повторного счета z1 := z2 ; | Передача значения z2 с предыдущего шага
| цикла или начального значения. N := 2N ; | Удвоение значения параметра N.
Метод Рунге-Кутта для 1 уравнения и с заданным шагом (a, b, u , N, z2 )
кц пока не z2 − z1 ≤ ε | Конец цикла метода
15
| повторного счета
кон

46
3. Составить алгоритм для вычисления приближённого решения задачи Коши для системы дифференциальных уравнений:
ìu1′ |
= f1( x,u1 ,u2 , ,um ) , |
||
ï |
= |
f2 ( x,u1 ,u2 |
, ,um ), |
ïu2¢ |
|||
í |
|
|
x [a ,b]; |
ï............... |
|
||
ï ¢ |
|
fm ( x,u1 ,u2 , ,um ), |
|
îum = |
|||
ìu1(a) = u1 ,
ïïu2 (a) = u2 ,
í...............
ï
ïîum (a) = um
методом Рунге-Кутта четвертого порядка точности (число отрезков разбиения N считается заданным). Записать его на алгоритмическом языке.
Решение:
Исходными данными для алгоритма являются: N, m, a, b, u1 , u2 , … , um , а также функции f1( x ,u1 ,u2 , ,um ) , f2 ( x ,u1 ,u2 , ,um ) , … , fm ( x ,u1 ,u2 , ,um ) . Результаты: un p - приближенные значения u p ( xn ) . Здесь xn = a + hn , h = (b − a) N , n = 0,1, , N , p =1,2, , m .
N , n = 0,1, , N , p =1,2, , m .
Вычислительная схема метода Рунге-Кутта 4 порядка точности в координатах записывается в виде:
u0 p = u p , p =1,2, , m

47
ìéK1 p = f p (xn ,un1,un 2 , ,un m ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
ïê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ïê p = 1,2, , m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ), |
|||||||
ïêK |
2 p |
= f |
p |
(x |
n |
+ h 2, u |
n1 |
+ hK |
11 |
2 , u |
n 2 |
+ hK |
12 |
2 , ,u |
n m |
+ hK |
1m |
||||||||||||||||||||
ïê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ïê p = 1,2, , m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ïê |
K |
|
= f |
|
(x |
|
+ h 2, u |
|
+ hK |
|
2 , u |
|
+ hK |
|
2 , ,u |
|
+ hK |
|
2 ), |
||||||||||||||||||
ï |
3 p |
p |
n |
n1 |
21 |
n 2 |
22 |
n m |
2m |
||||||||||||||||||||||||||||
íê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ïê p = 1,2, , m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
), |
|
|
|
|||||||
ïêK |
4 p |
= f |
p |
(x |
n |
+ h , u |
n1 |
+ hK |
31 |
|
, u |
n 2 |
+ hK |
32 |
, , u |
n m |
+ hK |
3m |
|
|
|
||||||||||||||||
ïê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ïë p = 1,2, , m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ï |
|
|
|
|
|
|
+ h [K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
], p = 1,2, , m |
|
|
|
||||||||
ïu |
n+1 p |
= u |
n p |
1 p |
+ 2K |
2 p |
+ 2K |
3 p |
+ K |
4 p |
|
|
|
||||||||||||||||||||||||
ï |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n =0 ,1, , N −1.
Так же, как и в алгоритме из первого примера, мы не будем использовать табличные переменные xn , un p . Для текущих расчетов мы введем простую переменную x и одномерный массив u p , а результаты будем записывать в файл вывода в следующей последовательности:
x0
u01 u0 2 u0 m
x1
u11 u12 u1m
………
xN
uN 1 u N 2 u N m
Кроме того, в качестве дополнительного результата в заголовке алгоритма используем массив z [1:m], такой, что z[ p] =uN p, , p =1, 2, , m . Это может понадобиться в дальнейшем при записи алгоритма повторного счета.
Для записи в файл значения любой величины p мы введем команду запись (p), а для перевода строки – команду перевод.
Значения u p мы будем брать из файла ввода. Они должны быть записаны в файл ввода до начала исполнения алгоритма в следующей последовательности:
u 1 u 2 u m .
Для чтения очередного значения из файла ввода и присвоения
его переменной p мы введем команду чтение (p). |
|
|
|
|||
Чтобы |
описать |
множество |
функций |
fk ( x ,u1 ,u2 , ,um ) |
||
k =1,2, m c |
(m +1) аргументом, |
мы введем |
функцию |
трех |
||
аргументов: |
f (k, x,u) , |
где u = ( u1 ,u2 , ,um ) |
− |
массив |
с m |
|

48
компонентами.
Запишем теперь алгоритм вычисления приближенного решения задачи Коши.
алг Метод Рунге-Кутта для m уравнений и с заданным шагом (арг вещ a, b, цел m, цел N, рез вещ таб z[1: m])
нач вещ x, h, вещ таб u[1: m], v[1: m],
K2 [1: m], K3 [1: m], K4 [1: m]; цел n, p x:=a; h := (b − a) N ;
N ;
нц для p от 1 до m
чтение(u[ p]) ; | Чтение из файла ввода начальных
| данных: u[ p] := u0 p = |
u |
p , |
p =1,2, , m |
|
кц |
|
|
|
|
запись(x); перевод | Запись в файл вывода x0 |
||||
нц для p от 1 до m |
|
|
|
|
запись(u[ p]) | Запись в файл вывода |
u01 u0 2 u0 m |
|||
кц |
|
|
|
|
перевод |
|
|
|
|
нц для n от 0 до N-1 |
| Начало цикла метода Рунге-Кутта |
|||
нц для p от 1 до m |
|
|
|
|
K1[ p] := f ( p, x ,u) | K1 p := f p (xn ,un1, un 2 , , un m ) |
||||
кц |
| x := xn + h 2 |
|
||
x := x +h 2 |
|
|||
нц для p от 1 до m |
|
|
|
|
v[ p] := u[ p] + h × K1[ p] / 2
| |
v1 = un1 + hK11 2 , ,vm = un m +hK1m 2 |
кц |
|
нц для p от 1 до m
K 2[ p] := f ( p, x , v)
| K2 p = f p (xn +h 2, un1 + hK11
2, un1 + hK11  2 , ,un m + hK1m
2 , ,un m + hK1m  2)
2)
кц
нц для p от 1 до m
v[ p] :=u[ p] +hK 2[ p] / 2
| v1 = un1 + hK21  2 , , vm = un m + hK2m
2 , , vm = un m + hK2m  2
2
кц
нц для p от 1 до m
K 3[ p] := f ( p, x , v)
| K3 p = f p (xn +h 2, un1 + hK21
2, un1 + hK21 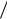 2 , ,un m + hK2 m
2 , ,un m + hK2 m  2)
2)
кц
x := x +h 2 | x := xn + h
2 | x := xn + h 2 + h
2 + h 2 = xn + h = xn+1
2 = xn + h = xn+1
49
нц для p от 1 до m
v[ p] :=u[ p] +hK 3[ p]
| v1 =un1 +hK31, , vm = un m +hK3m
кц
нц для p от 1 до m
K 4[ p] := f ( p, x , v)
| K4 p = f p (xn + h, un1 + hK31, ,un m + hK3m )
кц
запись(x); перевод | Запись в файл вывода xn+1
нц для p от 1 до m
u[ p] := u[ p] + h6 [K1[ p] + 2K 2[ p] + 2K3[ p] + K 4[ p]]
|u[ p]:= un p + h6 [K1 p + 2K2 p + 2K3 p + K4 p ] = un+1 p
запись(u[ p]) | Запись в файл вывода
| un+11 un+12 un+1m
кц
перевод | Переменная x и массив u здесь уже
| приняли значения, необходимые для | выполнения следующего шага цикла
кц | Конец цикла метода Рунге-Кутта.
нц для p от 1 до m
z[ p] :=u[ p] | z[ p] =uN p, , p =1, 2, , m
кц
кон
5. КОНТРОЛЬНАЯ РАБОТА № 2
Контрольные мероприятия по темам 4 − 5 «Численное
интегрирование. Численные методы решения обыкновенных дифференциальных уравнений и систем».
Для студентов специальности «Математическое обеспечение и администрирование информационных систем» отведено 5 часов практических занятий, а для студентов специальности «Программное обеспечение вычислительной техники и
автоматизированных систем» − 3 часа.
План занятий:
