21

n

ϕn ( x) = åαi xi лучше использовать алгоритмическую схему Горнера.

i=0

Напомним ее. Требуется для заданного значения аргумента x вычислить соответствующее значение алгебраического многочлена

n

y = åαi xi с известными коэффициентами αi . Для этого используется

i=0

циклический алгоритм:

y :=αn

нц для l от n-1 до 0 с шагом (-1)

y := yx +αl

кц

5. Дана таблица значений y j = f (x j ), ( j =1, 2 , , N ) некоторой функции y = f ( x) . Значения эти имеют значительные погрешности. Методом наименьших квадратов строится наилучшее приближение ψ( x) в семействе нелинейных функций y = axb . Составить алгоритм для вычисления коэффициентов a и b этого приближения. Определить меру близости, в смысле которой это приближение

В результате этих замен мы получим линейную зависимость:

23

Следовательно, табличные значения функции f (x) на ее периоде:

f0 = 18 , f1 = 83 , f2 = 85 , f3 = 78 .

Запишем в общем виде искомый тригонометрический интерполяционный многочлен:

S2 ( x) = a0 + a1 cos 2πLx + b1 sin 2πLx + b2 sin 4πLx .

Вычислим коэффициенты этого многочлена по формулам:

Запишем искомый тригонометрический интерполяционный многочлен

интерполяционным многочленом 2-го порядка, S2 ( x) . Найти оценку погрешности тригонометрической интерполяции.

Решение:

Функция f ( x) = sin(10π x) имеет наименьший период L =1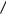5 . Порядок тригонометрического многочлена n=2. Поэтому N = 2n = 4 . Значение r может быть любым, так как функция f (x) = sin(10π x) имеет ограниченные производные любого порядка. Поэтому мы не будем конкретизировать значение r. Легко показать, что для

Подставим найденные значения в формулу оценки погрешности и получим искомую оценку погрешности тригонометрической интерполяции как функцию r:

Исследуем полученную оценку и попытаемся найти ее наименьшее значение. Величина r может иметь любое натуральное

положительного числа. Следовательно, f ( x) − S2 ( x) = 0 и S2 ( x) = f ( x) . 8. Построить для функции f ( x) = x2 ln x многочлен наилучшего

24

равномерного приближения нулевой степени, Q0f ( x) = a0f , на [0,1 ; 3].

Решение:

принадлежащей нашему отрезку. На (0,1 ; 1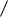e ) производная отрицательна, а на (1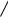e ;3) − положительна. Поэтому

на концах отрезка [0,1 ; 3]. Поэтому мы вычислим эти два значения функции и выберем наибольшее из них.

функция f (x) принимает наибольшее значение, а вторая – это точка x =1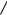e , в которой функция f (x) принимает наименьшее значение. В результате мы получим следующие равенства:

m −a0f = −E ,

M − a0f = E ,

Вычтем из второго равенства первое и выразим из получившегося равенства a0f . В результате получим искомый многочлен:

Q0f ( x) = a0f = m + M ≈ 4,58. 2

9. Построить для функции f ( x) = x2 многочлен наилучшего равномерного приближения первой степени, Q1f ( x) = a0f + a1f x , на [0 ; 1]

.

Решение:

Найдем производные нашей функции и определим характер

теореме Чебышева, на [0 ; 1] найдутся по крайней мере три точки чебышевского альтернанса для этой функции. В рассматриваемом случае две точки чебышевского альтернанса, в которых будет достигаться максимум f ( x) − a0f − a1f x , будут, очевидно, совпадать с концами отрезка [0 ;1]. Третья точка, которую мы обозначим d f и

25

в которой будет достигаться минимум f ( x) − a0f − a1f x , будет находиться внутри отрезка [0 ; 1]. В первых двух точках значение функции f ( x) − a0f − a1f x будет равно Е, а в третьей – (-Е):

f (0) − a0f = −a0f = E ,

f (1) − a0f − a1f =1− a0f − a1f = E ,

f (d f )− a0f − a1f d f = (d f )2 − a0f − a1f d f = −E .

Кроме того, в точке x = d f производная функции f ( x) − a0f − a1f x = x2 −a0f −a1f x должна обратиться в ноль:

2d f − a1f = 0.

Из полученной системы уравнений найдем искомые коэффициенты многочлена наилучшего равномерного приближения. Вычитая из первого уравнения второе, получим:

a1f =1.

Теперь из последнего уравнения можно будет найти d f :

d f = a1f .

Складывая первое и третье уравнения, получим:

(d f )2 − 2a0f − a1f d f = 0 .

Отсюда находим a0f = −18.

Осталось записать искомый многочлен: Q1f ( x) = −18 + x .

2.3. Практическая работа № 3. Численное дифференцирование. Метод Рунге-Ромберга

Для студентов специальности «Математическое обеспечение и администрирование информационных систем» отведено 4 часа практических занятий, а для студентов специальности «Программное обеспечение вычислительной техники и

автоматизированных систем» − 2 часа.

План занятий:

1. Актуализация определения производной функции одной переменной и дифференциала, его геометрического смысла, понятия бесконечно малой функции f (h) при h → 0 , сравнения

бесконечно малых функций при h → 0 , определения символа «о» − малое и «О» − большое, связь между ними, свойств символа «о» −

малое, определения верных цифр в записи приближенного значения и их свойств.