3. Пример варианта контрольной работы по теме «случайные события»

1. Победитель соревнования награждается призом (событие A), денежной премией (событие B), медалью (событие C). Что представляют собой события: а) A + B; б) ABC; в) AC – B?

2. В одной коробке находится 4 красных, 5 зелёных и 3 чёрных карандаша, а в другой – 3 красных и 2 чёрных. Из первой коробки взяты три карандаша, а из второй – два. Какова вероятность того, что все вытащенные карандаши одного цвета?

3. Из 1000 ламп 590 принадлежит 1-й партии, 200 – 2-й, остальные – 3-й партии. В 1-й партии 6%, во 2-й – 5%, в 3-й – 4% бракованных ламп. Наудачу выбирается одна лампа. Какова вероятность того, что она бракованная?

4. Определить надёжность системы:

Надёжности элементов:

Р₁ = 0,6; Р₂ = 0,8;

Р₃ = 0,5;Р₄ = 0,7;

Р₅ = 0,6.

5. Прибор содержит 2000 элементов, каждый из которых за время t может выйти из строя, независимо от других, с вероятностью 0,001. Какова вероятность выхода из строя за время t прибора, если это происходит при отказе хотя бы двух элементов?

4. Пример варианта контрольной работы по теме «случайные величины»

1. Даны законы распределения дискретных случайных величин X₁ и X₂:

Х1	-4	-3	0	3	4		Х2	-3	-1	0	1	3
Р	0,15	0,3	0,1	0,3	0,15		Р	0,1	0,2	0,4	0,2	0,1

Найти. Объяснить, почему. Построить график функции распределения случайной величины. Найти.

2. Дана функция

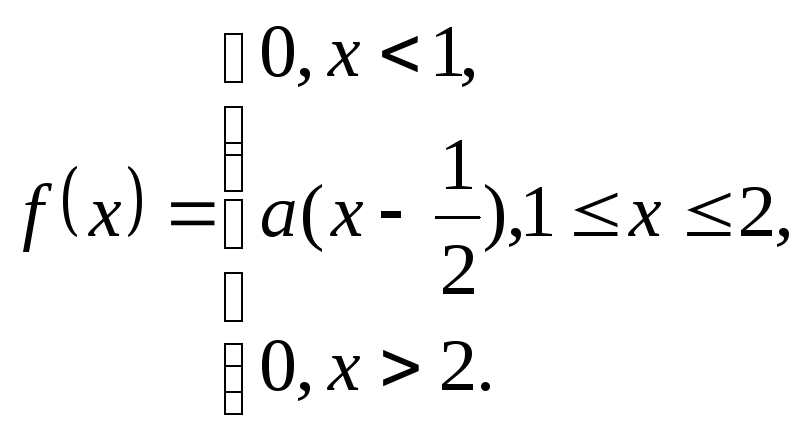
Найти .

3. Случайные ошибки измерения детали подчинены нормальному закону с параметром σ = 20 мм. Найти вероятность того, что деталь измерена с ошибкой, не превосходящей по модулю 25 мм.

4. Случайная величина X, которая равна длительности работы элемента, имеет плотность распределения 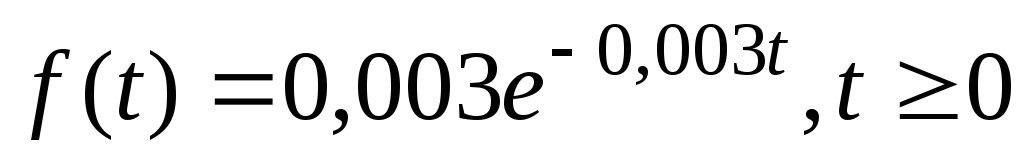. Найти среднее время работы элемента, вероятность того, что элемент проработает не менее 400 часов.

5. В урне содержится 5 белых и 3 чёрных шара. Из неё извлекают 2 шара без возвращения. Пусть случайная величина X – число белых шаров в выборке, случайная величина Y – число черных шаров в выборке. Написать закон распределения случайной величины (X, Y). Будут ли X и Y независимыми случайными величинами?

5. Вопросы к экзамену

(направления «Информатика и вычислительная техника»–профиль «ПОВТиАС», «Программная инженерия», «Математическое обеспечение и администрирование информационных систем»)

1. Классификация случайных событий. Классическое определение вероятности. Свойства вероятности события. Привести примеры.

2. Основные формулы комбинаторики.

3. Геометрическое и статистическое определения вероятности события.

4. Полная группа событий. Противоположные события. Соотношение между вероятностями событий, образующих полную группу; примеры с противоположными событиями.

5. Несовместимые и совместимые события. Сумма событий. Теорема сложения вероятностей. Привести пример на применение теоремы сложения вероятностей.

6. Зависимые и независимые события. Произведение событий. Условная вероятность. Теорема умножения вероятностей. Привести пример на применение теоремы умножения вероятностей.

7. Формулы полной вероятности и Байеса. Примеры.

8. Повторные независимые испытания. Формула Бернулли. Привести пример применения.

9. Асимптотическая формула Пуассона и условия ее применимости. Привести пример использования формулы Пуассона.

10. Локальная теорема Муавра-Лапласа и условия ее применимости. Функция Гаусса f(x) и ее свойства. Привести пример использования локальной теоремы Муавра-Лапласа.

11. Интегральная теорема Муавра-Лапласа и условия ее применимости. Функция Лапласа Φ(х) и ее свойства. Привести пример использования интегральной теоремы Муавра-Лапласа.

12. Понятие случайной величины и ее описание. Дискретная случайная величина и ее закон (ряд). Независимые случайные величины. Привести примеры.

13. Функция распределения случайной величины, ее свойства и график.

14. Математические операции над случайными величинами.

15. Математическое ожидание дискретной случайной величины и его свойства.

16. Дисперсия дискретной случайной величины и ее свойства.

17. Случайная величина, распределенная по биномиальному закону, ее математическое ожидание и дисперсия (привести пример). Закон распределения Пуассона.

18. Непрерывная случайная величина (НСВ). Вероятность отдельно взятого значения НСВ. Математическое ожидание и дисперсия НСВ.

19. Равномерно распределенная случайная величина. Случайная величина, распределенная по показательному закону.

20. Определение нормального закона распределения. Теоретико-вероятностный смысл его параметров: нормальная кривая и зависимость ее положения и формы от параметров.

21. Функция распределения нормально-распределенной случайной величины и ее выражение через функцию Лапласа Φ(х).

22. Формулы для определения вероятностей: а) попадания нормально-распределенной случайной величины в заданный интервал; б) ее отклонения от математического ожидания. Правило трех сигм.

23. Числовые характеристики случайных величин.

24. Простейшие понятия теории надежности.

25. Понятие двумерной (n-мерной) случайной величины. Функция распределения и плотности многомерной случайной величины.

26. Условные распределения составляющих многомерной случайной величины.

27. Числовые характеристики систем случайных величин.

28. Принцип практической уверенности.

29. Лемма Чебышева (неравенство Маркова). Неравенство Чебышева.

30. Теорема Чебышева и ее следствия.

31. Теорема Ляпунова и ее значение.

32. Генеральная совокупность и выборка. Статистическое распределение выборки.

33. Эмпирическая функция распределения. Выборка как набор случайных величин.

34. Генеральная и выборочная средние.

35. Генеральная и выборочная дисперсии.

36. Понятие об оценках параметров (характеристик) генеральной совокупности. Свойства оценок: несмещенность, состоятельность, эффективность.

37. Точечная оценка генеральной средней и дисперсии. Смещенность и состоятельность выборочной дисперсии. Исправленная выборочная дисперсия.

38. Понятие об интервальном оценивании. Доверительная вероятность и доверительный интервал.

39. Построение доверительного интервала для генеральной средней и среднего квадратического отклонения в случае нормально распределенного количественного признака.

40. Статистическая гипотеза. Уровень значимости.

41. Построение теоретического закона распределения по опытным данным. Понятие о критериях согласия.

42. Критерий согласия χ²-Пирсона и схема его применения.

43. Критерий согласия Колмогорова.