9.1. Элементы нейросетевого моделирования процессов в технических объектах и системах.

Нейронные сети(НС)–раздел искусственного интеллекта, для обработки сигналов в котором используются явления, аналогичные явлениям, происходящим в нейронах живых организмов.

Их важнейшей особенностью является возможность параллельной обработки информации всеми звеньями. Громадное количество межнейронных связей позволяет значительно ускорить процесс обработки информации и сделать возможным преобразование сигналов в реальном времени. Большое число межнейронных связей обеспечивает устойчивость НС к ошибкам: в этом случае функции поврежденных связей берут на себя исправные линии и деятельность сети не претерпевает существенных возмущений.

НС способны к обучению и обобщению накопленных знаний, они обладают чертами искусственного интеллекта, в частности, в обобщении полученной информации и в показании хороших результатов на не использовавшихся в процессе обучения данных

Основу каждой нейросети составляют относительно простые, в большинстве случаев – однотипные, элементы (ячейки), имитирующие работу нейронов мозга. Под нейроном будет подразумеваться искусственный нейрон, то есть ячейка нейросети.

Он обладает группой синапсов – однонаправленных входных связей, соединенных с выходами других нейронов, а также имеет аксон – выходную связь данного нейрона. Каждый синапс характеризуется величиной синаптическойсвязи или ее весом. Выход нейрона есть функция его состояния – «функция активации», или «передаточная функция» нейрона. Одним из важных факторов не является способ ее обучения. Выделяют два подхода: обучение с учителем и обучение без учителя.

Решение задач с использованием НС включает, как правило, три этапа (рис.).

В каждом из названных приложений НС играет роль универсального аппроксиматора функции от нескольких переменных, реализуя нелинейную функцию. Именно к аппроксимационному представлению могут быть сведены многие задачи моделирования, идентификации и обработки сигналов.

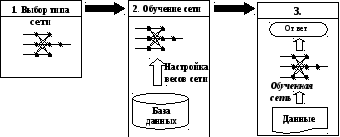
Рис. Этапы решения задачи с применением нейронных сетей

9.2. Генетические алгоритмы и их применение в моделировании технических систем.

Генетические алгоритмы (ГА)(geneticalgorithms) – большая группа методов адаптивного поиска и многопараметрической оптимизации, связанная принципами естественного отбора и генетики.

В общем случае при использовании ГА задачи оптимизации имеют следующую математическую формулировку:

найти такое значения варьируемых параметров , которые минимизируют целевую функциюпри условии, что указанные параметрыудовлетворяют допустимой области, задание которой диктуется спецификой решаемой задачи.

В качестве варьируемых параметров в этих случаях могут быть числовые коэффициенты регрессионной модели; число базисных функций; порядок уравнений регрессии; числовые коэффициенты ,,функций принадлежности; число функций принадлежности; число слоев и число нейронов в каждом слое нейронной сети.

При указанных варьируемых параметрах целевыми функциями могут быть: ошибка идентификации и прогноза в текущий или будущий момент времени; один из показателей качества процесса (функционал); ошибка обучения НС – рассогласование между выходными объекта и эталонной модели системы.

Наиболее общее определение: генетические алгоритмы(ГА) – этометоды случайного глобального поиска, копирующие механизмы естественной биологической эволюции.

Следует отметить, что существует много различных модификаций ГА. Здесь рассмотрим элементы простейшего его варианта – стандартного.

Стандартный ГА– методстохастической оптимизациидля задач дискретной оптимизации вида.

Максимизировать при условии, что.

Здесь –функция пригодности(fitnessfunction);–-мерный двоичный вектор из дискретного множества–хромосома (chromosome) илидвоичная нить(string) длины. Множество– множество вершин- мерного гиперкуба с единичным ребром;– множество действительных чисел.

Главное отличие стандартного ГА от традиционных методов оптимизации – на каждом шаге ГА имеет дело сразу с несколькими значениями вектора параметров , которые образуют популяцию (population) хромосом. В начале процедуры поиска создается начальная популяция, например, издвоичных хромосом:=, каждая из которых содержитбитов. Такая популяция создается либо случайным образом, либо с учетом априорной информации об области нахождения оптимума в множестве.

Под двоичным вектором-хромосомой понимается двоичное кодирование исходного варьируемого параметра, физический смысл которого определяется задачей. Длина хромосомы(число битов) при таком кодировании зависит от требуемой точности нахождения оптимума параметраи должна удовлетворять условию

,

где ,– предельные значения параметра;– заданная погрешность определения его оптимального значения.

Число членов в популяции влияет на широту фронта поиска и задается эмпирически.

Вычисление последующих популяций ,и т.д. на базеосуществляется путем применения трех генетических операторов:отбора(selection),кроссинговера(crossingover) имутации(mutation).

Отборв стандартном ГА реализуется методом «колеса рулетки», при котором хромосомы-кандидаты из-го поколениявыбираются для выживания в следующем,-м поколениипутем использования колеса рулетки. Каждая хромосома в популяции представлена на колесе в виде сектора с шириной, пропорциональной функции пригодности. Для отборахромосом колесо рулетки вращаютраз. В результате по завершении каждого вращения выделяется одна из хромосом, которые принимаются в качестве кандидатов в следующем поколении. Перед их копированием в новую популяцию они должны подвергнуться кроссинговеру и мутации.

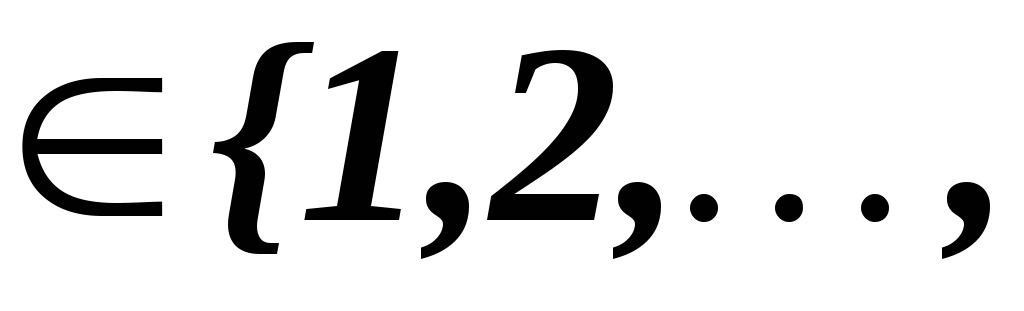
Оператор кроссинговера(скрещивания) применяется к паре хромосом из(пусть-четное), прошедших отбор.– назначаемая вероятность выполнения кроссинговера. Далее для случайно выбранной пары хромосом определяется случайное число(место или сайт кроссинговера), и затем биты из двух выбранных хромосом меняются местами после-го бита с вероятностью. Процесс повторяется до момента, когда популяцияне окажется пустой.

Оператор мутациисостоит в случайном изменении (на противоположное) значения каждого бита гена с вероятностью. Самым легким способом определения изменяемых бит (если это необходимо) – выбор независимого случайного числадля каждого бита хромосомы. Если, то-й бит следует изменить, в противном случае он сохраняется.

После мутации хромосомы-кандидаты копируются в новую популяцию хромосом и весь процесс повторяется с вычислением функции пригодности для каждой хромосомы и применением операторов отбора, кроссинговера и мутации (рис. 5.8.) [4].

Отбор методом«колеса рулетки»позволяет претендовать на выживание хромосомам с пригодностью выше среднего. Детерминированный подход по принципу выбора хромосом с наибольшей пригодностью не применяется в соответствии с допущениями генетического поиска, согласно которым даже хромосомы с низкой пригодностью могут содержать полезную инфор­мацию.

Наиболее критическим из перечисленных трех является оператор кроссинговера, так как он отвечает за смешивание информации хромосом поколение попу­ляции, а от этого зависит глобальность получаемых резу­льтатов. Установлено эмпири­чески, что .

Операторы отбора и кроссинговера используются для улучшения структуры хромосом. Цель оператора мутации – диверсификация, т.е. повышение разнообразия поиска и введение новых хромосом в популяцию для большей полноты исследования пространства поиска. Мутация инициирует разнообразие в популяции, позволяя просматривать больше точек в пространстве поиска и преодолевать локальные эксперименты в ходе поиска. Частое применение мутации приводит к разрушению хромосом с высокой приспособленностью в популяции, что сказывается на сходимости решения. Поэтому применение мутации обычно осуществляется с малой вероятностью: .

В последнее время область применения ГА значительно расширилась. Данные методы оказываются эффективными при решении следующих задач :

• идентификация сложных динамических объектов;

• выбор оптимальной конфигурации многоагентных

робототехнических систем;

• синтез оптимальных алгоритмов управления многозвенными

роботами-манипуляторами;

• оптимальное управление стыковкой космических аппаратов;

• планирование маршрутов движения транспортных средств в

условиях препятствий;

• структурный синтез проектных решений, синтез расписаний

и многих других.

Таким образом, применение ГА охватывает не только класс традиционных задач оптимизации, но и быстро распространяется на задачи управления сложными динамическими объектами в условиях неопределенности. Нельзя не отметить, что область применения ГА существенно расширилась. Одним из таких расширений является генетическое программирование (ГП), под которым понимается применение генетической модели обучения в пространстве программ. В этом случае в качестве индивидуумов, составляющих популяцию, выступают уже не указанные выше достаточно простые линейные структуры – хромосомы, а компьютерные программы, которые, будучи исполненными, представляют собой кандидатов на решение поставленной задачи.

Вопросы для самопроверки

1. Нейронные сети: их место в моделировании технологических систем

2. Роль и место генетических алгоритмов в математическом моделировании технологических систем.

3. Какую математическую формулировку имеют задачи оптимизации при использовании генетических алгоритмов?

4. В чем заключается суть стандартного генетического алгоритма для задач дискретной оптимизации?

5. В чем заключается главное отличие генетического алгоритма от традиционных методов оптимизации?

6. Что такое двоичный вектор-хромосома?

7. В чем заключается отбор методом «колеса рулетки»?

8. Дайте определение операторов «кроссинговер» и «мутация».

9. Для каких задач методы оптимизации с использованием генетических алгоритмов являются наиболее эффективными?

Рекомендуемая литература

1. Аверченков, В.И. Основы математического моделирования технических систем: учеб. пособие / В.И. Аверченков, В.П. Федоров., М.Л. Хейфец – Брянск: Изд-во БГТУ, 2004.

2. Фёдоров, В.П. Математическое моделирование в машиностроении:

учебное пособие. / В.П.Фёдоров – Брянск: БГТУ, 2013.= 112 С.