
Математика высшая
.pdf
НГАВТ - Стр 1 из 57
Е.С. Мироненко
ВЫСШАЯ МАТЕМАТИКА
Методические указания и контрольные задания для студентов-заочников инженерных специальностей высших учебных заведений
МОСКВА «ВЫСШАЯ ШКОЛА» 1998
НГАВТ - Стр 2 из 57
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ КОНТРОЛЬНЫХ РАБОТ
Цель преподавания математики в вузе — ознакомить студентов с основами математического аппарата, необходимого для решения теоретических и прак- тических задач; привить студентам умение самостоятельно изучать учебную литературу по математике и ее приложениям; развить логическое мышление и повысить общий уровень математической культуры; выработать навыка мате-
матического исследования прикладных вопросов и умение перевести задачу на математический язык.
Настоящее пособие для студентов-заочников содержит методические указа- ния и контрольные задания по курсам аналитической геометрии, линейной алгеб- ры, математического анализа, функций комплексной переменной, теория поля, числовых и функциональных рядов, дифференциальных уравнений и уравнений математической физики, теории вероятностей и математической статистики.
Всего предусматривается выполнение восьми контрольных работ, причем каждое задание содержит по 20 вариантов. Перед выполнением контрольной
работы студент должен изучить соответствующие разделы курса по учебным пособиям, рекомендуемым в данной книге. В ней же даются также некоторые начальные теоретические сведения и приводятся решения типовых примеров. Если студент испытывает затруднения в освоении теоретического или практичес- кого материала, то он может получить устную или письменную консультацию на учебно-консультационных пунктах.
Каждая контрольная работа должна быть сделана в отдельной тетради, на обложке которой студенту следует разборчиво написать свою фамилию, иници- алы и адрес, шифр, номер контрольной работы, название дисциплины я дату отправки работы в институт.
Решения задач необходимо приводить в той же последовательности, что и в условиях задач. При этом условие задачи должно быть полностью переписано перед ее решением.
Впрорецензированной зачтенной работе студент должен исправить отмечен- ные рецензентом ошибки и учесть его рекомендации и советы. Если же работа не зачтена, то ее выполняют еще раз и отправляют на повторную рецензию.
Зачтенные контрольные работы предъявляются студентом при сдаче зачета или экзамена.
Вслучае необходимости все дополнительные сведения, связанные со спецификой учебных планов данного вуза или с методикой изучения курса, принятой в этом вузе, сообщаются студентам кафедрами высшей математики вузов дополнительно к настоящему пособию.
НГАВТ - Стр 3 из 57
ЛИТЕРАТУРА
1.Беклемишев Д. В. Курс аналитической геометрия и линейной алгебры. - M.: 1987, 1998.
2.Бугров Я.С., Никольский С.М. Высшая математика. Элементы линейной алгебры а аналитической геометрии.— М.: 1980, 1984.
3.Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление.— М.: 1980, 1984.
4.Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. - М.: 1981, 1985.
5.Бугров Я.С., Никольский С.М. Высшая математика. Задачник - М.: 1982,
1987.
6.Гмурман В.Е. Теория вероятностей и математическая статистика - М.:
1997.
7.Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике.— М.: 1997.
8.Данко П.Е., Попов А.Г., Кожевникова Г.Я. Высшая математика в упражнениях и задачах (в двух частях). — М.: 1996, 1997.
9.Сборник задач по математике для втузов / Под ред. А.В. Ефимова и Б.П.
Демидовича - М.: 1986, 1987.
10.Щипачев В. С. Высшая математика - М.: 1996.
11.Щипачев В. С. Задачник по высшей математике. М.: 1998.

НГАВТ - Стр 4 из 57
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНЫМ РАБОТАМ
КОНТРОЛЬНАЯ РАБОТА № 1
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ. ЭЛЕМЕНТЫ ВЕКТОРНОЙ
И ЛИНЕЙНОЙ АЛГЕБРЫ
Основные теоретические сведения
1. Определителем (детерминантом) n-го порядка называется число D, равное алгебраической сумме n! членов, составленных определенным образом из элемен- тов определителя. Обозначение:
|
a11 |
a12 |
... |
a1n |
D = det[aij ] = |
a21 |
a22 |
... |
a2n |
|
... ... ... ... |
|||
|
an1 |
an2 |
... |
ann |
Алгебраическим дополнением Аij элемента аij определителя n-го порядка назы-
вается определитель (n - 1)-го порядка, полученный из исходного вычеркиванием i-й строки и j-го столбца и умноженный на (- 1)i+j .
Рекуррентная формула для вычисления определителя n-го порядка имеет вид
D = an1 An1 + an2 An2 + ... + ann Ann
(разложение определителя по элементам n-й строки).
Определитель второго порядка
|
|
|
|
|
|
|
|
|
|
|
D = |
a11 |
a12 |
= a |
11 |
a |
22 |
- a a |
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a21 |
a22 |
|
|
|
12 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. Скалярным |
|
|
|
произведением |
двух |
|
векторов |
ar = axi + ay j + az k и |
||||||||||||
b = bxi + by j + bzk |
называется число, определяемое равенством |
|||||||||||||||||||
v |
v |
|
v |
|
|
× |
|
b |
|
×cosϕ = axbx |
+ ayby |
+ azbz |
|
(1) |
||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
||||||||||||||||
(a,b) |
= a ×b = |
|
a |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где ϕ - угол между векторами a и b .
НГАВТ - Стр 5 из 57
r |
r |
× b |
N( A;B;C) |
с |
= a |
|
b |
|
ϕ |
М1 |
М3 |
М |
|
|
a |
2 |
|
|
|
|
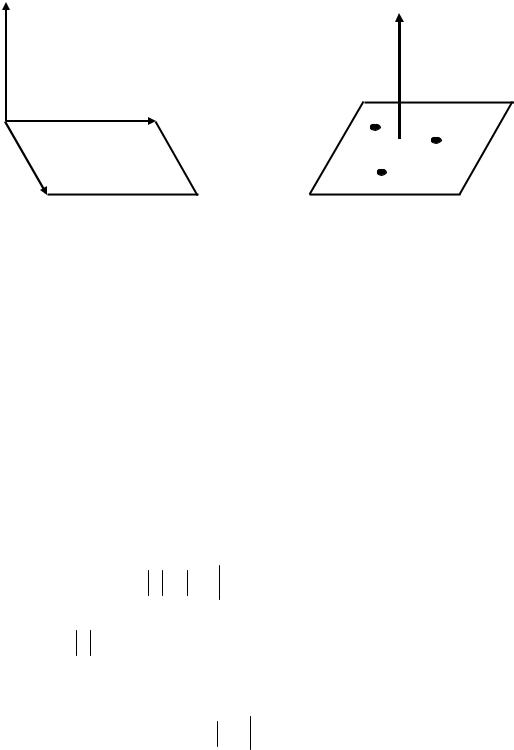
Рис. 1 |
Рис. 2 |
|
3. Векторным произведением двух векторов a и b называется вектор с , длина которого равна произведению длин векторов-сомножителей на синус угла
между ними и который направлен перпендикулярно векторам a и b так, что векторы a , b , с образуют правую тройку (рис. 1):
r |
r r |
r |
r |
= |
i |
j |
k |
= |
|
c |
= [a,b] = a |
× b |
ax |
ay |
az |
|
|||
|
|
|
|
|
bx |
by |
bz |
|
(2) |
= (ay bz − az by )i + (az bx − axbz ) j + (ax by − ay bx )k; cr = ar
 b sinϕ
b sinϕ
Геометрически c равен площади S параллелограмма, построенного на век-
торах a и b :
S = ar
 b sinϕ
b sinϕ
4. Смешанное |
произведение трех |
векторов a = axi + ay j + azk , |
b = bxi + by j + bzk , |
c =cx i + cy j + czk |
есть число, равное |

НГАВТ - Стр 6 из 57
rrr |
= |
ax |
ay |
az |
|
|
bx |
by |
bz |
(3) |
|||
abc |
||||||
|
|
сx |
сy |
сz |
|
Модуль смешанного произведения равен объему параллелепипеда, построенного
на векторах a , b , с .
5. Общее уравнение плоскости Р имеет вид
Ax + By + Cz + D = 0,
где N = Ai + Bj + Ck - нормальный вектор плоскости (рис. 2).
Уравнение плоскости, проходящей через три заданные точки М0(x0,y0,z0),
М1(x1,y1,z1), и М2(x2,y2,z2) имеет вид
x - x0 x1 - x0 x2 - x0
y - y0 y1 - y0 y2 - y0
z - z0
z1 - z0 = 0 (4) z2 - z0
|
Угол между двумя |
плоскостями, имеющими нормальные |
векторы |
|||||||||
N1 |
= A1i + B1 j + C1k и N2 |
= A2i + B2 j + C2k , определяется как угол между |
||||||||||
N1 |
и N2 ; косинус этого угла находится по формуле |
|
||||||||||
|
cosϕ = |
|
N |
× N |
|
|||||||
|
|
|
r1 |
|
|
|
r 2 |
|
|
(5) |
||
|
|
|
|
|
||||||||
|
|
|
|
|
N1 |
|
|
|
N2 |
|
|
|
6. Уравнения прямой в пространстве, проходящей через две заданные точки
М0(x0,y0,z0) и М1(x1,y1,z1) имеют вид
x - x0 |
= |
y - y0 |
= |
z - z0 |
(6) |
|
y1 - y0 |
z1 - z0 |
|||
x1 - x0 |
|
|
|||
7. Матрицей A = (aij ) размера m × n называется прямоугольная таблица чисел, состоящая из т строк и n столбцов:

НГАВТ - Стр 7 из 57
æ |
|
a |
a |
... |
a |
|
ö |
|
|
||||||
ç |
|
11 |
12 |
|
1n |
|
÷ |
ç |
|
a21 |
a22 |
... |
a2n |
|
÷ |
A = ç |
|
... |
... |
... |
... |
|
÷ |
ç |
|
|
÷ |
||||
ç |
|
am1 |
am2 |
... |
amn |
|
÷ |
è |
|
|
ø |
Произведением матрицы A = (aij ) |
размера |
m × r |
на матрицу B = (bjk ) |
размера r × n называется матрица C = AB = (cik ) |
размера m × n c элементами |
||
cik = ai1b1k + ai2b2k |
+ ... + airbrk |
(7) |
|
(поэлементное умножение i-й строки матрицы A на k-й столбец матрицы B). Матрица размера n × n называется квадратной матрицей n-го порядка. Эле-
менты a11,a22 ,...,ann образуют главную диагональ матрицы. Определитель, составленный из элементов квадратной матрицы, называется определителем мат-
рицы н обозначается A или det A.
|
|
|
|
aij = |
ì1 |
при i = j |
|
|||||||||
Матрица |
Е |
с |
элементами |
í |
при i ¹ j называется |
единичной |
||||||||||
|
|
|
|
|
|
0 |
||||||||||
матрицей n-го порядка. |
|
|
|
|
|
|
î |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Матрица A−1 |
называется обратной к матрице A(det A ¹ 0), если |
|
||||||||||||||
|
|
|
A−1 A = AA−1 = E |
|
|
|
|
|
(8) |
|||||||
Элементы aij−1 |
обратной матрицы A−1 = (aij−1) |
вычисляются по формулам |
||||||||||||||
|
|
|
aij−1 = |
|
|
Aij |
|
|
, |
|
|
|
|
|
(9) |
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Aij - алгебраическое дополнение элемента aij , матрицы A , а |
|
A |
|
- |
ее опреде- |
|||||||||||
|
|
|||||||||||||||
литель. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. Матрица Ar |
называется канонической, |
если в начале ее главной диагонали |
||||||||||||||
стоят единицы, а все остальные элементы равны нулю; например,
НГАВТ - Стр 8 из 57
æ |
1 |
0 |
0 |
0 |
ö |
ç |
0 |
1 |
0 |
0 |
÷ |
ç |
÷ |
||||
A = ç |
0 |
0 |
1 |
0 |
÷ |
ç |
÷ |
||||
ç |
0 |
0 |
0 |
0 |
÷ |
è |
ø |
Любая матрица А может быть приведена к каноническому виду Ar путем элементарных преобразований: а) перестановки столбцов (строк); б) умножения столбца (строки) на число, отличное от нуля; в) прибавления к элементам какого- либо столбца (строки) соответствующих элементов другого столбца (строки), умноженных на число.
Матрицы, переходящие друг в друга в результате элементарных преобразова-
ний, называются эквивалентными: A ~ Ar .
Число г единиц, стоящих на главной диагонали канонической матрицы Ar не
зависит от способа приведения матрицы А к каноническому виду и называется рангом исходной матрицы A: r(A)=r. Эквивалентные матрицы имеют один и тот же ранг.
9. Система трех линейных уравнений с тремя неизвестными х1, х2,
х3 имеет вид
ìа х + а х |
2 |
+ а х |
3 |
= b , |
|
|||||||
ï |
11 |
1 |
|
12 |
|
13 |
|
1 |
|
|||
íа21 |
х1 |
+ а22 |
х2 |
+ а23 |
х3 |
= b2 , |
(10) |
|||||
ïа |
31 |
х + а |
32 |
х |
2 |
+ а |
33 |
х |
3 |
= b , |
|
|
î |
1 |
|
|
|
|
3 |
|
|||||
где аij - коэффициенты системы; bi - свободные члены. Определитель третьего
порядка |
, составленный из коэффициентов при неизвестных, называется |
|
определителем системы. Если D ¹ 0, то единственное решение системы (10) |
||
выражается формулами Крамера: |
|
|
|
x1 = D1 / D; x2 = D2 / D; x3 = D3 / D, |
(11) |
где D1, D2 , D3 - определители третьего порядка, получаемые из |
определителя |
|
системы |
заменой 1, 2 или 3-го столбца соответственно свободными членами |
|
b1, b2 , b3 . |
|
|
Систему (10) можно записать матричной форме: AX = B , где |
|
|
НГАВТ - Стр 9 из 57
æ a |
11 |
a |
12 |
ç |
|
||
A = ça |
21 |
a22 |
|
ç |
|
a32 |
|
è a31 |
|||
a13 ö÷ a23 ÷, a33 ÷ø
æ x |
|
ö |
æ b |
ö |
ç |
1 |
÷ |
ç 1 |
÷ |
X = ç x2 |
÷, |
B = çb2 |
÷. |
|
ç x |
3 |
÷ |
çb |
÷ |
è |
ø |
è 3 |
ø |
|
Тогда ее решение имеет вид
X = A−1B, |
(12) |
если определитель системы отличен от нуля.
Если система линейных уравнений с n неизвестными совместна, а ранг матрицы системы меньше числа неизвестных, т. е.
r < n |
(13) |
то система имеет бесконечное множество решений. Свободные n – r неизвестных выбираются произвольно, а главные r неизвестных определяются единственным образом через свободные неизвестные.
9. Вектор-столбец
æ x |
ö |
|
ç 1 |
÷ |
|
ç x2 |
÷ |
|
ç . |
÷ |
¹ 0 |
X = ç |
÷ |
|
ç . |
÷ |
|
ç |
÷ |
|
ç . |
÷ |
|
ç |
÷ |
|
è xn |
ø |
|
называется собственным вектором квадратной матрицы А п-го порядка, со- ответствующим собственному значению λ, если он удовлетворяет матричному
уравнению
АХ=λХ, или (А - λЕ)Х = 0
Здесь Е - единичная матрица n-го порядка, а 0 - нулевой вектор-столбец. При условии, что вектор Х¹О, получаем характеристическое уравнение для определе-
ния собственных значений λ: |
|
det(A − λE) = 0 |
(14) |
Координаты собственного вектора Xi соответствующего собственному зна- чению λi, являются решением системы уравнений

НГАВТ - Стр 10 из 57
ì (a11 - λ1)x1 + a12 x2 + ... + a1n xn = 0 |
|
||||||||||||||
ïa |
x + (a |
22 |
- λ )x |
2 |
+... + a |
2n |
x |
n |
= 0 |
|
|||||
ï |
21 1 |
|
|
2 |
|
|
|
|
|
(15) |
|||||
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï ................................................. |
|
||||||||||||||
ïa x + a |
n2 |
x |
2 |
+... + (a |
nn |
- λ )x |
n |
= 0 |
|
||||||
î n1 1 |
|
|
|
|
n |
|
|
|
|||||||
Собственный вектор определяется с точностью до постоянного множителя. Пример 1. По координатам вершин пирамиды А1 (3; -2; 2), А2 (1; —3; 1), A3 (2;
0; 4), А4 (6; -4; 6) найти: 1) длины ребер А1Аг и А1А3; 2) угол между ребрами А1Аг и А1А3; 3) площадь грани А1АгА3 ; 4) объем пирамиды
Решение. 1) Находим векторы А1Аг и А1А3:
A1 A2 = (1- 3)i + (-3 - (-2)) j + (1- 2)k = -2i - j - k ;
A1 A3 = (2 - 3)i + (0 - (-2)) j + (4 - 2)k = -i + 2 j + 2k.
Длины этих векторов, т. е. длины ребер А1Аг и А1А3, таковы:
A1 A2 = 
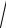 (-2)2 + (-1)2 + (-1)2 =
(-2)2 + (-1)2 + (-1)2 = 
 6;
6;
A1 A3 = 
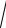 (-1)2 + 22 + 22 = 3.
(-1)2 + 22 + 22 = 3.
2) Скалярное произведение векторов A1 A2 и A1 A3 находим по формуле (1):
A1 A2 × A1 A3 = (-2)×(-1) + (-1) ×2 + (-1) ×2 = -2,
а косинус угла между ними — по формуле (5):
cosφ = |
|
A1 A2 |
× A1 A3 |
= |
- 2 |
|
= -0,27 |
|||
|
|
|
|
|
|
|||||
|
|
A1 A2 |
|
A1 A3 |
|
|
3 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда следует, что φ — тупой угол, равный π − arccos 0,27 = 1,85 рад с точ- ностью до 0,01. Это и есть искомый угол между ребрами А1Аг и А1А3.
3) Площадь грани А1АгА3 равна половине площади параллелограмма, по-
строенного на векторах и A1 A3 , т. е. половине модуля векторного произведения этих векторов [см. формулу (2)]:
